
- •Теоретические сведения
- •Практическая часть
- •Варианты заданий Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 7
- •Вариант 8
- •Вариант 9
- •Вариант 10
- •Среди трехмерных выделяют
- •5. Построение графиков поверхностей
- •6. Форматирование графика поверхности.
- •Тема 3: Численные методы решения нелинейных уравнений и оптимизация функций.
- •Теоретические сведения.
- •Метод простых итераций.
- •Метод Ньютона.
- •Средства пакета MathCad для решения нелинейных уравнений
- •2. Решение систем нелинейных уравнений. Метод простых итераций (последовательных приближений).
- •Средства пакета MathCad для решения нелинейных уравнений
- •Функции MathCad для решения задач оптимизации.
- •Варианты заданий
- •Вариант 9
- •Вариант 10
Варианты заданий Вариант 1
1)
Вычислить
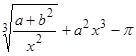 ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
2)
Используя переменную типа «дискретный
аргумент», задать
.
2)
Используя переменную типа «дискретный
аргумент», задать![]() элементы
вектора
элементы
вектора
![]() по
правилу
по
правилу
![]() ,
если
,
если
![]() .
3)
Ввести с клавиатуры векторы
.
3)
Ввести с клавиатуры векторы
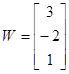 ,
,
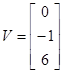 .,
матрицы
.,
матрицы
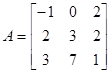 ,
,
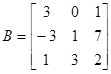 .
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
.
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
г)
сумму элементов каждой строки матрицы
;
г)
сумму элементов каждой строки матрицы
![]() .
4)
Решить систему уравнений
.
4)
Решить систему уравнений
![]() с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
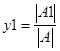 ,
где
,
где
![]() –
матрица, полученная из матрицы
–
матрица, полученная из матрицы
![]() заменой
первого столбца вектором
заменой
первого столбца вектором
![]() .
6)
Вычислить
.
6)
Вычислить
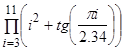
Вариант 2
1)
Вычислить
![]() ,
где
,
где
![]() ,
,
![]() ,
,
![]() .
2)
Используя переменную типа «дискретный
аргумент», задать
.
2)
Используя переменную типа «дискретный
аргумент», задать![]() элементы
вектора
элементы
вектора![]() по
правилу
по
правилу
![]() ,
если
,
если
![]() .
3)
Ввести с клавиатуры векторы
.
3)
Ввести с клавиатуры векторы
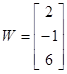 ,
,
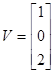 и
матрицы
и
матрицы
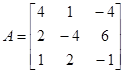 ,
,
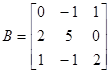 .
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
.
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
г)
сумму элементов каждой строки матрицы
;
г)
сумму элементов каждой строки матрицы
![]() .
.
-
Решить систему уравнений
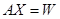 с
помощью обратной матрицы и с помощью
функции lsolve.
с
помощью обратной матрицы и с помощью
функции lsolve.
-
Найти число
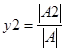 ,
где
,
где
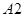 –
матрица, полученная из матрицы
–
матрица, полученная из матрицы
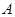 заменой
второго столбца вектором
заменой
второго столбца вектором
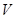 .
.
-
Вычислить
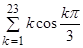 .
.
Вариант 3
1)
Вычислить
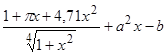 ,
где
,
где
![]() .
.
![]() ,
,
![]() .
2)
Используя переменную типа «дискретный
аргумент», задать
.
2)
Используя переменную типа «дискретный
аргумент», задать![]() элементы
вектора
элементы
вектора
![]() по
правилу
по
правилу
![]() ,
если
,
если
![]() .
3)
Ввести с клавиатуры векторы
.
3)
Ввести с клавиатуры векторы
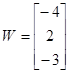 ,
,
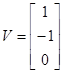 и
матрицы
и
матрицы
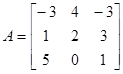 ,
,
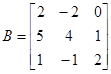 .
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
.
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
г)
сумму элементов каждой строки матрицы
;
г)
сумму элементов каждой строки матрицы
![]() .
4)
Решить систему уравнений
.
4)
Решить систему уравнений
![]() с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
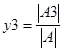 ,
где
,
где
![]() –
матрица, полученная из матрицы
–
матрица, полученная из матрицы
![]() заменой
третьего столбца вектором
заменой
третьего столбца вектором
![]() .
6)
Вычислить
.
6)
Вычислить
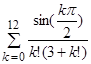 .
.
Вариант 4
1)
Вычислить
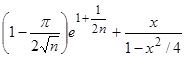 ,
где
,
где
![]() ,
,
![]() .
2)
Используя переменную типа «дискретный
аргумент», задать
.
2)
Используя переменную типа «дискретный
аргумент», задать![]() элементы
вектора
элементы
вектора![]() по
правилу
по
правилу
![]() ,
если
,
если
![]() .
3)
Ввести с клавиатуры векторы
.
3)
Ввести с клавиатуры векторы
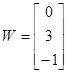 ,
,
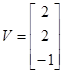 и
матрицы
и
матрицы
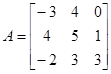 ,
,
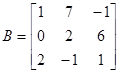 .
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
.
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
г)
сумму элементов каждой строки матрицы
;
г)
сумму элементов каждой строки матрицы
![]() .
4)
Решить систему уравнений
.
4)
Решить систему уравнений
![]() с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
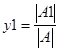 ,
где
,
где
![]() –
матрица, полученная из матрицы
–
матрица, полученная из матрицы
![]() заменой
первого столбца вектором
заменой
первого столбца вектором
![]() .
6)
Вычислить
.
6)
Вычислить
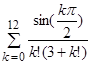 .
.
Вариант 5
1)
Вычислить
![]() ,
где
,
где
![]() ,
,
![]() .
2)
Используя переменную типа «дискретный
аргумент», задать
.
2)
Используя переменную типа «дискретный
аргумент», задать![]() элементы
вектора
элементы
вектора
![]() по
правилу
по
правилу
![]() ,
если
,
если
![]() .
3)
Ввести с клавиатуры векторы
.
3)
Ввести с клавиатуры векторы
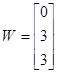 ,
,
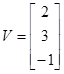 и
матрицы
и
матрицы
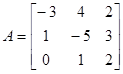 ,
,
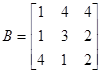 .
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
.
Вычислить:
а)
скалярное и векторное произведение
векторов W
и V;
б)
сумму элементов данных векторов;
в)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
г)
сумму элементов каждой строки матрицы
;
г)
сумму элементов каждой строки матрицы
![]() .
4)
Решить систему уравнений
.
4)
Решить систему уравнений
![]() с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
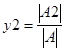 ,
где
,
где
![]() –
матрица, полученная из матрицы
–
матрица, полученная из матрицы
![]() заменой
второго столбца вектором
заменой
второго столбца вектором
![]() .
6)
Вычислить
.
6)
Вычислить
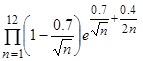 .
.
Вариант 6
1)
Вычислить
![]() где
где
![]() ,
,
![]() .
2)
Используя переменную типа «дискретный
аргумент», задать
.
2)
Используя переменную типа «дискретный
аргумент», задать![]() элементы
вектора
элементы
вектора![]() по
правилу
по
правилу
![]() ,
если
,
если
![]() .
3)
Ввести с клавиатуры векторы
.
3)
Ввести с клавиатуры векторы
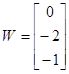 ,
,
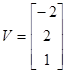 и
матрицы
и
матрицы
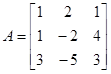 ,
,
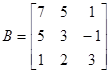 .
Вычислить:
а)
скалярное и векторное произведение
векторов W и V;
б) сумму элементов данных
векторов;
в)
.
Вычислить:
а)
скалярное и векторное произведение
векторов W и V;
б) сумму элементов данных
векторов;
в)
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ;
г)
сумму элементов каждой строки матрицы
;
г)
сумму элементов каждой строки матрицы
![]() .
4)
Решить систему уравнений
.
4)
Решить систему уравнений
![]() с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
с
помощью обратной матрицы и с помощью
функции lsolve.
5)
Найти число
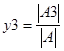 ,
где
,
где
![]() –
матрица, полученная из матрицы
–
матрица, полученная из матрицы
![]() заменой
третьего столбца вектором
заменой
третьего столбца вектором
![]() .
6)
Вычислить
.
6)
Вычислить
![]() .
.
