Лист n°2 Динамическое исследование механизма
И
сходные
данные:
т2 = 210 кг
т3 = 80 кг
т4 =160 кг
т5 = 40 м
=
0,175 mi
Li
РС = 2900 Н
1. Кинетостатический расчет механизмов методом планов сил
Составим схему нагружения механизма внешними силами и силами инерции.
Определим силы тяжести по величине:
G2
= m2
g
= 210 
9,8 ≈
2100H
, G3
=
m3
g
= 80 
9,8 ≈800H
G4
= m4
g
=
160 
9.8
≈
1600H,
G5
=
m5
g
= 40 
9,8
≈400H
.
По условию задачи звено АВ вращается с постоянной угловой скоростью, и центр тяжести звена совпадает с осью вращения, поэтому инерционная нагрузка этого звена будет равна нулю:
Звено
ВС (шатун) совершает плоскопараллельное
движение, при этом возникают силы
инерции
210
219
= 13140 H
направленная
противоположно ускорению aS2
центра тяжести и приложенная в точке
S2,
в момент инерции
=
4,2
133,6
= 575,4
Н
м
направленный
противоположно угловому ускорению
звена АВ.
Для
удобства силового расчета механизма
момент инерции
представляем
эквивалентной парой сил:
Звено
CD
(коромысло) совершает возвратно-вращательное
движение, в этом случае также имеет
место сила инерции
и
момент
.
Определяем силу инерции:
=
m3
=
80 
143,3
= 30093 H
=
0,4
263,4
= 105,2
Н
м
Заменяем
эквивалентной парой сил на плече CD.
Определяем величины сил пары:
Звено EF (шатун) совершает плоскопараллельное движение. Определяем возникающие при его движении силу инерции и момент инерции:
=
= 190 
198
= 37620 H
=
5,4
53
= 286,2
Н м
Силу инерции РИ4 прикладываем в точке S4 в сторону, противоположную ускорению aS4, момент инерции заменяем эквивалентной парой сил:
Звено 5 (ползун) совершает поступательное движение вдоль неподвижной направляющей. В этом случае возникает только сила инерции
=
40 
171,7
= 10116 H
Силовой
расчет механизма начинаем с наиболее
удаленной от ведущего звена группы 4 –
5, состоящей из звеньев 4 и 5. На группу
4
– 5
действуют известные по величине и
направлению силы G4,
С5,
,
,
,
и
Рп с . Освобождаем группу 4 –
5
от связей и прикладываем вместо них
две реакции: одну реакцию
–
в поступательной паре F,
перпендикулярную к направляющей ползуна
и неизвестную по величине (направление
R05
принимается
перпендикулярным
к направляющей в условиях, когда силы
трения не учитываются); другую
–
в шарнире Е, неизвестную по величине и
направлению. Реакцию
представляем
в виде двух составляющих: тангенциальной
,
направленной перпендикулярно к оси
звена EF,
и нормальной
,
направленной вдоль звена EF.
Направлением составляющих задаемся
произвольно. Чтобы определить реакции
в кинематических парах F
и G,
составляем векторное уравнение
равновесия сил, действующих на группу
4
– 5,
причем сначала в уравнение записываем
все силы, действующие на звено 4, затем
на звено 5:
Реакцию
входящую в уравнение, можно определить
аналитически, - для этого составляем
уравнение моментов всех сил, действующих
на звено EF,
относительно точки F
;
откуда
Для
построения плана сил, исходя из величин
сил, входящих в уравнение, задаемся
масштабом плана
и
вычисляем длины векторов, изображающих
известные силы:
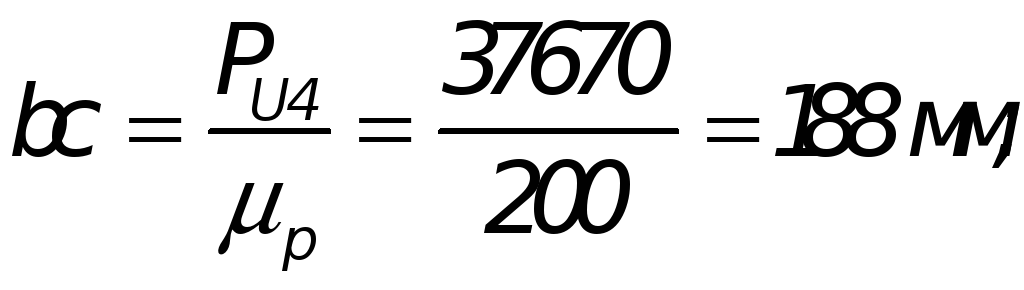
Вектор
, являясь геометрической суммой векторов
ha
, и ab,
представляет в масштабе
полную реакцию
:
Чтобы определить реакции в кинематической паре F, составляем уравнение равновесия сил, действующих на звено 4:
где
-
реакция
со стороны звена 5 на звено 4
Реакция
со стороны звена 4 на звено 5 равна по
величине реакции
и противоположна ей по направлению:
=
-
Переходим
к расчету группы 2-3, состоящей из звеньев
- 2 и 3. На группу
2-3
действуют известные по величине и
направлению силы
,
G3
,
, P'u2
=
,
=
,
,
-
реакция со стороны звена 4 на звено 3,
связанная с реакцией
зависимостью
=
-
.
Представляем
реакции
и
в виде тангенциальных и нормальных
составляющих.
Для
определения реакции
составляем уравнение моментов всех
сил, действующих на звено 2, относительно
точки С:
откуда
Для
определения реакции
составляем
уравнение моментов всех сил, действующих
на звено 3, относительно точки Н:
,
откуда
Для определения реакций в кинематических парах В и А построим план сил для двухповодковой группы 2 – 3 в целом согласно векторному уравнению
+
+
+
+
+
+
+
+
=
0
Силы
и
и
в уравнение не записываем, так как при
построении плана сил они взаимно
уравновешиваются. Масштаб плана сил
= 200 Н/мм.
Вычисляем длины векторов, изображающих известные силы, входящие в уравнение и строим план сил.
Из
плана сил определяем величины и
направления сил
и
, а также полных реакций
Чтобы
определить реакции в кинематической
паре А, составляем уравнение равновесия
сил, действующих на , звено 2 (отбросив
звено 3, а действие его на звено 2 выразив
реакцией
Согласно
плану сил реакцию
определяем
по величине и направлению вектора
:
Реакция
равна по величине реакции
и противоположна ей по направлению:
=
-
Производим
расчет ведущего звена. На кривошип АВ
действуют:
со стороны звена 2 реакция
и
со стороны стойки реакция
.
Кроме этих сил в точку В кривошипа
перпендикулярно
к оси звена приложим уравновешивающую
силу
.
Сила
полностью
известна (по величине и направлению),
а силы
и
не известны.
Вначале
определяем величину силы
.
Для этого составляем уравнение моментов
всех сил, действующих на звено 1,
относительно точки А:
-Pyp .O1 A + R21 .hR21 = 0 , откуда
Реакцию
по
величине и направлению определяем
путем построения плана сил, действующих
на звено 1, согласно векторному уравнению
Масштаб
плана сил принимаем
Из
плана
