Биполярный транзистор
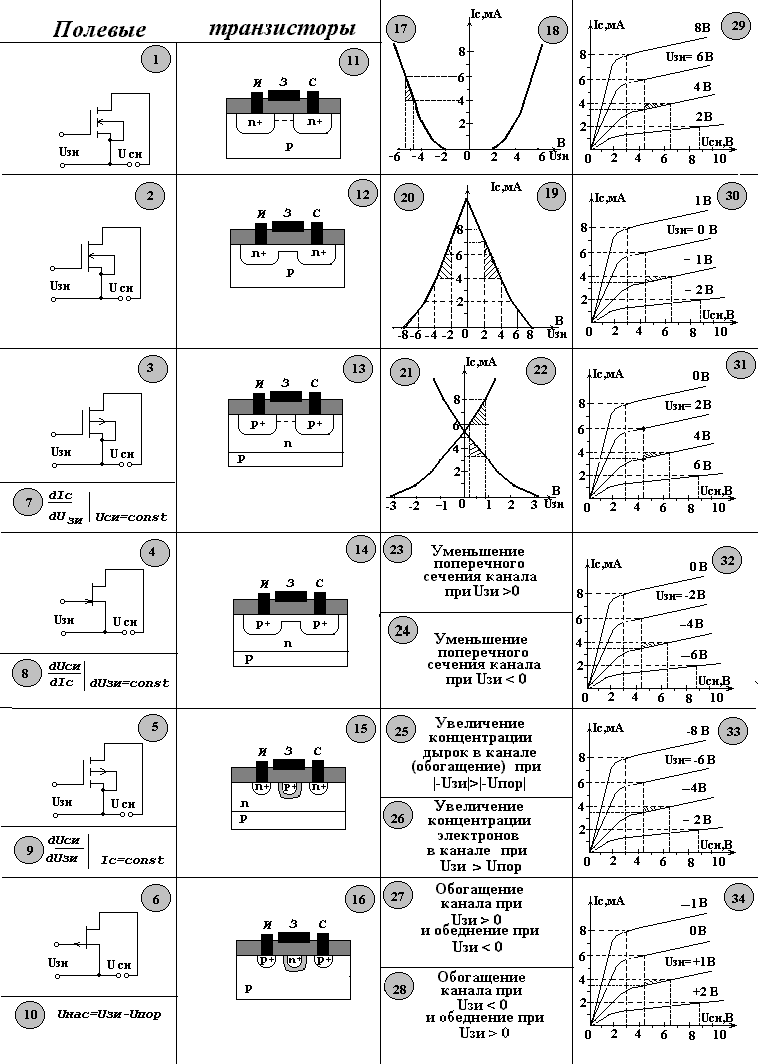
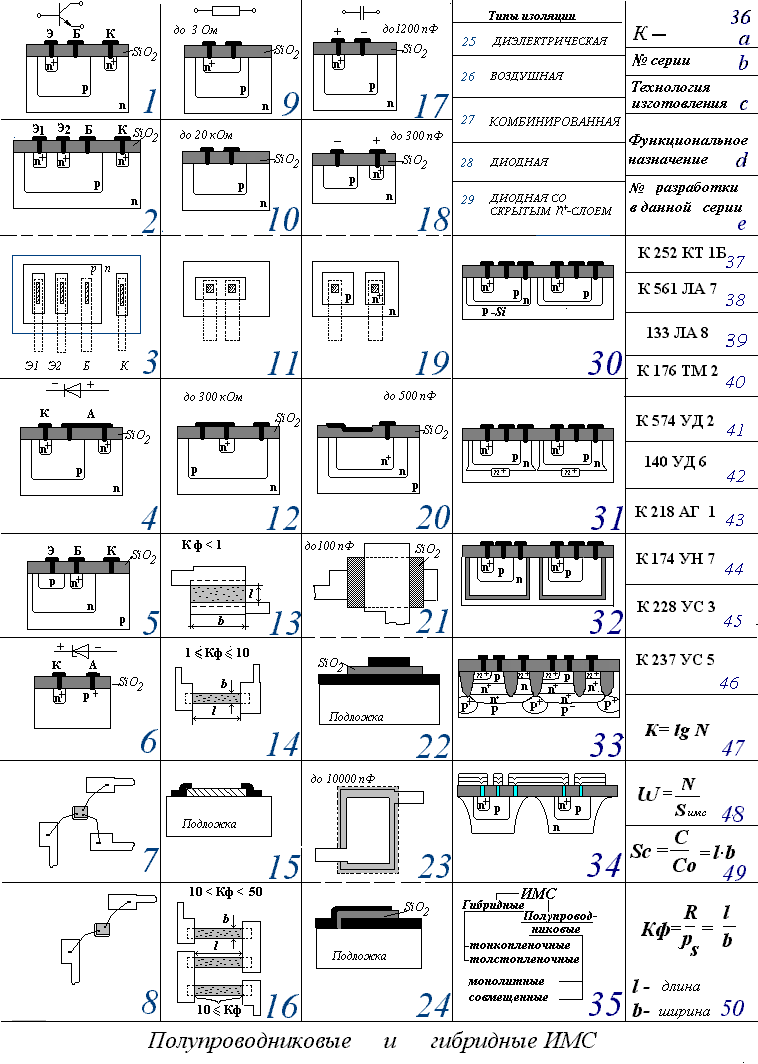
Описание к КПК «Диодное включение транзисторов»
Диоды полупроводниковых микросхем
По технологическим соображениям в качестве диодов в полупроводниковых микросхемах используют р-n-переходы транзисторных структур: эмиттерный или коллекторный, а так же их сочетание.
Пять возможных вариантов диодного включения транзисторов представлены на КПК (рис.1-5). Каждой из схем 1-5 соответствует определенный признак схемы (рис. 16-20), эквивалентная схема (рис. 11-15) и некоторые параметры: напряжение пробоя (29-30), барьерная емкость используемого перехода (21-24), время восстановления обратного тока диода - параметр, отвечающий за быстродействие – (рис. 25-28). Например, схема 5 с признаком Uкб=0 (рис.18) имеет разрез структуры – рис.6 и эквивалентную схему 12. Работает в этой схеме переход эмиттер-база, значит барьерная емкость, действующая на переходе – Сэб. Эту схему целесообразно использовать в быстродействующих цифровых микросхемах, т.к. заряд накапливается только в базе, поэтому время восстановления обратного тока (т.е. время переключения диода из открытого в закрытое состояние) минимально – 10 нс (рис. 25). В схемах, где работает эмиттерный переход, напряжение пробоя не превышает 5...8 В, барьерная емкость 0,5 пФ, а у диодов на основе коллекторного перехода напряжение пробоя 20...50 В, барьерная емкость 0,7 пФ.
Параметры схем различны, так как концентрация примесей (а значит и носителей) больше в эмиттерном переходе, и площадь коллекторного перехода больше площади эмиттерного.
Описание к КПК «Логические элементы»
Цифровыми
интегральными схемами (ЦИС) называют
микросхемы, работающие с цифровыми
сигналами. Обычно используется двоичный
код, т.е.
сигнал может принимать одно из двух
значений, условно называемых «0» и «1».
Мы будем рассматривать положительную
логику, т.е.
считать, что логическому нулю соответствует
низкий, а логической единице – высокий
уровень напряжения. Их можно определить
по передаточной характеристике, которая
показывает зависимость выходного
напряжения от входного (рис.29). Кроме
логических уровней
и
по
ней можно определить параметры 30-34:
уровни напряжения помех, способные
вызвать ложное переключение из состояния
логической единицы в состояние нуля и
наоборот, и перепад логического сигнала.
Цифровые микросхемы также характеризуются
параметрами: среднее
время задержки распространения (рис.
36), средняя
потребляемая мощность (рис.
35) и работа
переключения (рис.
37). Они
характеризуют быстродействие,
экономичность и качество микросхемы.
Логические элементы классифицируют, прежде всего, по выполняемым функциям. Различные логические выражения могут принимать одно из двух значений: «истинно» или «ложно». Для обозначения истинности или ложности используют символы 1 и 0. Все возможные логические функции любого числа логических переменных можно образовать с помощью трех операций: логического отрицания (инверсии, операции НЕ), логического сложения (дизъюнкции, операции ИЛИ) и логического умножения (конъюнкции, операции И).
Операция НЕ (инверсия) состоит в том, что входная переменная принимает на выходе инверсное значение. Суть логической операции удобно представлять в виде таблицы истинности (рис. 16), в которой X – входная величина, Y – выходная. В виде формулы операция НЕ записывается как показано на рис. 15.
Верхняя черта здесь обозначает отрицание и читается как «Y равно не X». Логический элемент НЕ имеет только один вход и один выход и обозначается так, как показано на рис. 8.
Операция И (логическое умножение, конъюнкция) - рис. 7,12,19.
Операция ИЛИ (логическое сложение, дизъюнкция) - рис. 6,11,20.
Наибольшее распространение получили элементы И–НЕ и ИЛИ–НЕ. Операции ИЛИ–НЕ и И–НЕ являются логически полными: имея набор только элементов И–НЕ либо ИЛИ–НЕ, можно выполнить любую логическую операцию.
Операция ИЛИ–НЕ – рис. 9, 13, 17
Операция И–НЕ – рис. 10, 14, 18.