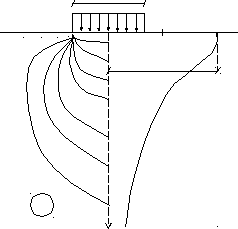
Определение напряжений в грунте

В основе задачи лежит решение о действии сосредоточенной силы, приложенной к поверхности упругого полупространства, полученное в 1885г. Ж. Буссинеском. Для определения осадок важны вертикальные напряжения , поэтому по Буссинеску:

, где

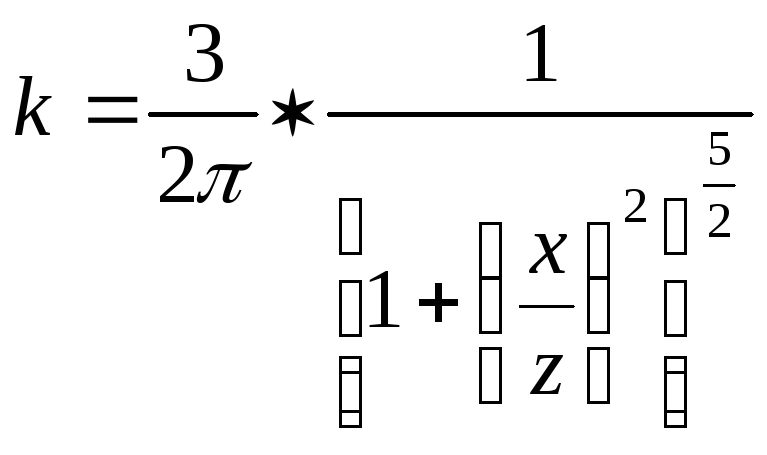
При этом, возможно, использовать принцип суперпозиции.

Если на поверхности полупространства действует распределённая нагрузка, в пределах сложного замкнутого контура, то для определения напряжений в грунте можно воспользоваться следующим приёмом:

Тогда равнодействующая сосредоточенная сила, действующая по i-му прямоугольнику , будет равна

Таким образом, получим систему сосредоточенных нагрузок , для которых можно применить принцип суперпозиции и установить действующие в грунте напряжения.

Если мы решаем плоскую задачу, т.е.

=

то для этого случая получены точные решения для определения компонент напряжений в любой точке упругого полупространства. Эти решения имеют сложные выражения. Однако их можно представить в виде:

,

где - так называемые коэффициенты влияния, которые зависят от безразмерных параметров и , где x, z – координаты точки, в которой определяются напряжения;

- ширина полосы загружения

Зная ширину фундамента “b” и задавая запись координатами точки, где требуется определить напряжения, вычисляются и , и находятся напряжения.

Иногда удобнее пользоваться главными напряжениями, т. и .

Для случая нагружения полосовой равномерно распределённой нагрузкой можно использовать формулу И. Х. Митчела (смотреть последний рисунок):

, где - угол видимости, образованный лучами, исходящими из точки к краям полосы нагрузки. При этом, действует по биссектрисе угла , а - в перпендикулярном ей направлении.

			0,9
			0,7
			0,5
			0,3
	изолинии
		0,1
			z

			b
	-2b
					x
	b	0,3
		0,2
	0,1
			z

-2b	-b			P=1	x
b
	0,2
	0,1
			z