Тема 9 Оформлення та зміст проекту нормативів гдв забруднюючих речовин у атмосферне повітря Практичне заняття 9 (№ зан. 23) – Задачі з оцінки екологічних процесів у ґрунтах

Одним із найважливіших підходів до визначення та інтегральної оцінки впливу пестицидів на здоров'я населення є вивчення динаміки їх поширення і трансформації в різних середовищах, у тому числі в ґрунтах.

Теоретичною моделлю розчинення, перенесення, поглинання й розпаду пестицидів у ґрунтах у разі одновимірного руху розчину в пористому середовищі є рівняння дифузії:

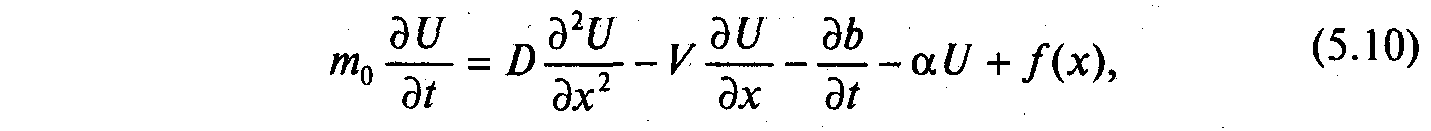
де D = D_M +X\V\ — дифузійна складова; а — коефіцієнт швидкості розпаду пестициду;

U — концентрація пестициду в розчині; V — швидкість фільтрації; db/dt — швидкість розчинення пестициду у воді; f(х) — функція поглинання пестициду кореневою системою.

Для квазістаціонарного випадку, коли V не залежить від х і m₀ = const, швидкість фільтрації розраховується з умови

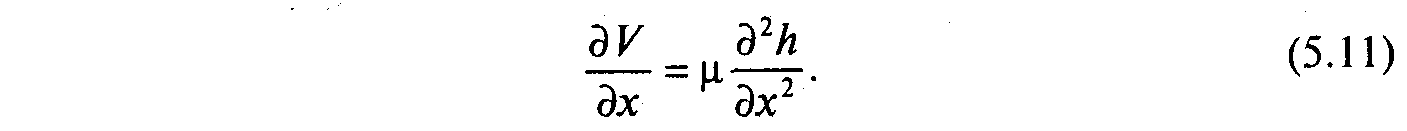Кінетику процесу розчинення і розпаду можна описати рівнян­ням першого порядку:

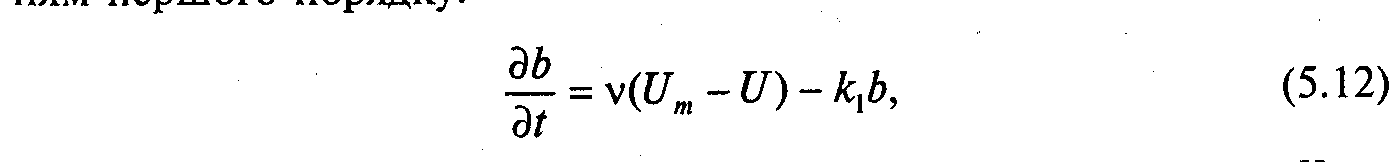де k₁ ,v — константи розпаду в твердій фазі (в сухих ґрунтах); U_m — концентрація насичення;

b — концентрація пестициду в твердій фазі ґрунтів.

Точкові моделі. На сьогодні часто обмежуються розглядом «точ­кових» моделей, хоч таке спрощення може бути вкрай небезпеч­ним: усереднюючи поведінку пестициду в просторі, тим самим не враховують можливість нагромадження його в окремих точках простору вище за норми гранично допустимих концентрацій (ГДК).

Виходячи з механізму явищ, основаного на тому, що процес роз­кладу речовини в ґрунтах здійснюється пропорціонально поточній концентрації цієї речовини, а весь комплекс факторів, що діє на зміну концентрації пестицидів і радіонуклідів у часі, виражається через усереднений коефіцієнт к, кінетику розпаду пестицидів можна описати рівнянням

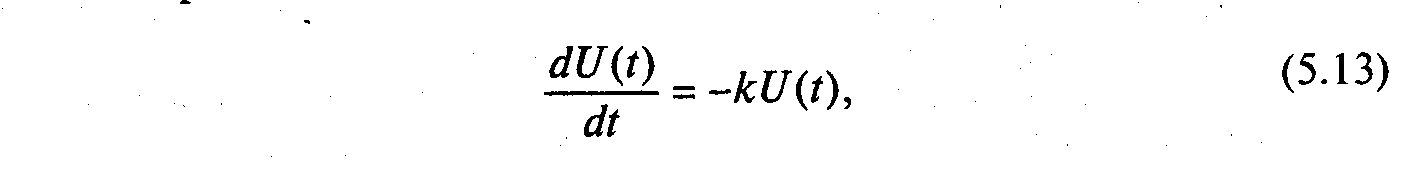розв'язок якого має вигляд

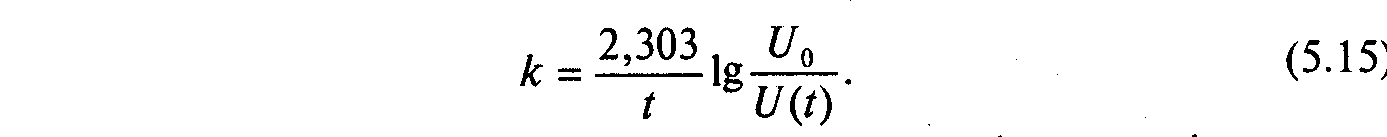де U(t) — кількість пестициду на момент часу t; U_o — початкова кон­центрація пестициду; k — константа швидкості реакції розпаду пестициду; t — час.

Основним параметром хімічної кінетики є швидкість її реакцій, що обчислюється як

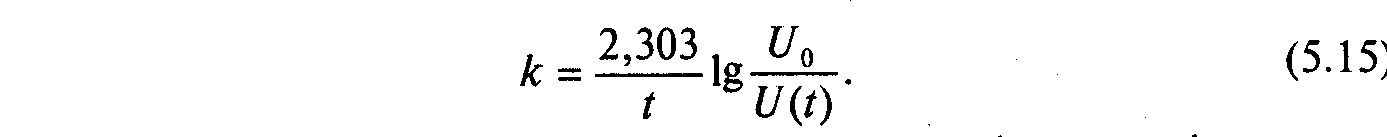U(t) Час деструкції пестициду характеризується періодом напіврозпаду.

Означення 5.1. Період напіврозпаду Т_{t /2} — це проміжок часу, протягом якого початкова концентрація речовини зменшується вдвое Знаючи k, період напіврозпаду обчислюється за формулою

Т_{1/ 2}= 0,693 /k. (5.16

Означення 5.2. Час розпаду до безпечних концентрацій — проміжок часу, протягом якого початкова концентрація речовини зменшується до рівня ГДК, тобто U(t) ==U_ГДК. З рівняння (5.14) випливає, що час розпаду пестициду

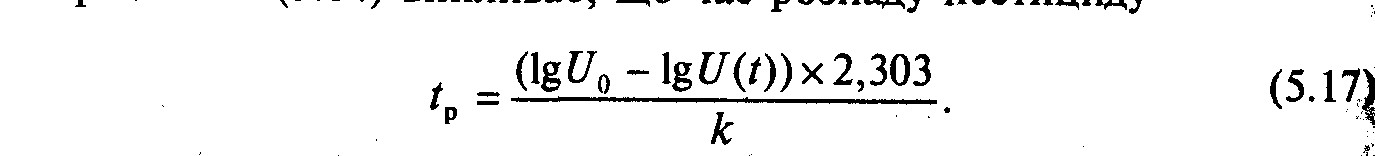
Приклад 5.3. Початкова концентрація U_o будь-якого пестициду, приклад рогору, в цукрових буряках дорівнює 12,5 мг/кг, UU) — гранично допустима концентрація рогору для цукрових буряків стансі, вить 1 мг/кг. Експериментально встановлено, що k = 0,182 доби Звідси обчислимо час розпаду до безпечних концентрацій для рогору від дня взяття проби:

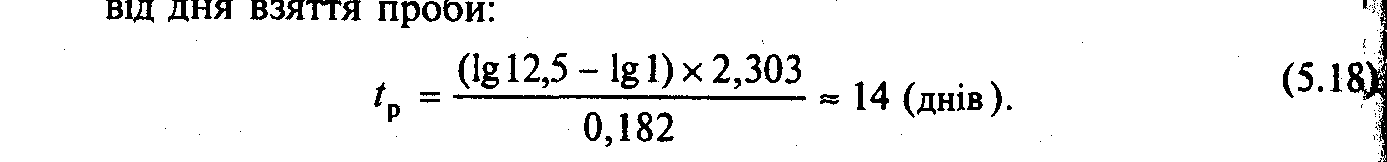За природних умов константа розпаду може залежати від різних факторів, до яких належать: фізико-хімічні властивості препарату(молекулярна маса, температура плавлення або кипіння, розчинність! у воді та жирах, стійкість при різних РН, леткість); фізико-хімічні властивості грунту (вміст гумусу, середня температура грунту, рН, вологоємкість, механічний склад, кількість фосфорних сполук, вміст азотних сполук, мікроорганізми); умови обробки ґрунту (кількість і спосіб внесення препарату, його товарна форма, кратність обробки, вид покривної культури); кліматичні умови (температура атмосферно­го повітря, його відносна вологість і швидкість вітру, кількість опадів та їх періодичність) та деякі інші фактори, що впливають на швидкість розпаду певного пестициду.

Виходячи з цього, рівняння (5.13) запишемо в різницевій формі:

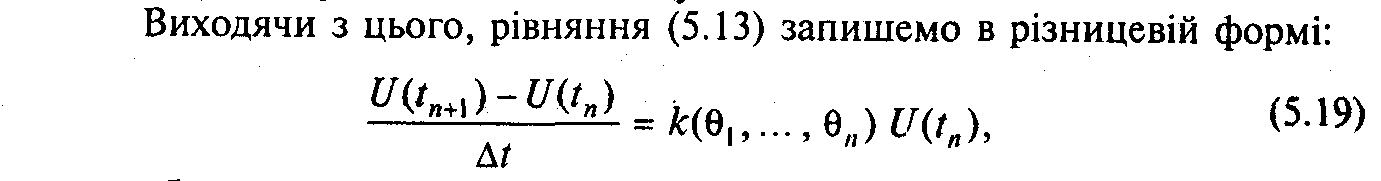
або

де a = (1- tk(е„...,е_я));

₁,..., _n — параметри природних елементів, від яких залежить кон­станта розпаду.

Різницеві рівняння (5.19) або (5.20) можуть бути використані для знаходження точніших моделей про зміну концентрації пестицидів у часі під дією різних факторів навколишнього середовища. Для цього використовують методи групового врахування аргументів.

Приклад 5.4. Прогнозована величина С(t) — концентрація далапону в ґрунті. Вхідні змінні — концентрація даної речовини в початко­вий момент C(t₀), рН ґрунту і час t з моменту внесення далапону в ґрунт. Вихідна величина та права частина вибрані як:

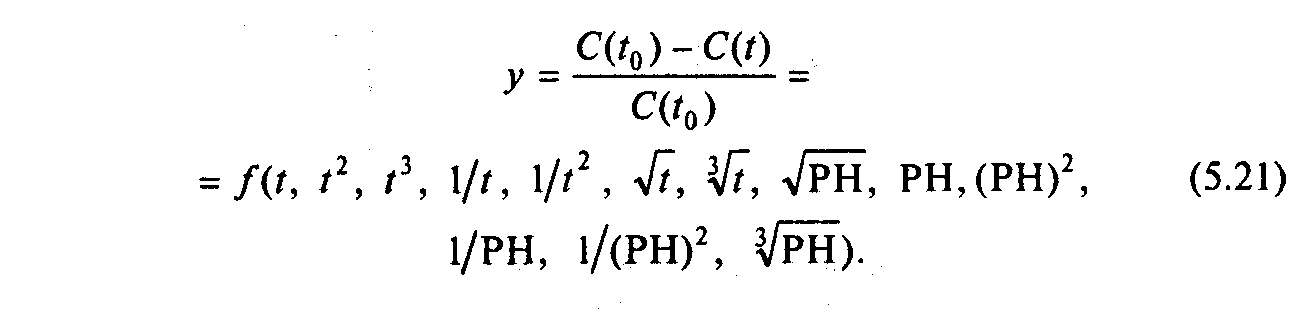У результаті обробки даних за алгоритмом МГВА знайдено такі мо­делі:

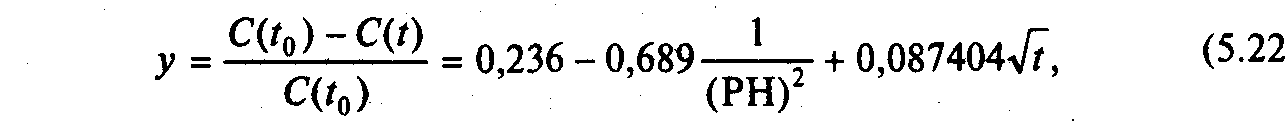а також

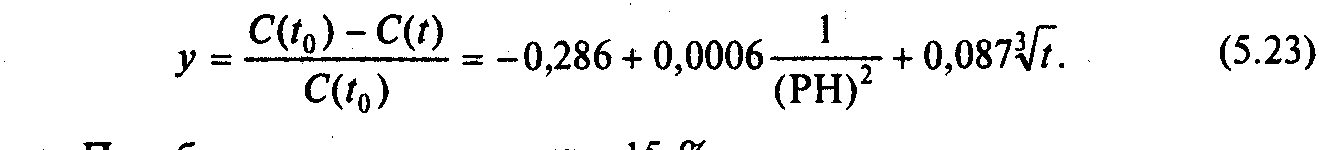Похибка прогнозу становить 15 %.

Пестициди за оцінкою експертів належать до складу небезпечні:

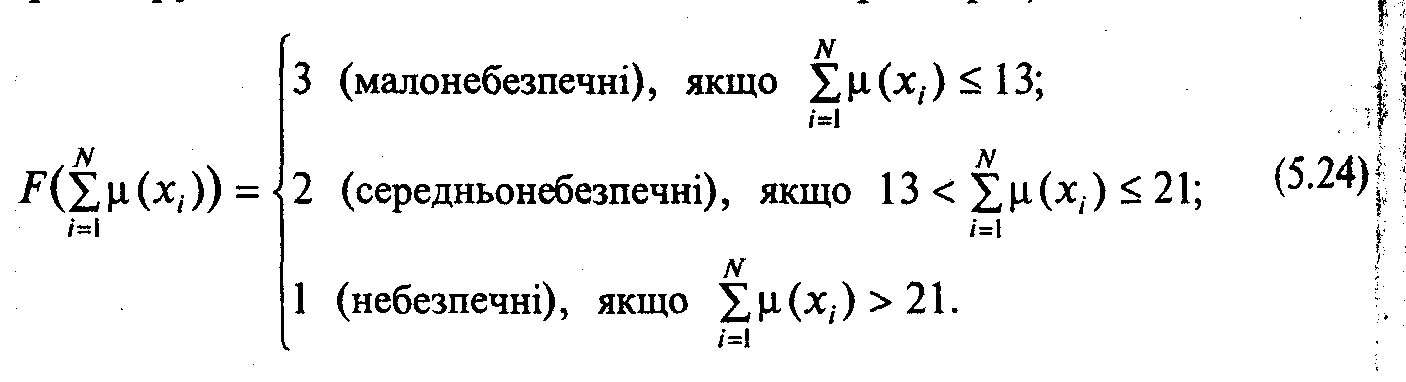
- оціночний бал

Практичне №11

Моделі міграціі у грунтах

Існує задача,що визначає f залежності від С,Т, кліматичні умови.

Так,дослідження поведінки ВМ і пестицидів показами експоненціальну залежність лінійних реакцій. Детально не можливо,тому що окремі прості реакції за сукупністю ефектів відповідно до закону діючих має .Вихідні Данні моніторингу-це сукупний ефект трансформації і транс локації у системі

“ грунт-рослини-вода-повітря”

Імперичне і хронічне забруднення неогран сполучень розглядаються на базі балансової оцінки шляхів в міграції ВМ у системі “ грунт-вода-повітря-біота” за кругообігом речовин за моделлю Енгельгарда .

ВМ: зменшення рухомих форм

r-const швидкості виведення Ме (0-20)см грунту

у глибині змінюється залежність

- рівняння Коллера

Час як итоксикологічний показник

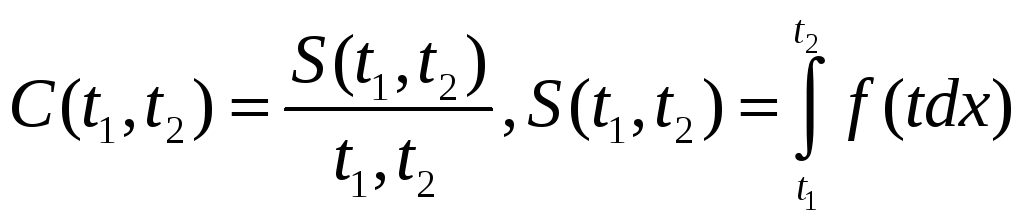
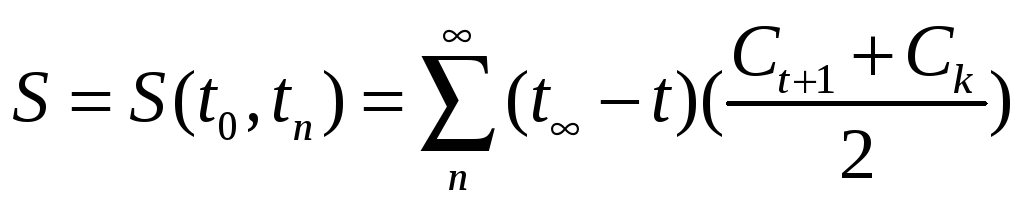
Вивчення рухомості- коєфіціент-імобілізіції-мобілізації

- рухомість при певних заходах

Практика№13

Оцінка стану природних грунтів

Методи моделювання для ідентифікації моделі

за данними натурних спостережень

Методи самоорганізації;

Сплайн-апроксимації

Ієрархічні моделі експертно-логічних систем ПР

Цей принцип передбачає пошук моделі оптимальної складності за зовнішніми критеріями :min критерію визначає модель;

За умови стохастичності зовнішньго середовища і наявності детермінованої інформичні???? Моделювання екологічних процесів на підставі сплайн-функцій,множина залежностей ,зумовлену стохастичним параметром середовища

Для аналізу стану довкілля за моніторингом і прогнозування за допомогою ієрархічної експертно-логічних моделей ПР

Загалом це

Y-вихідний вектор

-матриця вхідних даних

За експериментальними даними реалізується методи прямого моделювання

За принципом евристичної самоорганізації з розв’язанням 2 задачи:

1)визначення структури структури оператора при виконанні алгоритма метода групового врахування аргументів МГВА

2)оцінки параметрів оператора

За МГВА силою масової селекції повний опис об’єкта

Де -невідома функція з кількома рядами “частинних” описів

Як оцінюють за критеріями селекції на другий ряд,де -вхідні змінні

…………………………………………………………..

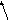
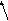
Структура алгоритму самоорганізації у вигляді відображення,

Частинний опис: яке переводить на кожному r-му кроці множину

в (вектор r-ряда)

Багатомірний процес – S мережа з дугами

З вершинами поліноміальних алгоритмів МГВА визначається за МНК

Тренди тільки на 1-ому кроці, далі прописується залишок:

Р_j оператори ортогонального проектування поєднуються:

- суперпозиція операторів

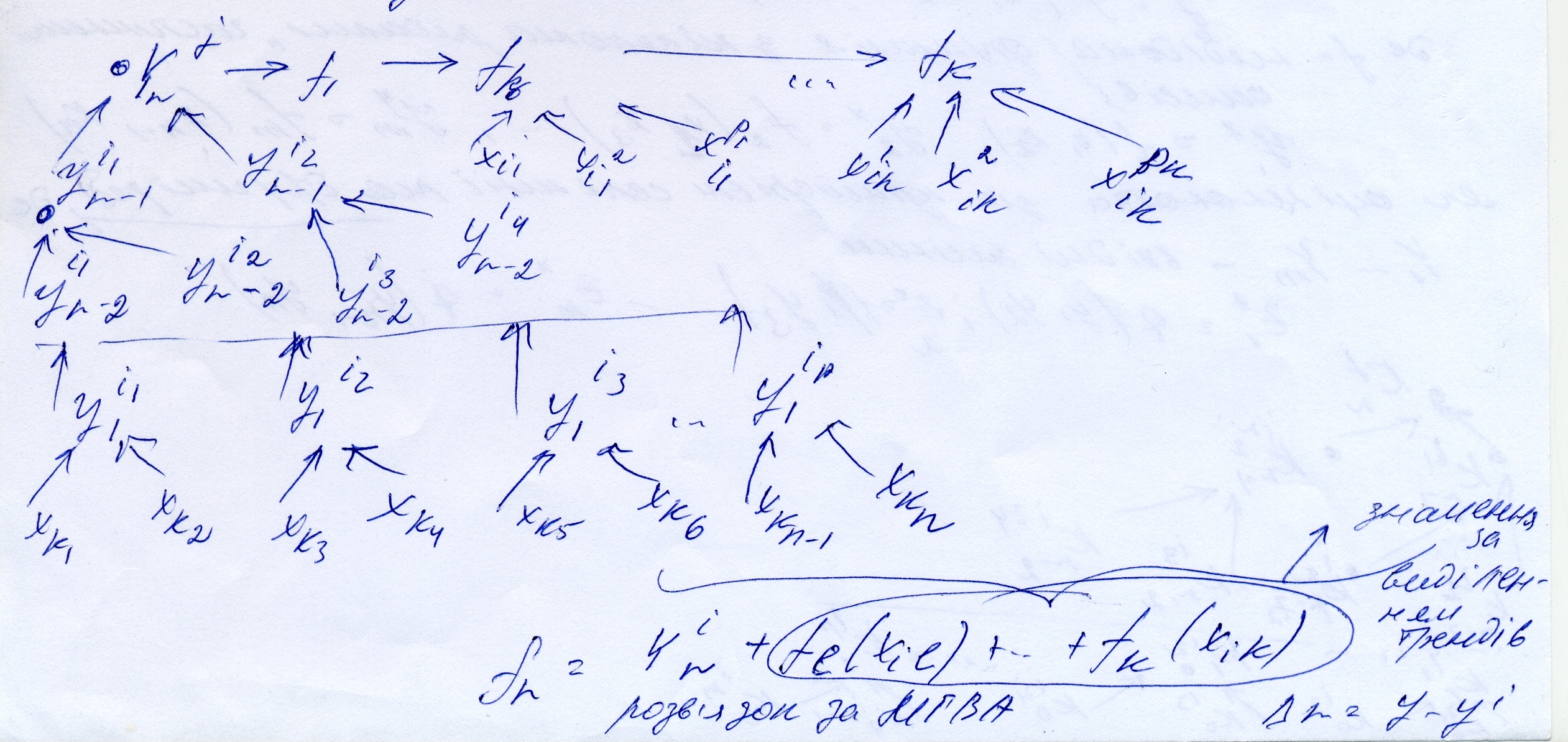
значення за виділенням трендів

Розв’язок за МГВА