6Б. Варианты задач для групп по специальности ″математические методы в экономике″
ТЕМА ″ТРАНСПОРТНЫЕ СЕТИ″
Транспортная
сеть
задана списком дуг
,
где
– начало дуги,
– конец дуги, а
– пропускная способность дуги.
-
Построить все
-разрезы
сети; -
Используя помечающий алгоритм, построить максимальный поток
сети и вычислить его значение.
|
ГРУППА ЭКОНОМ. КИБЕРНЕТИКА 2 КУРС 2011∕ 2012 УЧ. ГОД |
||
|
ВАРИАНТ |
ФИО |
Оценка |
|
1 |
Ахметзянова Лилия |
|
|
2 |
Билалова Лейла |
|
|
3 |
Вафина Альфинур |
|
|
4 |
Гараева Гульшат |
|
|
5 |
Глебова Валерия |
|
|
6 |
Зюмрва Елена |
|
|
7 |
Крылов Сергей |
|
|
8 |
Райхлина Екатерина |
|
|
9 |
Савельева Маргарита |
|
|
10 |
Салихова Айназ |
|
|
11 |
Титоренко Роман |
|
|
12 |
Тубольцева Ксения |
|
|
13 |
Фейсханов Алмаз |
|
|
14 |
Цуканова Ольга |
|
|
15 |
Чудаева Алина |
|
|
16 |
Шайдулова Софья |
|
|
17 |
Яковлева Екатерина |
|
7.Задачи по теме ″рекурсивные функции″.
1. Доказать, что следующие функции примитивно рекурсивны:
1)
(где
−
константа)
2)
3)
(где
)
4)
5)
6)
(где
)
7)
8)
9)
10)
11)
,
;
12)
|
;
13)
14)
15)
−
функции
алгебры логики (отрицание, дизъюнкция,
конъюнкция),
где чётные числа трактуются как
,
а нечётные
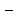как
,
т.е.
16)
− произвольная
функция алгебры логики;
17)
где
примитивно рекурсивная функция,
;
18)
где
примитивно рекурсивная функция,
;
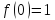19)
(здесь
);
20)
rest
(
,
)
(здесь
rest(
,
)
);
21)
(при фиксированном
);
22)
(при фиксированном
,
);
23)
(
,
)
наибольший общий делитель чисел
и
(здесь (
,
)
= 0);
24)
[
,
]
наименьшее общее кратное чисел
и
(здесь
[
,
= [
,
]
0);
25)
−
число сочетаний из
по
(здесь
0
при
);
26)
27)
где
,
,
,
примитивно
рекурсивные функции от переменных
.
2.
Применяя операцию примитивной рекурсии
к функциям
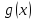и
,
определить функцию
и записать её в аналитической форме:
1)
,
;
2)
,
;
3)
,
;
4)
,
;
5)
,
;
6)
,
;
7)
,
;
8)
,
9)
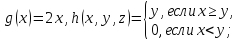
10)
3. Вычислить соответствующую функцию, применяя операцию минимизации. Результаты представить в аналитической форме:
1)
[|
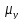−3| = 0];
2)
[|
−
| = 0];
3)
[|
−
| = 0];
4)
[
−
= 0];
5)
[|
−
|= 0];
6)
[|
−
| = 0];
7)
[|
−
| = 0];
8)
[|
−
| = 0];
9)
[|
−
| = 0];
10)
[|
−
| = 0];
11)
[|
−
| = 0];
12)
[|
−
| = 0];
13)
[|
−
| = 0];
14)
[|
−
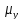| = 0].
4. Доказать, что следующие функции частично рекурсивны:
1)
нигде не определённая функция;
2)
3)
4)
6)
функция, определённая только при
,
,…,
.
5.
Найти примитивно рекурсивную функцию,
из которой однократным применением
операции минимизации можно получить
частично рекурсивную функцию
:
1)
;
2)
;
3)
;
4)
5)
;
6)
;
7)
;
8)
;
9)
.