
- •Задачи для программирования по темам
- •Направление ″бизнес-информатика″, специальность ″математические методы в экономике″
- •1 . Обходы графа . Вычисление числа компонент связности графа.
- •2. Алгоритмы поиска путей в графе.
- •3. Алгоритмы нахождения минимального остова в графе
- •4. Хроматическое число графа. Алгоритм правильной раскраски вершин графа методом перебора с возвратами.
- •5. Транспортные сети. Теорема форда-фалкерсона о максимальном потоке в транспортной сети
- •6А. Варианты задач для групп по направлению ″бизнес-информатика″ тема ″транспортные сети″
- •6Б. Варианты задач для групп по специальности ″математические методы в экономике″
- •7.Задачи по теме ″рекурсивные функции″.
- •1. Доказать, что следующие функции примитивно рекурсивны:
- •8. Задачи по теме ″машины тьюринга″
- •2. (Гаврилов г. П., Сапоженко а.А. Задачник. С. 220-221, идея из № 1.2.) Построить машину в алфавите , , которая:
- •3. (Гаврилов г. П., Сапоженко а.А. Задачник. С. 221, № 1.3.) По заданной машине Тьюринга и начальной конфигурации найти заключительную конфигурацию:
- •4. (Лавров и.А., Максимова л.Л. С. 138, № 1.) Какую функцию вычисляет машина Тьюринга со следующей программой п:
- •5. (Лавров и.А., Максимова л.Л. С. 139, № 5.) Построить следующие машины Тьюринга в алфавите , , начальную конфигурацию в заключительную конфигурацию :
2. Алгоритмы поиска путей в графе.
Постановка
задачи.
Дан простой ориентированный граф
 с множеством вершин
с множеством вершин
 и множеством рёбер
и множеством рёбер

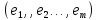 (без петель и кратных дуг). На множестве
дуг задана неотрицательная
вещественная функция
(без петель и кратных дуг). На множестве
дуг задана неотрицательная
вещественная функция
 (длины дуг). Длина
пути
из вершины
(длины дуг). Длина
пути
из вершины
 в вершину
в вершину
 определяется
как сумма длин дуг, составляющих путь
.
определяется
как сумма длин дуг, составляющих путь
.
Задача 1. Одна из вершин выделена как источник. Требуется найти кратчайшие пути из источника ко всем остальным вершинам.
Задача 2. Найти кратчайшие пути между всеми парами вершин.
Для решения задачи 1 рассмотрим ″жадный″ алгоритм Дейкстры:
Алгоритм
строит (использует) множество
 вершин, для которых кратчайшие
пути из источника уже найдены. На каждом
шаге к множеству
вершин, для которых кратчайшие
пути из источника уже найдены. На каждом
шаге к множеству
 добавляется та из оставшихся вершин
добавляется та из оставшихся вершин
 которая ближе к источнику по сравнению
с другими оствшимися вершинами. Так
как длины дуг неотрицательны, то можно
быть уверенны в том, что кратчайший путь
проходит от источника к конкретной
вершине через вершины множества
которая ближе к источнику по сравнению
с другими оствшимися вершинами. Так
как длины дуг неотрицательны, то можно
быть уверенны в том, что кратчайший путь
проходит от источника к конкретной
вершине через вершины множества
 .
На каждом шаге алгоритма используется
массив
.
На каждом шаге алгоритма используется
массив
 ,
в который записываются длины кратчайших
путей для каждой вершины. Причём если
,
в который записываются длины кратчайших
путей для каждой вершины. Причём если
 ,
то значение
,
то значение
 становится окончательным.
становится окончательным.
Алгоритм Дейкстры
Пусть dist – двумерный массив, причём dist [v,w] равно длине дуги (v,w) из вершины v в вершину w. Если такой дуги не существует, то полагаем dist [v,w]= ∞.
S
← {1}; вершина
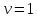 взята как источник
взята как источник
L[1] ← 0;
for v ← 2 to n do
L[v] ← dist [1,v]; pred[v] ← v
od;
for i ← 1 to n − 1 do
найдём вершину w ∈ V \ S, для которой значение L[w]минимально;
S ← S ∪ {w};
for ∀v ∈ V \ S do
m ← L[w] + dist [w,v];
if L[v] > m then {L[w]← m; pred[v] ← w
od
od.
Результат: L[v]− длина кратчайшего пути из вершины 1 в вершину v. При этом v, pred[v], pred[pred[v]],..., 1 есть вершины, составляющие кратчайший путь из вершины 1 в вершину v.
Обоснование алгоритма Дейкстры (кратко)
Допустим,
что для полученного пути из источника
 в
в
 имеется более короткий путь в
имеется более короткий путь в
 ,
который проходит до вершины
,
который проходит до вершины
 через вершины множества
через вершины множества
 и выходит из него, затем путь, возможно,
несколько раз заходит в
и выходит из него, затем путь, возможно,
несколько раз заходит в
 и выходит из него, пока не достигнет
вершины
и выходит из него, пока не достигнет
вершины
 .
В этом случае вместо
.
В этом случае вместо
 была бы выбрана вершина
была бы выбрана вершина
 .
Противоречие.
.
Противоречие.
Другая
возможность кратчайшего пути не
реализуема, поскольку путь из
 в
в
 через вершины множества
через вершины множества
 короче, чем через вершину
короче, чем через вершину
 по построению.
по построению.
Рассмотренный
алгоритм имеет временн ю
сложность O
(
ю
сложность O
( ).
Для рещения второй задачи существует
алгоритм (Флойда , основанный на процедуре
Уорщолла для вычисления транзитивного
замыкания) со сложность
O
(
).
Для рещения второй задачи существует
алгоритм (Флойда , основанный на процедуре
Уорщолла для вычисления транзитивного
замыкания) со сложность
O
( ),
причем допускаются даже отрицательные
веса дуг графа.
),
причем допускаются даже отрицательные
веса дуг графа.
3. Алгоритмы нахождения минимального остова в графе
Постановка
задачи.
Дан
простой неориентированный граф
 с множеством вершин
с множеством вершин
 и множеством рёбер
и множеством рёбер

 (без петель и кратных дуг). На множестве
рёбер задана вещественная функция
(без петель и кратных дуг). На множестве
рёбер задана вещественная функция
 (величина
(величина
 называется стоимостью
ребра
называется стоимостью
ребра
 ).
Остов
графа
).
Остов
графа
 −любой
подграф
−любой
подграф
 ,
,
 ,
графа
,
графа
 ,
являющий деревом. Стоимость остова
определяется как сумма стоимостей
входящих в него рёбер.
,
являющий деревом. Стоимость остова
определяется как сумма стоимостей
входящих в него рёбер.
Требуется
найти остов
 графа
графа
 ,
имеющий наименьшую стоимость по сравнению
с другими возможными остовами.
,
имеющий наименьшую стоимость по сравнению
с другими возможными остовами.
Существует несколько алгоритмов решения этой задачи. Наиболее известны:
″Жадный″
алгоритм Крускала,
ориентированный на работу с рёбрами.
Его временн я
сложность равна O(
я
сложность равна O(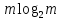 ),
где
),
где
 − число рёбер графа.
− число рёбер графа.
Алгоритм
ближайшего соседа Прима и Дейкстры,
ориентированный на работу с вершин ми.Его
временная сложность равна O(
ми.Его
временная сложность равна O( ),
где
),
где
 − число вершин графа.
− число вершин графа.
Алгоритм Крускала
1.
(Предварительная
сортировка рёбер.)
Рёбра
графа
 помещаются в очередь Q
по неубыванию их стоимостей.
помещаются в очередь Q
по неубыванию их стоимостей.
2. (Непосредственное построение остова.)
T
← ∅; искомое
множество рёбер
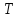 пока
не построено
пока
не построено
e ⟸ Q; извлекаем ребро из очереди
T
← T
∪
{e};
и
помещаем его в искомое множество

while
 do
множество
do
множество
 должно
содержать
должно
содержать
 рёбер
рёбер
e ⟸ Q; извлекаем очередное ребро из очереди
if ребро e не образует цикла с вершинами ранее включёнными в T
then T ← T ∪ {e}
od.
Обоснование (корректность) алгоритма
Пусть

 − рёбра построенного остова
− рёбра построенного остова
 ,
записанные в порядке неубывания их
стоимостей,
,
записанные в порядке неубывания их
стоимостей,
 – минимальный по стоимости остов графа
графа
– минимальный по стоимости остов графа
графа
 ,
которыё содержит рёбра
,
которыё содержит рёбра
 из
из
 для наибольшего возможного
для наибольшего возможного
 .
Добавление
.
Добавление
 в
в
 приводит к образованию цикла в остове
приводит к образованию цикла в остове
 ,
который будет содержать ребро
,
который будет содержать ребро
 ,
,
 .
Заметим, что
.
Заметим, что
 ,
так как в противном случае ребро
,
так как в противном случае ребро
 было бы включено в
было бы включено в
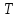 .
Допущение
.
Допущение
 также приводит к противоречию: стоимость
остова
также приводит к противоречию: стоимость
остова
 ,
где
,
где
 ,
будет меньше стоимости минимального
остова
,
будет меньше стоимости минимального
остова
 .
Значит,
.
Значит,
 .
Однако, это противоречит способу выбора
индекса
.
Однако, это противоречит способу выбора
индекса
 .
Следовательно,
.
Следовательно,
 −
минимальный остов.
−
минимальный остов.
Реализация алгоритма. Наиболее сложным в этом алгоритме является реализация оператора if Его эффективная реализация может быть осуществлена с помощью операций НАЙТИ и ОБЪЕДИНИТЬ для совокупности непересекающихся множеств.
Первоначально
искомое дерево не имеет рёбер, т.е.
 ∅, и состоит из изолированных вершин
множества
∅, и состоит из изолированных вершин
множества
 .
По мере включения в
.
По мере включения в
 рёбер образуются частичные остовы
(поддеревья), которые последовательно
объединяются в единое дерево. Ребро
рёбер образуются частичные остовы
(поддеревья), которые последовательно
объединяются в единое дерево. Ребро
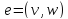 включается в
включается в
 ,
если его концы принадлежат разным
частичным остовам
,
если его концы принадлежат разным
частичным остовам
 и
и
 .
При этом остовы
.
При этом остовы
 и
и
 объединяются в один остов
объединяются в один остов
 .
Каждый такой остов представлен множеством
своих вершин, в качестве имени которого
выбирается одна из его вершин.
.
Каждый такой остов представлен множеством
своих вершин, в качестве имени которого
выбирается одна из его вершин.
(ПРИВОДИТСЯ РЕАЛИЗАЦИЯ − ПРОПУЩЕНО)
Временная
сложность алгоритма Крускала.
Временн я
сложность алгоритма равна
я
сложность алгоритма равна
O( ),
поскольку за такое время может быть
реализована как первая, так и вторая
фазы алгоритма. Алгоритм
Прима-Дейкстры
может быть реализован со сложностью O
(
),
поскольку за такое время может быть
реализована как первая, так и вторая
фазы алгоритма. Алгоритм
Прима-Дейкстры
может быть реализован со сложностью O
( ).
).
