
Індивідуальні завдання
ЗАВДАННЯ 4.1.
4.1.1.
Математичне сподівання і дисперсія
випадкової величини
![]() дорівнюють відповідно 2 і10. Знайти
математичне сподівання і дисперсію
величини
дорівнюють відповідно 2 і10. Знайти
математичне сподівання і дисперсію
величини
![]() .
.
4.1.2.
Дискретна випадкова величина
![]() має ряд розподілу
має ряд розподілу
|
X |
1 |
3 |
5 |
|
P |
0,4 |
0,1 |
0,5 |
Побудувати
ряд розподілу випадкової величини
![]() .
.
4.1.3.
Дискретна
випадкова величина
![]() має ряд розподілу
має ряд розподілу
-
X
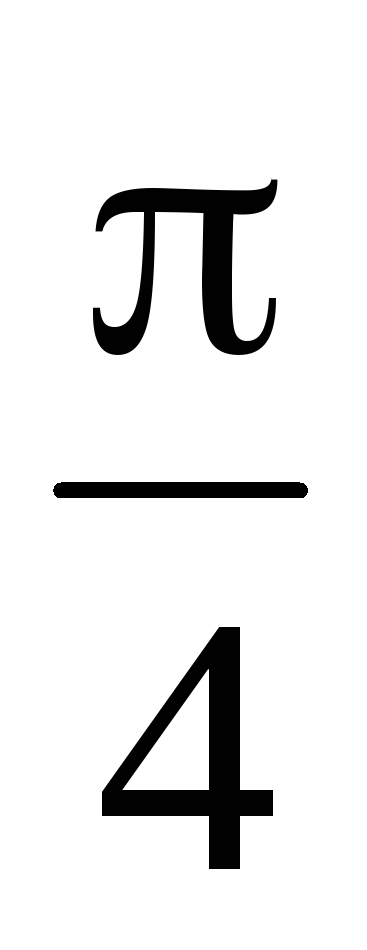
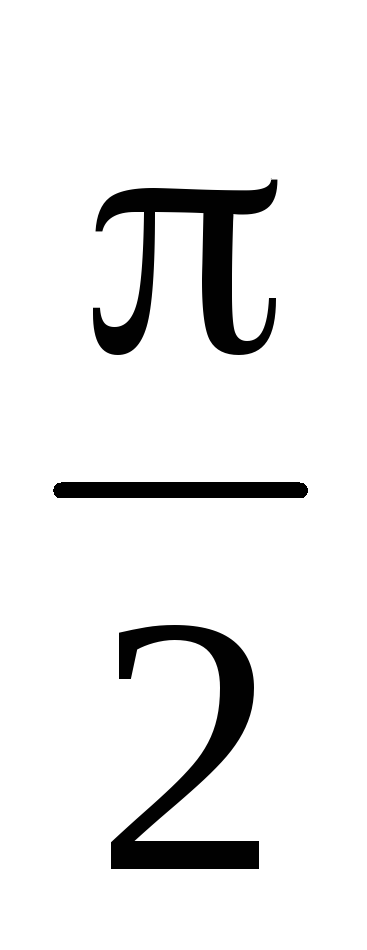
 5
5P
0,4
0,1
0,5
Побудувати
ряд розподілу випадкової величини
![]() .
.
4.1.4.
Дискретна
випадкова величина
![]() має ряд розподілу
має ряд розподілу
-
X
-2
-1
0
1
2
P
0,1
0,2
0,3
0,3
0,1
Побудувати
ряд розподілу випадкової величини
![]() .
.
4.1.5.
В умовах попередньої задачі
побудувати
ряд розподілу випадкової величини
![]() .
.
4.1.6.
Випадкова величина
![]() розподілена за нормальним законом зі
щільністю ймовірностей
розподілена за нормальним законом зі
щільністю ймовірностей
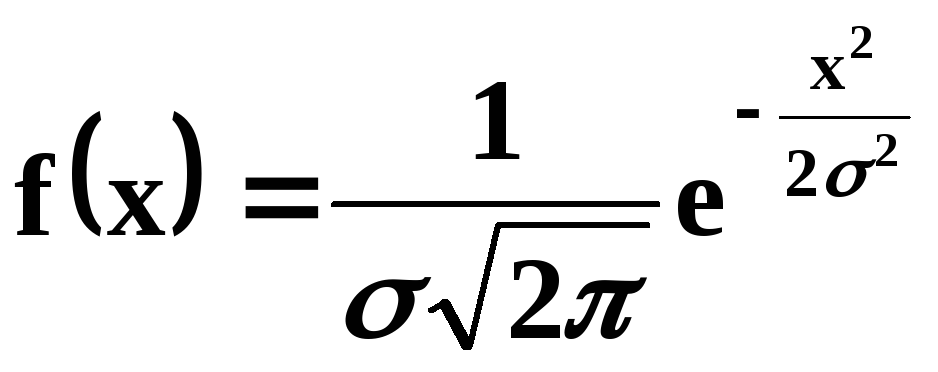 .
.
Знайти
закон розподілу випадкової величини
![]() .
.
4.1.7.
Випадкова величина
![]() має показниковий розподіл зі щільністю
ймовірностей
має показниковий розподіл зі щільністю
ймовірностей
![]() ,
,![]() .
Знайти функцію розподілу і щільність
ймовірностей випадкової величини
.
Знайти функцію розподілу і щільність
ймовірностей випадкової величини
![]() .
.
4.1.8.
Випадкова величина
![]() розподілена рівномірно в інтервалі
розподілена рівномірно в інтервалі
![]() .
Знайти закон розподілу випадкової
величини
.
Знайти закон розподілу випадкової
величини
![]() .
.
4.1.9.
Випадкова величина
![]() розподілена рівномірно в інтервалі
розподілена рівномірно в інтервалі
![]() .
Знайти закон розподілу випадкової
величини
.
Знайти закон розподілу випадкової
величини
![]() .
.
4.1.10.
Задана щільність розподілу випадкової
величини
![]() :
:
![]() в інтервалі
в інтервалі
![]() ;
за межами цього інтервалу
;
за межами цього інтервалу
![]() .
Знайти щільність розподілу випадкової
величини
.
Знайти щільність розподілу випадкової
величини
![]() .
.
4.1.11.
Випадкова величина
![]() розподілена за нормальним законом зі
щільністю ймовірностей
розподілена за нормальним законом зі
щільністю ймовірностей
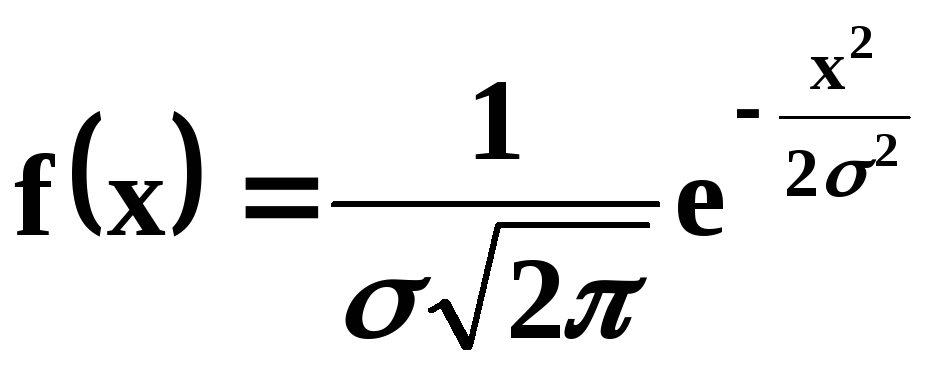
Знайти
закон розподілу випадкової величини
![]() .
.
4.1.12.
Випадкова величина
![]() розподілена за нормальним законом зі
щільністю ймовірностей
розподілена за нормальним законом зі
щільністю ймовірностей
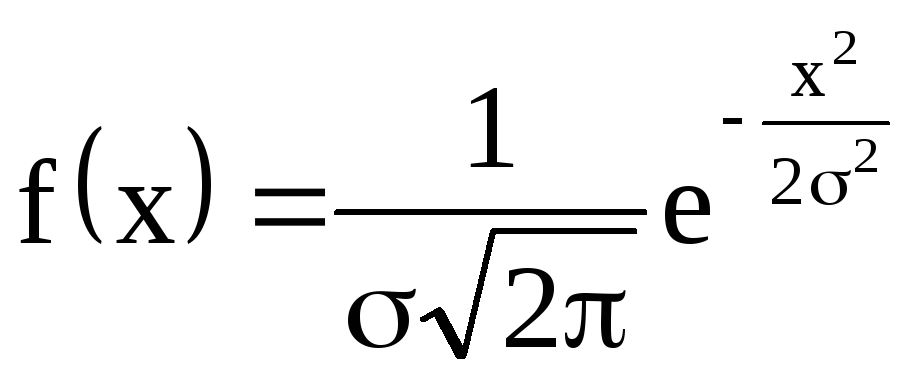 .
.
Знайти
закон розподілу випадкової величини
![]() .
.
4.1.13.
Випадкова величина
![]() задана щільністю ймовірностей
задана щільністю ймовірностей
![]() в інтервалі
в інтервалі
![]() ;
за межами цього інтервалу
;
за межами цього інтервалу
![]() .
Знайти математичне сподівання випадкової
величини
.
Знайти математичне сподівання випадкової
величини
![]() .
.
4.1.14.
Випадкова величина
![]() задана щільністю ймовірностей
задана щільністю ймовірностей
![]() в інтервалі
в інтервалі
![]() ;
за межами цього інтервалу
;
за межами цього інтервалу
![]() .
Знайти математичне сподівання випадкової
величини
.
Знайти математичне сподівання випадкової
величини
![]() .
.
4.1.15.
Випадкова величина
![]() задана щільністю ймовірностей
задана щільністю ймовірностей
![]() в інтервалі
в інтервалі
![]() ;
за межами цього інтервалу
;
за межами цього інтервалу
![]() .
Знайти дисперсію випадкової величини
.
Знайти дисперсію випадкової величини
![]() .
.
4.1.16.
Випадкова величина
![]() задана щільністю ймовірностей
задана щільністю ймовірностей
![]() в інтервалі
в інтервалі
![]() ;
за межами цього інтервалу
;
за межами цього інтервалу
![]() .
Знайти дисперсію випадкової величини
.
Знайти дисперсію випадкової величини
![]() .
.
4.1.17.
Задана щільність розподілу
![]() випадкової величини
випадкової величини
![]() ,
можливі значення якої знаходяться в
інтервалі
,
можливі значення якої знаходяться в
інтервалі
![]() .
Знайти щільність розподілу випадкової
величини
.
Знайти щільність розподілу випадкової
величини
![]() .
.
4.1.18.
Задана щільність розподілу
![]() випадкової величини
випадкової величини
![]() ,
можливі значення якої знаходяться в
інтервалі
,
можливі значення якої знаходяться в
інтервалі
![]() .
Знайти щільність розподілу випадкової
величини
.
Знайти щільність розподілу випадкової
величини
![]() .
.
4.1.19.
Задана щільність розподілу
![]() випадкової величини
випадкової величини
![]() ,
можливі значення якої знаходяться в
інтервалі
,
можливі значення якої знаходяться в
інтервалі
![]() .
Знайти щільність розподілу випадкової
величини
.
Знайти щільність розподілу випадкової
величини
![]() .
.
4.1.19.
Задана щільність розподілу
![]() випадкової величини
випадкової величини
![]() ,
можливі значення якої знаходяться в
інтервалі
,
можливі значення якої знаходяться в
інтервалі
![]() .
Знайти щільність розподілу випадкової
величини
.
Знайти щільність розподілу випадкової
величини
![]() .
.
4.1.20.
Задана щільність розподілу
![]() випадкової величини
випадкової величини
![]() ,
можливі значення якої знаходяться в
інтервалі
,
можливі значення якої знаходяться в
інтервалі
![]() .
Знайти щільність розподілу випадкової
величини
.
Знайти щільність розподілу випадкової
величини
![]() .
.
ЗАВДАННЯ 4.2.
4.2.1. Дискретні випадкові величини задані розподілами:
|
X |
0 |
2 |
4 |
|
Y |
1 |
3 |
5 |
|
P |
0,2 |
0,3 |
0,5 |
|
P |
0,5 |
0,2 |
0,3 |
Знайти
закон розподілу випадкової величини
![]() .
.
4.2.2.
В умовах попередньої задачі знайти
математичне сподівання випадкової
величини
![]() .
.
4.2.3.
Випадкові величини
![]() і
і
![]() - незалежні. Знайти дисперсію випадкової
величини
- незалежні. Знайти дисперсію випадкової
величини
![]() ,
якщо відомо, що
,
якщо відомо, що
![]() ,
,
![]() .
.
4.2.4.
Незалежні випадкові величини
![]() і
і
![]() розподілені нормально,
розподілені нормально,
![]() ,
,
![]()
![]() ,
,
![]() .
Записати щільність ймовірності і функцію
розподілу їх суми.
.
Записати щільність ймовірності і функцію
розподілу їх суми.
4.2.5.
Випадкові величини
![]() і
і
![]() незалежні і розподілені за законом
Пуассона:
незалежні і розподілені за законом
Пуассона:
![]() ;
;
![]() .
.
Знайти закон розподілу їх суми.
4.2.6.
Випадкові величини
![]() і
і
![]() незалежні і мають однаковий показниковий
розподіл із щільністю
незалежні і мають однаковий показниковий
розподіл із щільністю
![]() ;
;
![]() .
Знайти щільність
ймовірності їх суми.
.
Знайти щільність
ймовірності їх суми.
4.2.7.
Випадкові величини
![]() і
і
![]() незалежні і мають рівномірний розподіл
на відрізку
незалежні і мають рівномірний розподіл
на відрізку
![]() :
:
![]() ,
при
,
при
![]() ;
;
![]() ,
,
![]() .
Знайти функцію розподілу і щільність
ймовірностей випадкової величини
.
Знайти функцію розподілу і щільність
ймовірностей випадкової величини
![]() .
.
4.2.8. Дискретні випадкові величини задані розподілами:
|
X |
10 |
12 |
16 |
|
Y |
1 |
2 |
|
P |
0,4 |
0,1 |
0,5 |
|
P |
0,2 |
0,8 |
Знайти
закон розподілу випадкової величини
![]() .
.
4.2.9. Дискретні випадкові величини задані розподілами:
|
X |
4 |
10 |
|
Y |
1 |
7 |
|
P |
0,7 |
0,3 |
|
P |
0,8 |
0,2 |
Знайти
закон розподілу випадкової величини
![]() .
.
4.2.10.
Незалежні випадкові величини
![]() і
і
![]() задані щільностями розподілів:
задані щільностями розподілів:
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
.
Знайти
щільність розподілу випадкової величини
![]() .
.
4.2.11.
Незалежні нормально розподілені
випадкові величини
![]() і
і
![]() задані щільностями розподілів:
задані щільностями розподілів:
![]() ,
,
![]() .
.
Знайти
щільність розподілу випадкової величини
![]() .
.
4.2.12.
Задані щільності розподілів незалежних
рівномірно розподілених випадкових
величин
![]() і
і
![]() :
:
![]() ,
при
,
при
![]() ;
;
![]() ,
,
![]() .
Знайти функцію розподілу і щільність
ймовірностей випадкової величини
.
Знайти функцію розподілу і щільність
ймовірностей випадкової величини![]() .
.
4.2.13.
Задані щільності розподілів незалежних
рівномірно розподілених випадкових
величин
![]() і
і
![]() :
:
![]() ,
при
,
при
![]() ;
;
![]() ,
,
![]() .
Знайти функцію розподілу і щільність
ймовірностей випадкової величини
.
Знайти функцію розподілу і щільність
ймовірностей випадкової величини![]() .
.
4.2.14.
У прямокутник з вершинами
![]() ;
;
![]() ;
;
![]() та
та
![]() навмання ставиться точка. Нехай
навмання ставиться точка. Нехай
![]()
![]() -
випадкові координати цієї точки.
Обчислити
-
випадкові координати цієї точки.
Обчислити
![]() ,
,
![]() .
.
4.2.15.
У прямокутник з вершинами
![]() ;
;
![]() ;
;
![]() та
та
![]() навмання ставиться точка. Нехай
навмання ставиться точка. Нехай
![]() -
випадкові координати цієї точки.
Обчислити
-
випадкові координати цієї точки.
Обчислити
![]() ,
,
![]() .
.
4.2.16.
У прямокутник з вершинами
![]() ;
;
![]() ;
;
![]() та
та
![]() навмання ставиться точка. Нехай
навмання ставиться точка. Нехай
![]() -
випадкові координати цієї точки.
Обчислити
-
випадкові координати цієї точки.
Обчислити
![]() ,
,
![]() .
.
4.2.17. Дискретні випадкові величини задані розподілами:
|
X |
-1 |
0 |
1 |
|
Y |
10 |
22 |
|
P |
0,1 |
0,2 |
0,7 |
|
P |
0,5 |
0,5 |
Знайти
закон розподілу випадкової величини
![]() .
.
4.2.18 Дискретні випадкові величини задані розподілами:
|
X |
-10 |
0 |
10 |
|
Y |
1 |
2 |
|
P |
0,6 |
0,1 |
0,3 |
|
P |
0,5 |
0,5 |
Знайти
закон розподілу випадкової величини
![]() .
.
4.2.19.
Випадкова величина
![]() має біноміальний закон розподілу
має біноміальний закон розподілу
![]() ,
,
![]() .
.
Обчислити
математичне сподівання та дисперсію
випадкової величини
![]() .
.
4.2.20. Дискретні випадкові величини задані розподілами:
|
X |
1 |
2 |
3 |
|
Y |
10 |
22 |
|
P |
0,3 |
0,1 |
0,6 |
|
P |
0,5 |
0,5 |
Знайти
закон розподілу випадкової величини
![]() .
.
ЗАВДАННЯ 4.3.
4.3.1. Закони розподілу числа очок, які вибиває кожен з двох стрілків:
|
X |
1 |
2 |
3 |
|
Y |
1 |
2 |
3 |
|
P |
0,1 |
0,3 |
0,6 |
|
P |
0,2 |
0,3 |
0,5 |
Знайти закон розподілу суми очок, які вибивають два стрілка.
4.3.2.
Двовимірна випадкова величина
![]() має щільність розподілу ймовірностей
має щільність розподілу ймовірностей
![]() .
.
Знайти
величину А та
функцію розподілу
![]() величини
величини
![]() .
.
4.3.3.
В умовах попередньої задачі знайти
ймовірність попадання випадкової точки
![]() у квадрат, обмежений прямими
у квадрат, обмежений прямими
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
4.3.4.
Випадкові величини
![]() і
і
![]() незалежні і нормально розподілені з
незалежні і нормально розподілені з
![]() ,
,
![]() .
Знайти ймовірність того, що випадкова
точка
.
Знайти ймовірність того, що випадкова
точка
![]() потрапить
в кільце
потрапить
в кільце
![]() .
.
4.3.5.
Знайти щільність ймовірності модуля
радіус вектора
![]() ,
якщо випадкові величини
,
якщо випадкові величини
![]() і
і
![]() незалежні і нормально розподілені з
незалежні і нормально розподілені з
![]() ,
,
![]() .
.
4.3.6.
Визначити щільність ймовірності системи
двох випадкових величин
![]() і
і
![]() за заданою функцією розподілу
за заданою функцією розподілу
![]()
4.3.7.
Випадкова точка
![]() на площині розподілена за наступним
законом:
на площині розподілена за наступним
законом:
-
X\Y
-1
0
1
0
0,1
0,15
0,2
1
0,15
0,25
0,15
Знайти
числові характеристики
![]() :
математичне сподівання, дисперсію,
коваріацію, коефіцієнт кореляції.
:
математичне сподівання, дисперсію,
коваріацію, коефіцієнт кореляції.
4.3.8.
Двовимірна випадкова величина
![]() розподілена зі щільністю
розподілена зі щільністю
![]() ,
в області
,
в області
![]() і
і
![]() по за межами області. Область
по за межами області. Область
![]() - трикутник, обмежений прямими
- трикутник, обмежений прямими
![]() ;
;
![]() ;
;
![]() .
Знайти: величину
.
Знайти: величину
![]() ,
математичне сподівання, дисперсію,
коваріацію, коефіцієнт кореляції.
,
математичне сподівання, дисперсію,
коваріацію, коефіцієнт кореляції.
4.3.9. Задано розподіл ймовірностей дискретної двовимірної випадкової величини:
-
Y\X
26
30
41
50
2,3
0,05
0,12
0,08
0,04
2,7
0,09
0,3
0,11
0,21
Знайти закони розподілу складових.
4.3.10.
Знайти ймовірність попадання випадкової
точки
![]() в прямокутник, обмежений прямими
в прямокутник, обмежений прямими
![]() ;
;
![]() ;
;![]() ;
;
![]() ,
якщо відома функція розподілу
,
якщо відома функція розподілу
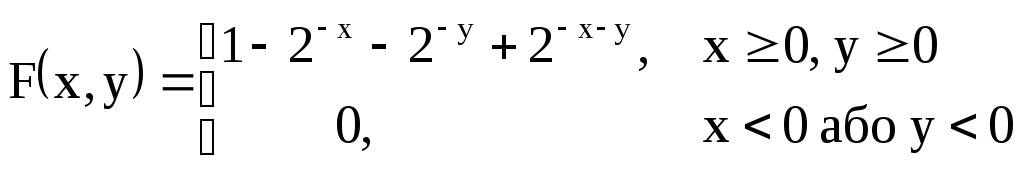 .
.
4.3.11.
Задана функція розподілу двовимірної
випадкової величини
![]()
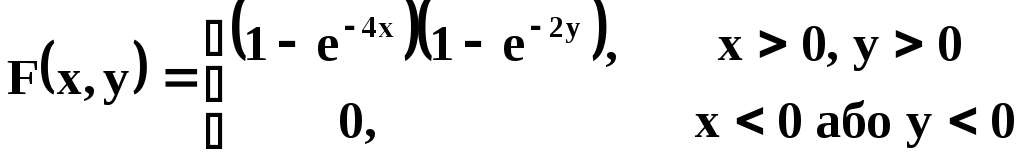
Знайти
двовимірну щільність ймовірності
системи
![]() .
.
4.3.12.
Задана двовимірна щільність
розподілу
системи
випадкових
величин
![]()
![]() .
.
Знайти
функцію
розподілу системи
![]() .
.
4.3.13.
Задана двовимірна щільність
розподілу
системи
випадкових
величин
![]()
![]()
в
квадраті
![]() ,
,
![]() ;
;
![]() по за межами квадрату.
по за межами квадрату.
Знайти
функцію
розподілу системи
![]() .
.
4.3.14.
Задана двовимірна щільність
розподілу
системи
випадкових
величин
![]()
![]()
Знайти
постійну
![]() .
.
4.3.15.
В першому квадранті задана функція
розподілу системи
випадкових
величин
![]()
![]()
Знайти
двовимірну щільність розподілу системи,
ймовірність попадання випадкової точки
![]() в трикутник з вершинами
в трикутник з вершинами
![]() ,
,
![]() ,
,
![]() .
.
4.3.16.
Щільність сумісного розподілу неперервної
двовимірної випадкової величини
![]()
![]() .
.
Знайти
постійну
![]() .
.
4.3.17.
Щільність сумісного розподілу неперервної
двовимірної випадкової величини
![]()
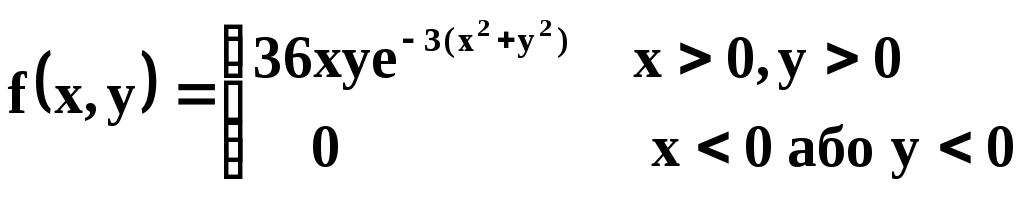 .
.
Знайти
математичне сподівання та дисперсію
складових
![]() і
і
![]()
4.3.18.
Щільність сумісного розподілу неперервної
двовимірної випадкової величини
![]()
![]() в квадраті
в квадраті![]() ,
,
![]() ;
;
![]() по за межами квадрату. Знайти математичне
сподівання складових
по за межами квадрату. Знайти математичне
сподівання складових
![]() і
і
![]()
4.3.19.
Щільність сумісного розподілу неперервної
двовимірної випадкової величини
![]()
![]() в квадраті
в квадраті![]() ,
,
![]() ;
;
![]() по за межами квадрату. Знайти математичне
сподівання та дисперсію складових
по за межами квадрату. Знайти математичне
сподівання та дисперсію складових
![]() і
і
![]()
4.3.20.
Щільність сумісного розподілу неперервної
двовимірної випадкової величини
![]()
![]() в квадраті
в квадраті![]() ,
,
![]() ;
;
![]() по за межами квадрату. Знайти математичне
сподівання та дисперсію складових
по за межами квадрату. Знайти математичне
сподівання та дисперсію складових
![]() і
і
![]() .
.
