
- •Содержание
- •Задание на расчетно-графическую работу
- •Постановка задачи и математическое моделирование объектов задания расчетно-графической работы. Описание методов исследования Теоретическое обоснование работы
- •Определение типа распределения с помощью критерия Пирсона ("хи-квадрат")
- •Критерий согласия Колмогорова
- •Практическая постановка задачи
- •Выполнение задания ргр
- •Список литературы
- •Приложение 1
Критерий согласия Колмогорова
Проверку гипотезы о законе распределения можно проводить с помощью критерия Колмогорова. Это альтернатива критерию хи-квадрат. Применение этого критерия не требует расчета ожидаемых частот и может использоваться для малых выборок. Данные должны представлять случайную выборку, переменные должны быть измерены по крайней мере на порядковой шкале; должна быть сформулирована гипотеза о распределении генеральной совокупности. Нулевая гипотеза состоит в том, что выборка взята из специфицированной генеральной совокупности. Альтернативная гипотеза заключается в утверждении обратного.
Критерий Колмогорова применяется для проверки гипотезы о непрерывной функции распределения случайной величины X.
Пусть заранее известно, что функция распределения исследуемой случайной величины X – непрерывная. Выдвинем гипотезу
![]() ,
,
то
есть предложение, что функцией
распределения случайной величины
является выбранная нами из каких-то
соображений непрерывная функция
![]() .
.
Требуется
принять или отклонить эту гипотезу по
реализации
![]() случайной
выборки
случайной
выборки![]() независимых
измерений X.
независимых
измерений X.
Для
решения этой задачи введем статистику
![]() критерия проверки гипотезы
критерия проверки гипотезы
![]() в
виде случайной величины:
в
виде случайной величины:
![]() ,
,
где
![]() - статистическая функция распределения.
- статистическая функция распределения.
Реализация
t
статистики
![]() ,
соответствующая выборке
,
соответствующая выборке
![]() ,
может быть найдена по формуле
,
может быть найдена по формуле
![]() (27.1)
(27.1)
где
![]() - реализация статистической функции
распределения
- реализация статистической функции
распределения
![]() .
.
Доказано,
что (H
– истинна)
![]() .
.
Здесь
D
– случайная величина, распределенная
по известному закону Колмогорова. Для
этой величины, используя таблицы или
формулы распределения Колмогорова,
можно найти
![]() из условия:
из условия:
![]() ,
,
где
![]() - вероятность практически невозможного
события, и, следовательно, событие
- вероятность практически невозможного
события, и, следовательно, событие
![]() - практически невозможное.
- практически невозможное.
Из
предыдущих соотношений следует: [H
- истинна]
![]() ,
то есть: [H
- истинна]
,
то есть: [H
- истинна]
![]() [
[![]() - практически невозможно].
- практически невозможно].
Теперь
с точностью до принципа практической
уверенности можно утверждать, что если
гипотеза Н истинна, то реализации t
статистики Т не могут превосходить
границы
![]() .
Далее по закону контрапозиции
математической логики находим, что с
той же точностью из неравенства
.
Далее по закону контрапозиции
математической логики находим, что с
той же точностью из неравенства
![]() следует ложность гипотезы Н. Итак, с
точностью до принципа практической
уверенности имеем:
следует ложность гипотезы Н. Итак, с
точностью до принципа практической
уверенности имеем:
(Н
– истинна)
![]() ;
;
![]() (Н
– ложна).
(Н
– ложна).
Из
этих соотношений следует, что неравенство![]() необходимо для принятия, а неравенство
необходимо для принятия, а неравенство
![]() достаточно для отклонения гипотезы Н
(с точностью до принципа практической
уверенности).
достаточно для отклонения гипотезы Н
(с точностью до принципа практической
уверенности).
Руководствуясь этими соображениями, принимают следующее правило решения поставленной задачи:
![]() (Н
– принять);
(Н
– принять);
(27.2)
![]() (Н
– отклонить);
(Н
– отклонить);
Правило (27.2) называют критерием согласия Колмогорова проверки гипотезы о непрерывной функции распределения случайной величины. Алгоритм его, очевидно, состоит в следующем:
-
Провести независимые n-кратные измерения случайной величины X с непрерывной функцией распределения и получить выборку
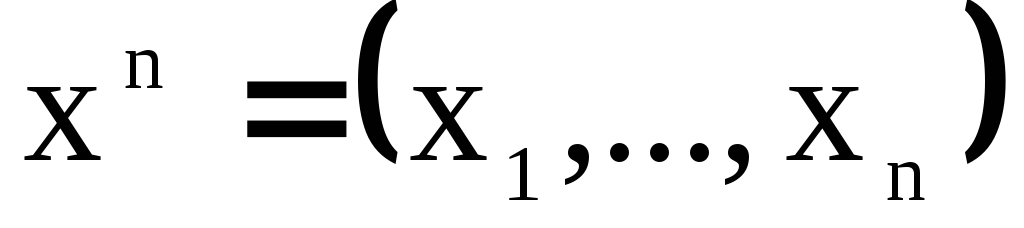 .
. -
Исключить из выборки грубые ошибки.
-
Построить реализацию
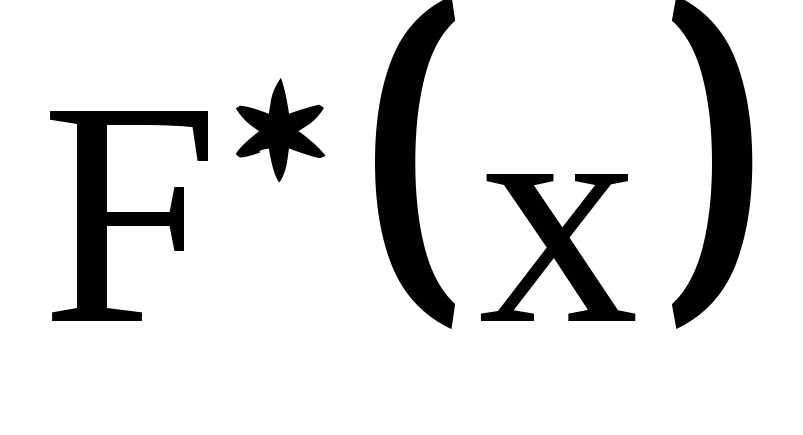 статистической функции распределения.
статистической функции распределения. -
Выдвинуть гипотезу
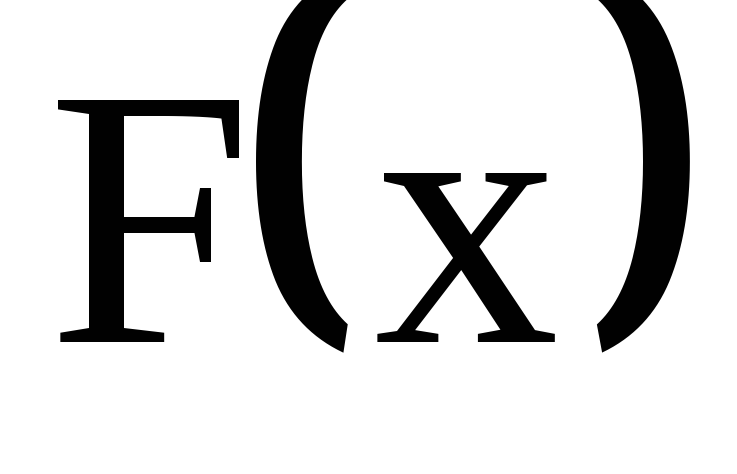 о функции распределения случайной
величины X.
о функции распределения случайной
величины X. -
Вычислить параметр t по формуле 27.1.
-
Задать вероятность
 практически невозможного события и из
таблиц распределения Колмогорова найти
параметр
практически невозможного события и из
таблиц распределения Колмогорова найти
параметр
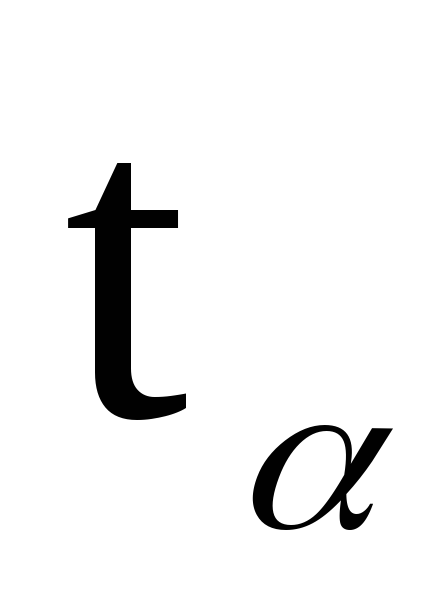 .
. -
Принять или отклонить гипотезу
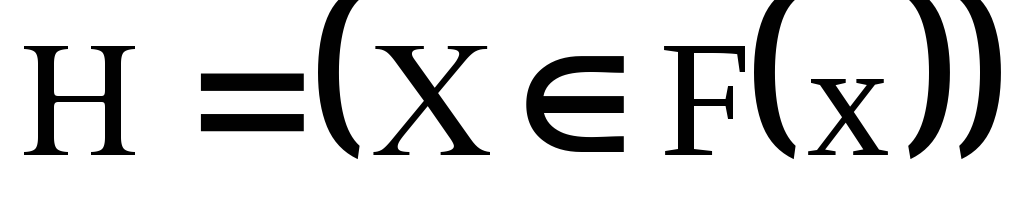 .
.
Доказано,
что критерий А. Н. Колмогорова состоятельный
и в общем случае смещенный. Он более
чувствителен к различию гипотез, поэтому
при прочих равных условиях может
применяться для меньших объемов выборки.
Поскольку результат проверки признака
критерия t
зависит от наибольших различий
![]() и
и
![]() ,
то нет необходимости построения
,
то нет необходимости построения
![]() и
и
![]() на всем диапазоне изменения x;
достаточно ограничиться областью
наибольших различий
на всем диапазоне изменения x;
достаточно ограничиться областью
наибольших различий
![]() и
и
![]() .
Недостатком критерия является то, что
точность его выводов нарушается, если
в формировании гипотезы об
.
Недостатком критерия является то, что
точность его выводов нарушается, если
в формировании гипотезы об
![]() используются характеристики эмпирических
распределений, так как в этом случае
статистика Т зависит от
используются характеристики эмпирических
распределений, так как в этом случае
статистика Т зависит от
![]() .
.
Следует
отметить значительную трудоемкость
построения статистики А. Н. Колмогорова,
однако, использование современных
компьютерных средств автоматизированных
вычислений преодолевает этот недостаток.
К достоинствам метода следует отнести
тот факт, что при построении статистики
А. Н. Колмогорова используется вся
информация, содержащаяся в выборке
![]() .
.
