Определение типа распределения с помощью критерия Пирсона ("хи-квадрат")

Критерий Пирсона основан на сравнении эмпирических (наблюдаемых) и теоретических (вычисленных на основе предполагаемого распределения) частот. Сравнение частот по критерию согласия позволяет на основе результатов экспериментов ответить на вопрос: случайно расхождение частот или неслучайно?

Возможно, что расхождение частот случайно (незначимо), и это объясняется либо малым числом наблюдений, либо способом их группировки, либо другими причинами. При этом эмпирические и теоретические частоты соответствуют предполагаемому распределению.

Возможно, что расхождение частот неслучайно (значимо), и объясняется тем, что эмпирические частоты не соответствуют предполагаемому теоретическому закону распределения.

Определение типа распределения можно разбить на два этапа.

• Выдвижение предположения о типе распределения.

• Проверка этого предположения.

В некоторых случаях на основе предыдущих исследований уже предполагается тип распределения, поэтому задача сводится только к его проверке.

Рассмотрим задачу проверки статистической гипотезы о нормальном распределении.

В общем случае исследование нормального закона распределения начинается с построения гистограммы.

1) Весь интервал наблюдаемых значений случайной величины Х – выборки объема n, делят на r частичных интервалов () одинаковой длины. Находят середины частичных интервалов . В качестве частоты варианты принимают число вариант, которые попали в j-ый интервал. В итоге получают последовательность равноотстоящих вариант и соответствующих им частот , сумма которых равна .

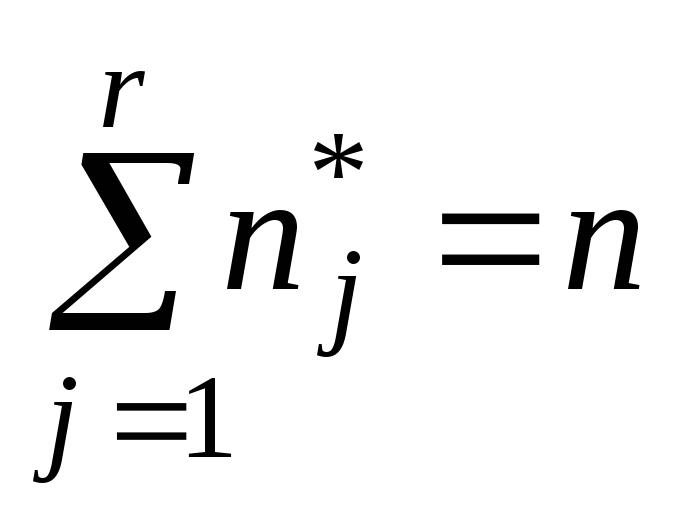2) Если основные параметры распределения m и неизвестны, то вместо них используют их выборочные оценки и . Вычисляют выборочную среднюю , выборочную дисперсию и нормируют случайную величину Х. Переходят к нормированной случайной величине и вычисляют концы интервалов ():

, ,

при этом наименьшее значение случайной величины Z , т.е.. , полагают равным «»,а наибольшее, т.е. , полагают равным «+».

3) Используя функцию Лапласа Ф(z) вычисляют теоретические вероятности попадания Х в интервалы () по равенству

и находят теоретические частоты . При этом необходимо следить, чтобы ≥ 5. Если это условие не соблюдается, то необходимо увеличить длину интервалов разбиения.

4) Для нахождения меры отклонения эмпирических частот от частот предполагаемого нормального распределения используется величина

,

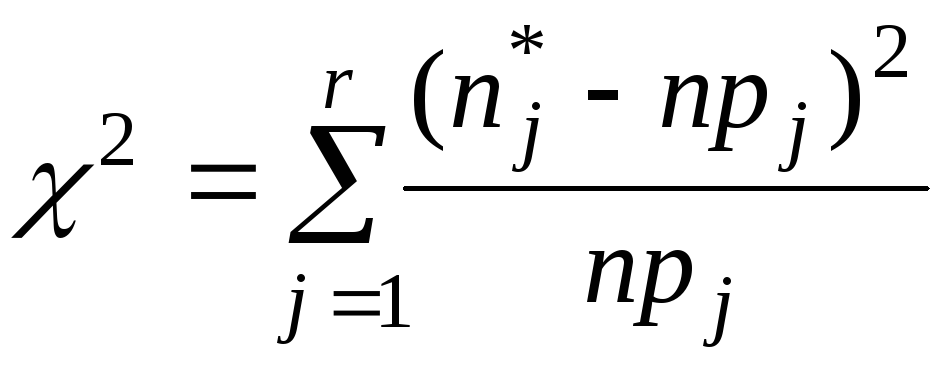которая распределена по закону «хи-квадрат» с числом степеней свободы , где r – число групп (частичных интервалов), а s – число параметров предполагаемого распределения (в частности, для нормального распределения s = 2 (параметры m и )). Если, например, предполагают, что генеральная совокупность распределена по закону Пуассона, то s = 1 (так как этот закон характеризуется параметром ). Для равномерного закона распределения s = 0.

Критерием проверки (значимости) служит сопоставление величины,

подсчитанной для значений частот с табличным значением , которое соответствует заданному уровню значимости ε и числу степеней свободы k = r – 3.

Если окажется, что < , то говорят, что данные не противоречат выдвинутой гипотезе о нормальном распределении случайной величины Х. В противном случае этого утверждать нельзя, так как распределение существенно отличается от предполагаемого.

Необходимо отметить, что величина имеет «хи-квадрат» распределение при достаточно больших n , однако удовлетворительные результаты при проверке гипотезы получаются уже при n > 100 .