
Задание 3
Пример. Производится 4 независимых выстрела по мишени с вероятностью попадания 0,6 при каждом выстреле. X – число попаданий в мишень. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность попадания в мишень не менее двух раз.
Решение. а)
Дискретная
случайная величина X,
представляющая собой число попаданий
в мишень при 4 выстрелах, имеет следующие
возможные значения:
![]() .
Поскольку испытания независимы и при
каждом испытании вероятность появления
события А
одна и та же, то для определения
соответствующих вероятностей применима
формула Бернулли
.
Поскольку испытания независимы и при
каждом испытании вероятность появления
события А
одна и та же, то для определения
соответствующих вероятностей применима
формула Бернулли
![]()
![]()
По условию задачи
![]() .
Следовательно
.
Следовательно
![]() .
Тогда
.
Тогда

Составим ряд распределения случайной величины Х:
|
X |
0 |
1 |
2 |
3 |
4 |
|
P |
0,0123 |
0,0988 |
0,2963 |
0,3951 |
0,1975 |
Для контроля над
правильностью вычисления вероятностей,
найдем суму вероятностей, которая должна
быть равна единице:
![]() .
.
Найдем функцию распределения случайной величины Х:
-
если
 ,
то
,
то
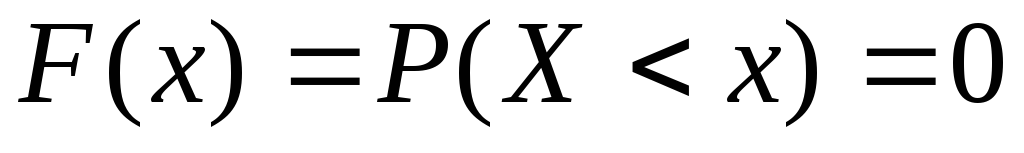 ,
так как значений, меньших числа 0,
величина Х
не принимает;
,
так как значений, меньших числа 0,
величина Х
не принимает;
-
если
 ,
то
,
то
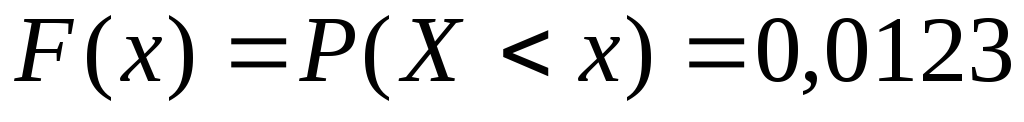 ,
так как величина Х
может принять значение 0 с вероятностью
0,0123;
,
так как величина Х
может принять значение 0 с вероятностью
0,0123;
-
если
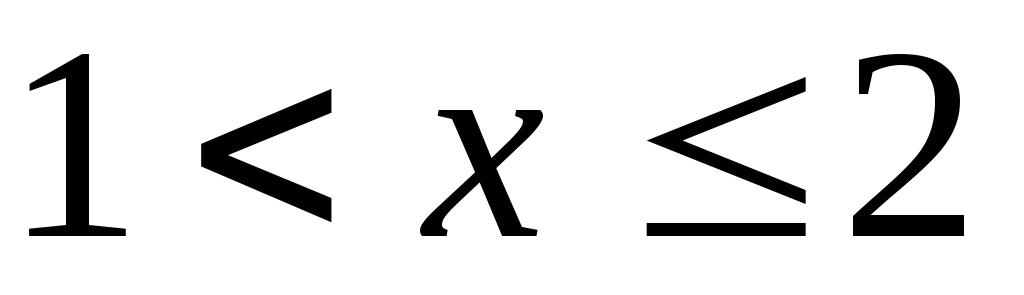 ,
то
,
то
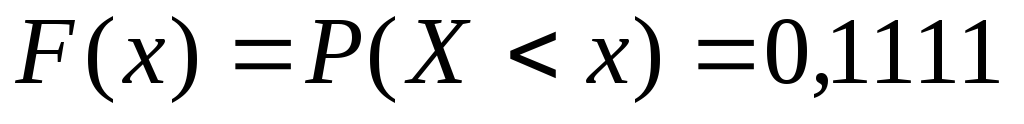 ,
так как в этом случае величина Х
может принять значение 0 или 1, и по
теореме сложения вероятностей
несовместных событий имеем
,
так как в этом случае величина Х
может принять значение 0 или 1, и по
теореме сложения вероятностей
несовместных событий имеем
![]() ;
;
-
если
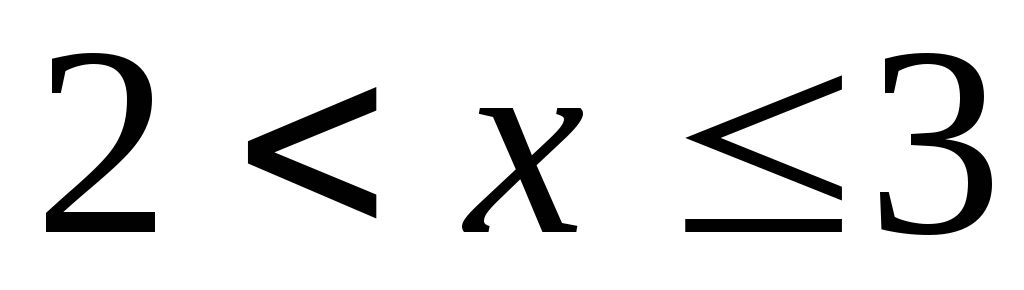 ,
то
,
то
![]() ;
;
-
если
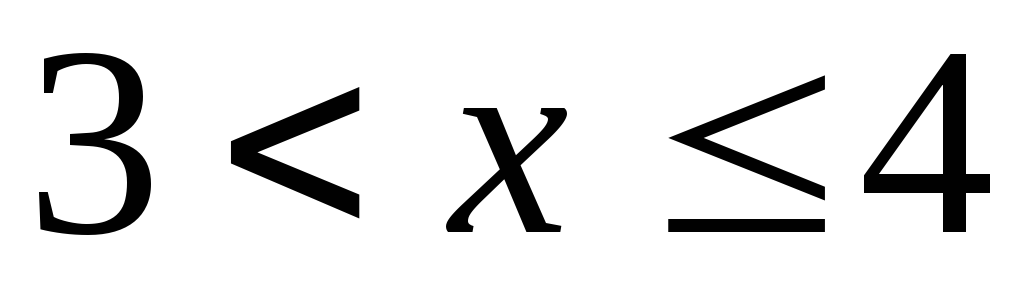 ,
то
,
то
![]() ;
;
-
если
 ,
то
,
то
 ,
так как событие
,
так как событие
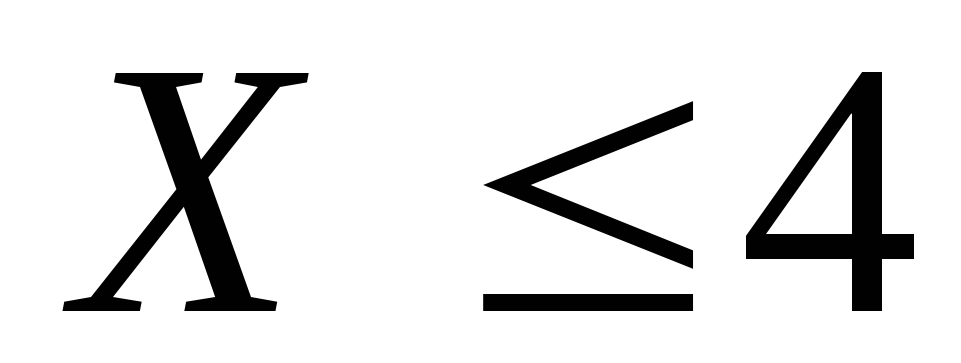 достоверное и вероятность его равна
единице.
достоверное и вероятность его равна
единице.
Итак, искомая функция распределения имеет вид

б) Математическое ожидание случайной величины Х найдем, исходя из его определения:
![]() .
.
Дисперсию можно вычислить исходя из ее определения, но мы воспользуемся формулой, которая значительно упрощает вычисления
![]() .
.
Найдем математическое
ожидание случайной величины
![]() :
:
![]()
Тогда
![]() .
.
Найдем среднее квадратическое отклонение
![]() .
.
Вероятность попадания в мишень не менее двух раз в серии из 4 выстрелов найдем следующим образом:
![]() .
.
-
Производится 3 независимых выстрела по мишени с вероятностью попадания 2/3 при каждом выстреле. X – число попаданий в мишень. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность хотя бы одного промаха.
-
Производится 3 выстрела по мишени. Вероятность попадания при первом, втором и третьем выстрелах соответственно равны 0,4; 0,5 и 0,7. X – число попаданий в мишень. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность не менее трех попаданий в мишень.
-
В некотором цехе брак составляет 5% всех изделий. Х – число бракованных изделий из трех взятых на проверку. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность того, что среди этих 3 изделий будет не менее 2 бракованных.
-
Производится 2 независимых выстрела с вероятностями попадания в цель соответственно 0,6 и 0,5. X – число попаданий в мишень. Для этой случайной величины: а) построить ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность поражения цели.
-
Станок штампует детали. Вероятность того, что изготовленная деталь окажется стандартной, равна 0,9. Х – число стандартных деталей среди четырех проверяемых. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность того, что среди этих четырех деталей бракованных будет не менее трех.
-
Вероятность появления события А в одном испытании равна 2/3. X – число появлений события А в трех независимых испытаниях. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность хотя бы двух появлений события А в трех испытаниях.
-
Производится 3 выстрела по мишени. Вероятности попадания при каждом выстреле равны 3/4. X – число попаданий в мишень. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность двух попаданий в мишень.
-
Х – число выпадений шестерки при четырех подбрасываниях игральной кости. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность невыпадения шестерки при четырех подбрасываниях кости.
-
Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,8. X – число стандартных изделий среди четырех проверенных. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность не менее трех бракованных изделий среди этих четырех.
-
Станок-автомат штампует детали. Вероятность того, что не будет выпущено ни одной бракованной детали, равна 0,98. Х – число стандартных деталей среди трех проверенных. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность того, что среди этих трех деталей будет хотя бы две бракованных.
-
X – число выпадений решки при трех подбрасываниях монеты. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность выпадения трех гербов.
-
Устройство состоит из четырех элементов. Вероятность того, что за время опыта любой из этих элементов откажет, равна 0,1. X – число отказавших элементов. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность отказа не менее двух элементов.
-
Бросают три игральные кости. Тройка выпала Х раз. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность выпадения двух троек.
-
Производится 5 независимых выстрелов с вероятностью попадания 0,2 при каждом выстреле. Х – число попаданий в мишень. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность не менее 3 попаданий в мишень.
-
Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,1. Х – число бракованных деталей из трех взятых на проверку. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность того, что среди этих 3 деталей будет не более одной бракованной.
-
Вероятность появления события А в одном испытании равна 1/3. Х – число появлений события А в четырех испытаниях. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность появления события А хотя бы в двух испытаниях.
-
X – число выпадений герба при четырех подбрасываниях монеты. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность выпадения трех гербов.
-
Производится 4 выстрела по мишени. Вероятности попадания при каждом выстреле равны 0,6. X – число попаданий в мишень. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность двух попаданий в мишень.
-
Производится испытание детали на надежность. Вероятность отказа детали за время испытания равна 0,3. Х – число отказавших деталей из трех, подвергнувшихся испытанию. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность отказа не более одной детали.
-
Игральную кость подбрасывали три раза. X – число выпадений двойки. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность не более двух выпадений двойки.
-
Станок-автомат штампует детали. Вероятность того, что изготовленная деталь окажется бракованной, равна 0,2. Х – число бракованных деталей из 5 взятых на проверку. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность того, что среди этих 3 деталей будет не более одной бракованной.
-
Производится 3 выстрела по мишени. Вероятности попадания при каждом выстреле равны 3/4. X – число попаданий в мишень. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность двух попаданий в мишень.
-
Устройство состоит из трех элементов. Вероятность того, что за время опыта любой из них откажет, равна 0,2. X – число отказавших элементов. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность отказа не более одного элемента.
-
В партии 10% нестандартных деталей. Наудачу отобраны 4 детали. Х – число стандартных среди них. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность того, что среди этих четырех деталей бракованных будет не менее трех.
-
Две игральные кости одновременно бросают 2 раза. X – число выпадений четного числа очков на двух игральных костях. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность не более двух выпадений четного числа очков.
-
Вероятность выхода за границу поля допуска при обработке плунжера на токарном станке равна 0,07. Для проверки наудачу отобрано 3 плунжера. Х – число деталей, размеры которых не соответствуют заданному допуску. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность того, что среди отобранных для проверки плунжеров не соответствуют заданному допуску размеры не более чем у двух плунжеров.
-
Станок штампует детали. Вероятность того, что изготовленная деталь окажется стандартной, равна 0,8. Х – число стандартных деталей среди 5 проверяемых. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность того, что среди этих 5 деталей бракованных будет не менее трех.
-
Х раз выпадает герб при пяти подбрасываниях монеты. Для этой случайной величины: а) построить ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность не менее трех выпадений герба.
-
Игральную кость подбрасывали четыре раза. X – число выпадений шести очков. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность не более двух выпадений шести очков.
-
Вероятность появления события А в одном испытании равна 1/4. Произведено четыре испытания. Событие А появилось в них Х раз. Для этой случайной величины: а) найти ряд и функцию распределения; б) найти математическое ожидание, среднее квадратичное отклонение, вероятность появления события А хотя бы в двух испытаниях.
