1.2. Уравнения максвелла в интегро-дифференциальной формах и их физический смысл

1.2.1.Электромагнитное поле

Электромагнитное поле (ЭМП) есть особый вид материи, обладающий массой и энергией. Энергия ЭМП проявляется на макроскопическом и микроскопическом уровнях. Эти проявления совершенно разнятся описываемыми свойствами ЭМП. Поэтому в науке образовано два направления при решении электродинамических задач [1-6]. Первое направление имеет название КЛАССИЧЕСКОЙ ЭЛЕКТРОДИНАМИКИ, в которой единое и неделимое поле представляется в виде магнитной и электрической составляющих. Данное направление отвоевало свое существование в науке опытами Ампера и Фарадея, которыми установлено действие электрической составляющей на неподвижный заряд и магнитной – на рамку с током. Второе направление названо КВАНТОВОЙ ЭЛЕКТРОДИНАМИКОЙ, в которой затрагивается микроструктура, то есть ЭМП есть поток фотонов - мельчайших частиц, обладающих массой и энергией. Причем излучение фотонов происходит возбужденным электроном, попавшим в тормозящее поле. Будущее за квантовой электродинамикой. Пока же классическая электродинамика является основой теории и практики распространения волн и антенн. Поэтому изучение дисциплины происходит с позиции классической электродинамики.

1.2.2. Описание электромагнитного поля

Электромагнитное поле может быть описано четырьмя векторными величинами: вектор электрического поля – Е, вектор электрического смещения – D, вектор магнитного поля - H, вектор магнитной индукции - В. Определить поле в любой области пространства - значит указать эти векторы для любой ее точки как совокупность электрических Е и D и магнитных Н и В составляющих [1-6].

Вектор Е характеризует напряженность электрического поля как силовое действие F электрического поля на единицу положительного заряда Q

F (ньютон)

Е = l i m ----------------- , (В / м). (1.1)

^{Q → 0} Q (кулон)

П Р И М Е Р.

Вектор Е, или напряженность электрического поля, создаваемая зарядом, прямо пропорциональна величине заряда и обратно пропорциональна квадрату расстояния ( r ) до точки наблюдения [12]

Q

E = ---------------- r, (В / м), (1.2)

4 π ε r ³

где ε -диэлектрическая проницаемость среды, причем ε = ε ₁ ε ₀;

ε₁ – относительная диэлектрическая проницаемость среды,

например - ε₁ = 1 – для вакуума,

ε ₁ = 5 – 10 -- для стекла;

ε ₀ – электрическая постоянная вакуума имеет значение

Q

ε ₀ = ----------- = 10 ^{– 9} / 36 π , (Ф / м). (1.3)

E dS

Вектор электрического смещения D, который в однородных и изотропных средах пропорционален напряженности электрического поля Е

D = ε ₀ E , (К / м ²). (1.4)

П Р И М Е Р.

Вектор D для заряда не зависит от диэлектрической проницаемости

среды [12]

Q

D = --------- r, (К / м) . (1.5)

4 π r ³

Для любой среды D зависит от вектора поляризации Р

Р

(Р = l i m ---, К/м²) вещества среды.

^V→0 V

D = ε ₀ E + P , (1.6)

где Р - электрический момент диполя обьемом V.

Вектор Н характеризует напряженности магнитного поля:

- в вакууме

Н = В / μ ₀ , А / м; (1.7)

- для среды

Н = В / μ ₀ - М, (1.8)

где μ ₀ = 4π 10 ^{-- 7} , ГН / м --магнитная постоянная (1.9)

вакуума;

М - намагниченность среды, равная

Σ М

М = l i m ---------, А / м; (1.10)

^v→0 V

ΣΜ – магнитный момент объема V.

Вектор В, вектор магнитной индукции, характеризующий силовое воздействие магнитного поля на движущийся заряд

F ( ньютон )

B = ------------------------, Вебер / м ² , (1.11)

Q V ( кулон, м / с )

где V – вектор скорости.

Если направление движения V заряда Q совпадает с направлением действия вектора В, то силовое воздействие F равно нулю ( F = 0 ). Если же между В и V угол равен 90 ⁰, то силовое воздействие F максимально (рис. 1.1).

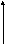
B

Q V

F

Рис. 1.1

1.2.3.Электрический заряд

Электрические заряды можно считать бесконечно делимыми и пользоваться понятием плотности заряда. Если заряд Q распределен в пространстве V, то объемная плотность заряда ρ равна

d Q

ρ = ---------- . (1.12)

d V

Cоответственно, заряд определится

Q = ∫ ρ dV. (1.13)

^v

Если заряд Q распределен по поверхности S, то поверхностная плотность заряда g dQ

g = ------ , (1.14)

dS

а заряд определится

Q = ∫ g dS . (1.15)

^s

Линейная плотность заряда τ

d Q

на длине d l τ = -------- . (1.16)

d l

Зная точечные заряды dQ, можно определить распределенный в пространстве потенциал dφ и напряженность электрического поля dе

dQ dQ

dφ = ----------; dе = ---------- r. (1.17)

4 π ε ґ 4 π ε ґ ²

Складывая dφ , можно определить φ dQ

φ = ∫ dφ = ∫ ------- . (1.18)

4π ε ґ

Напряженность поля Е

Е = ∫ dе, где е = - grad φ. (1.19)

Если размеры заряженного тела малы по сравнению с расстоянием от него до точек, в которых рассматривается поле, то заряд такого тела называется точечным. Форма тела не оказывает влияние на поле, если источник точечный. Неподвижный заряд создает электрическое поле, называемое электростатическим.

4. Электрический ток

Электрический ток в проводящей среде есть упорядоченное движение электрических зарядов под действием сил поля [11]. Такой ток называют током проводимости. Плотность тока проводимости δ пропорциональна напряженности электрического поля Е и зависит от проводимости среды σ

δ = σ Е , (1.20)

где - σ = 1 / R, См/ м;

- R есть активное сопротивление среды, Ом.

Если заряды ρ движутся в вакууме со скоростью ν, то они образуют ТОК ПЕРЕНОСА . Плотность тока переноса δ _пер

δ _пер = ρ ν. (1.21)

В диэлектрике, который вносится во внешнее поле, под действием сил поля связанные заряды будут смещаться и создадут ТОК ПОЛЯРИЗАЦИИ. Плотность тока поляризации δ_поляр пропорциональна скорости изменения вектора поляризации Р ∂ Р

δ _поляр = ------ . (1.22)

∂ t

Все три перечисленных вида тока представляют собой перемещение зарядов. Каждый из этих токов сопровождается магнитным полем. МАКСВЕЛЛ предложил называть электрическим током изменение во времени электрического поля в вакууме, так при этом образуется магнитное поле. Этот ток называют током смещения. Плотность тока смещения δ_см^о пропорциональна скорости изменения напряженности электрического поля Е

∂ Е

δ _см^о = ε ------ . (1.23)

∂ t

Таким образом, полным электрическим током называют совокупность всех явлений, при которых образуется магнитное поле. Плотность полного тока δ_полн равна сумме плотностей тока проводимости, переноса, поляризации и смещения в вакууме

δ_полн = δ + δ_пер + δ_поляр + δ_см^о. (1.24 )

Сумму тока поляризации и тока смещения в вакууме называют током смещения в диэлектрике. Поэтому плотность тока смещения в диэлектрике равна

∂ Е ∂ D

δ_см = δ_поляр + δ_см^о = ε ----- = ----- . (1.25)

∂ t ∂ t

Току смещения присуще свойство распространяться в диэлектрике так же,

как току проводимости присуще свойство распространяться по проводнику. Ток переноса, как правило, не учитывается. Поэтому плотность полного тока есть сумма плотности тока проводимости и тока смещения. Плотность полного тока в этом случае ∂ E

δ_полн = δ + δ_см = σΕ + ε -----. (1.26)

∂ t

Полный ток может возникнуть как в проводящей, так и в непроводящей среде. В хорошо проводящей среде токи проводимости настолько больше токов смещения, что последними пренебрегают. В диэлектрике, с малыми потерями, токи смещения значительно больше токов проводимости и поэтому токи проводимости можно не учитывать. Как следствие, существуют диэлектрические и металлические излучатели. В полупроводящей среде могут существовать токи как проводимости, так и смещения, поэтому обе составляющие должны быть учтены.

1.2.5. Электромагнитные свойства сред

Связь векторов поля в материальной среде описывается уравнениями, которые получили название материальных уравнений

D = ε Е; В = μ Н; δ = σ Е . (1.27)

Макроскопические параметры ε , μ и σ в большинстве случаев не зависят от векторов поля. Соотношения (1.27) оказываются при этом линейными. Соответственно этому употребляется выражение линейные среды. Однако существуют среды, которые имеют технически важное значение и отличаются заметной зависимостью макроскопических параметров от векторов поля. Их называют нелинейными. Так, в устройствах сверхвысоких частот используются ферромагнетики - вещества, магнитная проницаемость которых значительна и сложным образом зависит от магнитного поля. Аналогично сегнетоэлектрики обладают зависимостью диэлектрической проницаемости от электрического поля. Зависимость степени электропроводности веществ делит их на проводники и диэлектрики. Промежуточная область принадлежит полупроводникам. Как правило, в электродинамике при анализе используют идеальные, воображаемые среды, называемые идеальный проводник (σ = ∞) и идеальный диэлектрик (σ = 0).

В электродинамике среды принимаются изотропными, то есть свойства сред одинаковы для полей любых направлений. В уравнениях (1.27) векторы E и D, H и B, а также δ и Ε в этих средах параллельны. Учитывая изотропность среды, можно записать одно из уравнений (1.27) например, тремя скалярными

В_х = μ Н_х; В_у = μ Н_у; В_z = μ Н_z , (1.28)

при этом очевидно, что функционально связаны только одноименные проекции векторов (В и Н). Однако существуют среды, проявляющие разные свойства в зависимости от направления поля, они называются анизотропными. Если анизотропия проявляется в магнитном поле , то вместо (1.28) будем иметь:

В_х = μ _хх Η _х + μ _ху Η _у + μ _хz H _z;

B _у = μ _ух Н _х + μ _уу Н _у + μ _уz Н _z; (1.29)

В _z = μ _zx Н _x + μ _zy Н _y + μ _zz Н _z.

В системе (1.29) каждая проекция вектора В зависит от трех проекций Н. Следовательно, векторы В и Н уже не параллельны. А всю совокупность действий, производимых над проекциями векторов В и Н, обозначают оператором

μ _{х х} μ _{х у} μ _{х z}

μ = μ _{у х} μ _{у у} μ _{у z} (1.30)

μ _{z х} μ _{z у} μ _{z z}

В результате, с учетом оператора (1.30) уравнение сохраняет форму (1.27)

В = μ Н. (1.31)

Оператор μ (1.30) называется тензором магнитной проницаемости, а его коэффициенты при проекциях Н – его компонентами. Совершенно аналогично описывается анизотропия диэлектрических свойств и проводимости

D = ε Ε ; δ = σ Ε . (1.32)

Существует понятие об однородности и неоднородности сред. Так в неоднородных средах параметры μ, ε и σ изменяются от точки к точке и могут быть представлены как функции пространственных координат. За небольшим исключением, в последующем будем рассматривать лишь линейные, однородные и изотропные среды.

1.2.6.Интегральная форма уравнений Максвелла

Первое уравнение Максвелла

Первое уравнение Максвелла явилось следствием законов Ампера и Био-Савара, установивших связь электрических и магнитных явлений[1-6]. Эта связь определена законом полного тока, который имеет вид

∫ Н dl = I _полн . (1.33)

L

В правой части уравнения (1.33) I _полн есть полный ток проводимости. Если известно сечение проводника, то несложно выразить полный ток проводимости через плотность проводимости δ

I _полн = ∫ δ ds. (1.34)

^S

В левой части уравнения (1.33) приведено описание магнитного поля в области окружающей проводник с полным током I _полн . Рассмотрим замкнутую цепь

с источником переменного тока U и чисто активным сопротивлением R (рис.1.2). Выражение (1.33) описывает физический процесс возникновения

магнитного поля Н при протекании в проводнике тока проводимости I _полн .

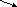Контур L Н

U ~ Н R

I

Рис.1.2

Однако выражение не отражает физического процесса для схемы электрической цепи рисунка 1.3, где дополнительно включен конденсатор С, причем только для участка разрыва цепи, которую создал сам конденсатор.

Контур L

С

R

U~ Н

I ~

Амперметр

Рис.1.3

Эта схема отображает физическое явление, при котором проявляет себя ток смещения I _см в цепи. Если использовать источник постоянного тока U=, то в цепи не будет протекать ток. Это объясняется тем, что в цепь включен конденсатор С, создающий для постоянного тока разрыв цепи. Следовательно, амперметр не покажет наличие тока. При включении же в цепь источника переменного тока U~, вместо постоянного тока U=, амперметр покажет наличие тока. Объяснить это можно появлением тока смещения I_см . На основании выражения (1.25) ток смещения зависит от скорости изменения потока вектора электрического смещения D через поверхность S

∂ D

I _см. = ∫ -------- d s. (1.35)

^S ∂ t

Рассмотренный пример явился обоснованием того, что закон полного тока, приведенный выражениями (1.33) и (1.34), не учитывает тока смещения I _см . Гениальность Максвелла состоит в том, что он, интуитивно, введя в выражение (1.33) для полного тока Био-Савара ток смещения, получил новое выражение, которое получило наименование первого уравнения Максвелла

∂D

∫Н dl = ∫ [ δ + ------- ] ds . (1.36)

^{L S} ∂ t

Первое уравнение Максвелла имеет следующее определение:

ЦИРКУЛЯЦИЯ ВЕКТОРА НАПРЯЖЕННОСТИ МАГНИТНОГО ПОЛЯ Н, ПО ЗАМ-

КНУТОМУ КОНТУРУ L, РАВНА ПОТОКУ ВЕКТОРА ПЛОТНОСТИ ТОКА ПРОВО-

ДИМОСТИ Δ И СКОРОСТИ ИЗМЕНЕНИЯ ПОТОКА ВЕКТОРА ЭЛЕКТРИЧЕСКО-

ГО СМЕЩЕНИЯ D, ЧЕРЕЗ ПОВЕРХНОСТЬ S, ОПИРАЮЩУЮСЯ НА ЭТОТ КОН-

ТУР L .

Физическое отображение первого уравнения Максвелла показано на рисунке 1.4.

Поверхность S n

ds

Контур L dl

dl

Линии плотности полного тока Н

δ _полн. = δ + δ _см

Рис.1.4

Физический смысл первого уравнения Максвелла несложно установить, используя выражение (1.36), определение и рисунок 1.4.

1. Первое уравнение есть закон полного тока Ампера - Максвелла, установленный для любой среды.

2. Для переменных токов источником поля являются ток проводимости и ток смещения.

3. Устанавливается связь между источником, которым является полный ток в виде δ _полн = δ + δ _см, и одним из векторов электромагнитного поля, а точнее, с вектором магнитного поля Н.

4. Для источника постоянного тока в цепи будет протекать только ток проводимости δ, который создаст вектор постоянного магнитного поля Н, такое поле называется полем стационарным. Стационарное магнитное поле создается постоянным током, протекаемым по виткам провода катушки.

Второе уравнение Максвелла

Второе уравнение получено Максвеллом на основании закона электромагнитной индукции, установленного Фарадеем [1-6]. Максвелл применил закон к любой среде. Физический смысл уяснится на приведенном рисунке 1.5.

∂ В

-----

∂t

Поверхность S

n

ds

d l

Контур L

dl Е

Линии векторов скорости изменения магнитной

индукции ∂ В / ∂ t

Рис.1.5

Закон электромагнитной индукции Фарадея гласит: если контур проводника пронизывает магнитный поток Ф, то наведенная электродвижущая сила U в контуре равна скорости изменения этого потока

∂ Ф

U = - ----- . (1.37)

∂t

Известно, что поток магнитной индукции Ф через поверхность S равен

_∞

Ф = l i m ∑ В d s = ∫В ds . (1.38)

^{n→ ∞ n S}

Но электродвижущая сила U в контуре L равна сумме векторов Е, действующих в этом контуре

_∞

U = l i m ∑ E d l = ∫Е d l . (1.39)

^{n→ ∞ n L}

Подставив в выражение (1.37), описывающее закон Фарадея, параметры Ф и U из выражений (1.38) и (1.39), получим второе уравнение Максвелла

∂

∫ Е d l = -- ----- ∫В d s . (1.40)

^L ∂ t ^S

Второе уравнение Максвелла читается следующим образом:

циркуляция вектора напряженности электрического поля Е по замкнутому контуру l равна взятой с обратным знаком скорости изменения во времени потока вектора магнитной индукции через поверхность s, опирающуюся на данный контур l.

Физический смысл второго уравнения Максвелла устанавливается по физической (рис. 1.5) и математической (выражение 1.40) моделям.

1. Уравнение может быть реализовано для любого контура L, где возможно

действие изменяющегося во времени потока магнитной индукции В.

2. Установлена связь между векторами магнитного Н (B = μ Η) и электри-

ческого Е полей как между составляющими единого, неделимого

электромагнитного поля.

3. В уравнение не входит источник, следовательно, выражение описывает

двигающееся электромагнитное поле или радиоволну.

4. Уравнение устанавливает, что всякое изменение магнитного поля во

времени приводит к изменению электрического поля в пространстве.

4. Электрическое поле, созданное меняющимся во времени магнитным

полем, имеет вихревой характер.

4. Электрические замкнутые линии поля охватываю собой вихри линий

переменного магнитного поля.

Третье уравнение Максвелла

В качестве третьего уравнения Максвелла используют уравнение Остроградского – Гаусса

∫ D ds = ∫ ρ dv . (1.41)

^{S V}

Уравнение взято как аксиома и читается следующим образом:

поток вектора электрического смещения D, через произвольную замкнутую поверхность S, равен полному заряду ρ в объеме V, ограниченном этой поверхностью S.

Физическая модель третьего уравнения показана на рисунках 1.6 и 1.7.

n D D

n

Объем V

d s Поверхность S ds

ρ

V

Поверхность S

Рис.1.6 Рис.1.7

На основании математической (выражение 1.41) и физической (рис.1.6 и 1.7) моделей ниже рассмотрен физический смысл третьего уравнения Максвелла.

1. Уравнение показывает, что при наличии в объеме V электрических зарядов

ρ в окружающем объем пространстве возникает электрическое поле

D = ε Ε (рис.1.6).

2. Если в объеме сосредоточены положительные заряды, такой объем назван истоком электрического поля и в окружающем его пространстве существуют силовые линии D, направленные от объема V, если же в объеме отрицательные заряды, то объем является стоком электрического поля.

3. Если суммарный заряд в объеме равен нулю (рис.1.7), то и поток вектора

электрического поля D равен нулю. Это означает, что количество линий поля, входящих в объем, равен числу силовых линий, выходящих из объема. Математическая запись этого случая следующая:

∫ D ds = 0. (1.42)

^S

Таким образом, источники электрического поля находятся в тех местах, в которых имеются электрические заряды.

Четвертое уравнение Максвелла

В качестве четвертого уравнения Максвелл использует уравнение Остроградского – Гаусса

∫ В d s = 0. (1.43)

^S

Математическая запись четвертого уравнения Максвелла утверждает:

поток вектора магнитной индукции B, через любую замкнутую поверхность S, равен нулю.

Физическая модель четвертого уравнения совпадает с физической моделью, приведенной на рисунке 1.7. Отличие состоит только в необходимой замене вектора D на B. Этим же и отличаются выражения (1.42) и (1.43).

Физический смысл четвертого уравнения Максвелла.

1. Магнитных зарядов в природе не существует.

2. Магнитное поле всегда вихревое.

3. Линии магнитного поля всегда замкнуты, то есть сколько линий поля вошло в замкнутую поверхность, столько линий и вышло из нее.

1.2.7. Дифференциальная форма уравнений Максвелла

Уравнения Максвелла в интегральной форме, приведенные выражениями (1.36), (1.40), (1.41) и (1.43), дают простой и ясный физический смысл по характеристике поля в объеме и на поверхности. Но для того, чтобы знать напряженность поля в любой точке пространства, пользуются дифференциальной формой уравнений Максвелла. Для приведения интегральной формы в дифференциальную воспользуемся:

• уравнением СТОКСА, которое устанавливает связь между линейным и поверхностным интегралами:

∫Е dl = ∫rot E ds или ∫Н dl = ∫rot Н ds, (1.44)

^{L S L S}

- уравнением ОСТРОГРАДСКОГО – ГАУССА, которое устанавливает связь

между поверхностным и объемным интегралами:

∫В ds = ∫div В dv или ∫D ds = ∫div D dv . (1.45)

^{S V S V}

Подставив выражения (1.44) и (1.45) в интегральную форму уравнений Максвелла, представленную выражениями (1.36), (1.40), (1.41) и (1.43), а также после незначительных преобразований, можно получить дифференциальную форму уравнений в следующем виде:

∂D

rot Н = δ + -----;

∂ t

∂B

rot Е = - -----;

∂ t (1.46)

div D = ρ;

div B = 0.

Уравнения Максвелла в дифференциальной форме, представленные выражениями (1.46), так же, как и в интегральной форме, дают описание взаимосвязи между векторами поля в любой точке пространства, где эти векторы в силу непрерывности параметров сред сами непрерывны.