Итоговый экзамен по курсу для всех форм обучения. Индексы комплектов мию22, мию11. Список тем по математике, выносимых на итоговый экзамен (комплекты мию22, мию11).

1. Теория множеств.

1. Способы задания множеств.

2. Диаграммы Эйлера-Венна

3. Основные операции над множествами

4. Свойства операций над множествами.

5. Декартово произведение множеств. Функция.

6. Мощность множеств.

2. Математическая логика.

1. Множество высказываний.

2. Основные операции над высказываниями.

3. Свойства операций над высказываниями.

4. Таблицы истинности.

5. Предикаты. Область истинности предиката.

6. Кванторы. Кванторные высказывания.

3. Комбинаторика.

1. Упорядоченные и неупорядоченные выборки.

2. Факториал. Свойства факториала.

3. Сочетания. Число сочетаний.

4. Свойства сочетаний.

5. Треугольник Паскаля и бином Ньютона.

6. Выборки из нескольких множеств. Правило суммы и правило произведения.

7. Упорядоченные выборки. Размещения. Число размещений.

8. Перестановки.

9. Размещения с повторениями.

4. Теория вероятностей.

1. Основные определения. Испытания. Множество событий. Случайная величина.

2. Сумма и произведение событий. Достоверное и невозможное события.

3. Полная группа событий. Элементарное событие. Базис.

4. Определение вероятности. Сложение и умножение вероятностей.

5. Решение задач на основе непосредственного подсчета вероятностей (разложение по базису равновероятных событий).

6. Формула полной вероятности и формула Байеса.

Типовые задачи по математике (комплекты мир33, мир22, мир11).

5. Теория множеств.

   1. ; Заданы множества A={1,2,3,4,5,6} B={3,4,5,6,7,8}. Найти объединение, пересечение, разности этих множеств

   2. ; Определить результаты операций , если

   3. . Пусть А – множество натуральных чисел, кратных 2; В – множество натуральных чисел кратных 3. Найти АВ, АВ, А\В, В\А.

   4. Пусть А – множество точек круга единичного радиуса с центром в начале координат; В – множество всех точек координатной плоскости. Изобразить множества АВ, АВ, А\В, В\А

   5. Пусть А – множество различных букв слова «множество»; В – множество различных букв слова «содружество». Найти АВ, АВ, А\В, В\А.

   6. Пусть А – множество различных букв слова «РЕКЛАМА», В – множество различных букв слова «МАРКЕТИНГ». Найти АВ, АВ, А\В, В\А.

   7. Пусть А = { (x, y) | x<y}; В = {(x, y) | y >0 } Изобразить множества АÇВ, ВÈА, А\В, В\А.

   8. Даны множества A = {1,5,7,137}, B = {5,7,23}, C = {0,1,5, 23}, D = {0,7,23,1998}. Найдите множество (AB) \ (CD)

   9. Пусть А={Аня; Лена; Вова}, B={Велосипед; Ролики}. Найти декартово произведение AxB. Выделить из него функцию

6. Математическая логика.

   1. Пусть a - высказывание «Студент Иванов изучает английский язык», b - высказывание «Студент Иванов успевает по математической логике». Дать словесную формулировку высказываний: 1) ; 2) ; 3)

   2. Составить таблицу истинности для формулы

   3. Доказать равносильность .

   4. . Упростить формулу .

   5. . Даны предикаты : и 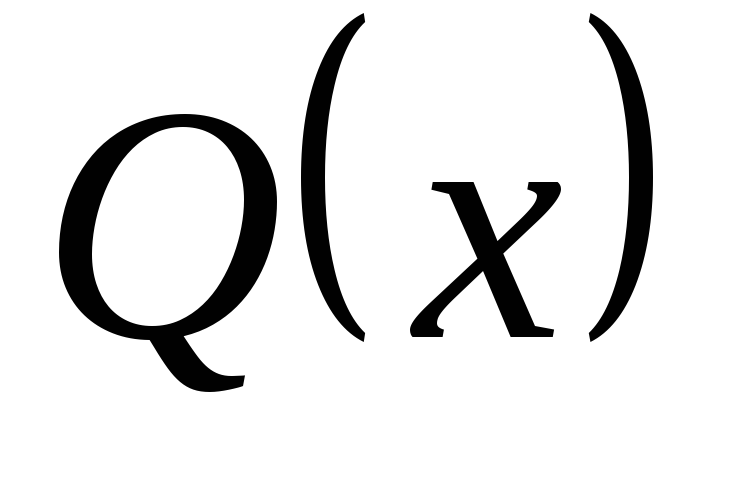: , определенные на множестве R. Требуется установить, какие из следующих высказываний истинны и какие ложны: 1) 2) 3) 4) .

   6. Пусть даны предикаты: P(x): «x -четное число» и Q(x): «x кратно 3», определенные на множестве N. Найти области истинности предикатов: 1) 2) 3) 4) .

7. Комбинаторика.

   1. Вычислить

   2. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?

   3. . В группе 20 юношей и 10 девушек. Сколькими способами можно избрать трех юношей и двух девушек для участия в слете студентов

   4. Сколько прямых можно провести через 8 точек, никакие 3 из которых не лежат на одной прямой, так чтобы каждая прямая проходила через 2 точки?

   5. Сколько различных шестизначных чисел, начинающихся цифрой 2 и оканчивающихся цифрой 5, можно составить из цифр 1, 2, 3, 4, 5, 6 при условии, что каждая цифра в обозначении числа встречается 1 раз?

   6. Найти m и n, если .

   7. Вычислить: .

8. Теория вероятностей.

   1. Вероятность того, что день будет ясным p = 0.85. Найти вероятность q того, что день будет облачным

   2. Ребенок берет карточки в случайном порядке и прикладывает все 6 карточек одну к другой. Найти вероятность того, что получится слово «АНАНАС», если на отдельных карточках написаны три буквы А, две буквы Н и одна буква С

   3. В урне 4 белых и 7 черных шаров. Из урны одновременно вынимают два шара. Какова вероятность того, что оба шара белые?

   4. Игральная кость бросается один раз. Найти вероятность того ,что появится не менее пяти очков.

   5. В урне 4 белых и 6 черных шаров. Из урны вынимают сразу 2 шара. Найти вероятность того, что шары разного цвета.

   6. Пусть, испытание-приобретение одного лотерейного билета; событие А-«выигрыш 1000 рублей»; событие В-«отсутствие выигрыша». Найти A+B и A·B. Как называются полученные события? Чему равны их вероятности? Объяснить полученные результаты.

   7. Фирма изготовила две партии компьютеров. Первая партия компьютеров в два раза больше второй. Надежность компьютеров первой партии-0.98, второй партии-0.94. Определить вероятность того, что наугад купленный компьютер будет надежным.