лабораторная работа / lab_2 / лаб тау 2

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

Кафедра АПУ

Отчет

по лабораторной работе №2

по дисциплине «Теория автоматического управления»

на тему «Анализ временных и частотных характеристик дискретных звеньев»

Выполнили: Баландин Евгений и Гагарин Глеб, гр 4322.

Проверил: Имаев Д. Х..

2007 г.

Пример 1.

Дискретный интегратор.

Разностное уравнение дискретного интегратора:

Для того чтобы получить дискретную передаточную функцию (ДПФ) применим

Z – преобразование к разностному уравнению:

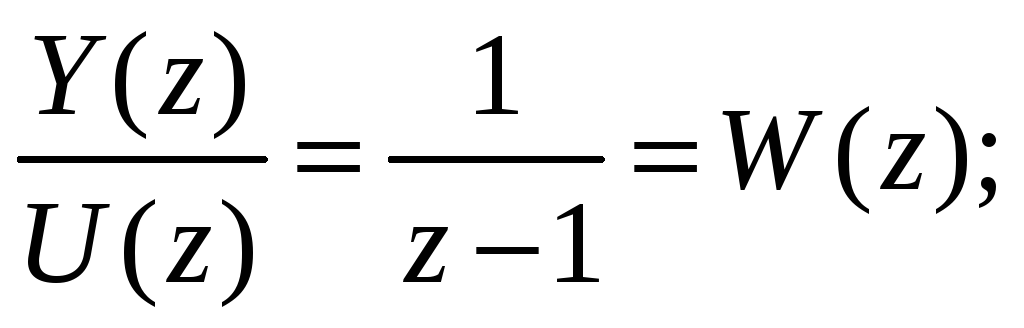
Временные характеристики – реакции на типовые воздействия при нулевых начальных условиях.

Одним из таких типовых воздействий является единичная ступенчатая последовательность. Реакция на нее называется переходной последовательностью.

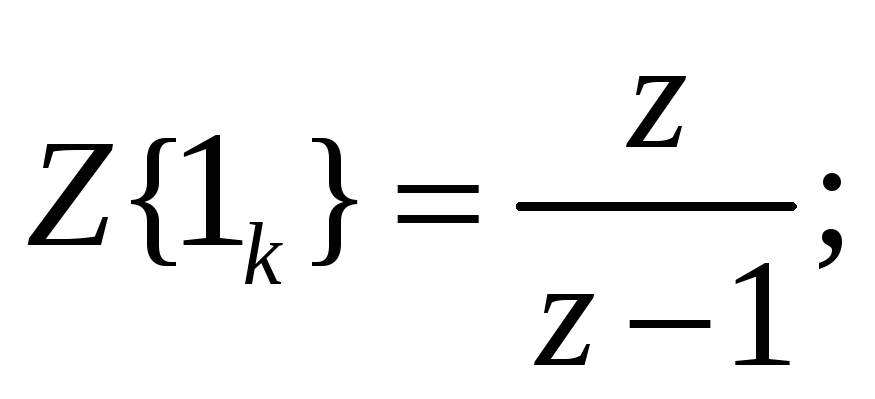
Реакция представляет собой:

Для построения временной характеристики воспользуемся специальной командой Matlab/Control System Toolbox (Рис. 2.1):

dstep (1,[1 -1]);

Рис 2.1. Переходная последовательность дискретного интегратора.

Для построения частотных характеристик по ДПФ необходимо заменить аргумент z:

При этом аргумент проходит дугу от 0 до по окружности единичного радиуса с центром в начале координат.

Получаемая при этом характеристика называется амплитудно-фазовой.

Но проще всего ее получить, используя специальную команду Matlab/Control System Toolbox (Рис. 2.2):

dnyquist (1,[1 -1],1);

Рис 2.2. Амплитудно-фазовая характеристика дискретного интегратора.

Дискретный интегратор, в отличие от непрерывного, вносит фазовый сдвиг от до.

Для построения частотных характеристик будем использовать команду

dbode (1,[1 -1],1);

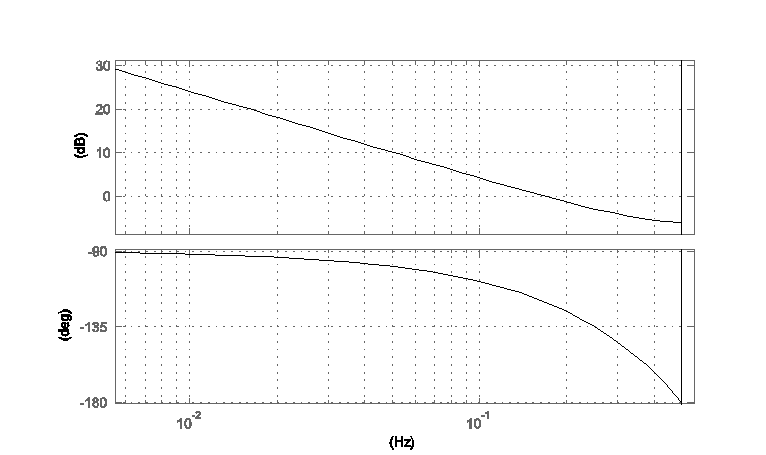
Результат выполнения этой команды показан на рисунке 2.3.

Рис 2.3. Амплитудно-фазовая характеристика дискретного интегратора.

Пример 2.

Дискретное звено 1-го порядка.

Разностное уравнение дискретного звена 1-го порядка:

Дискретная передаточная функция этого звена может быть найдена с использованием Z-преобразования:

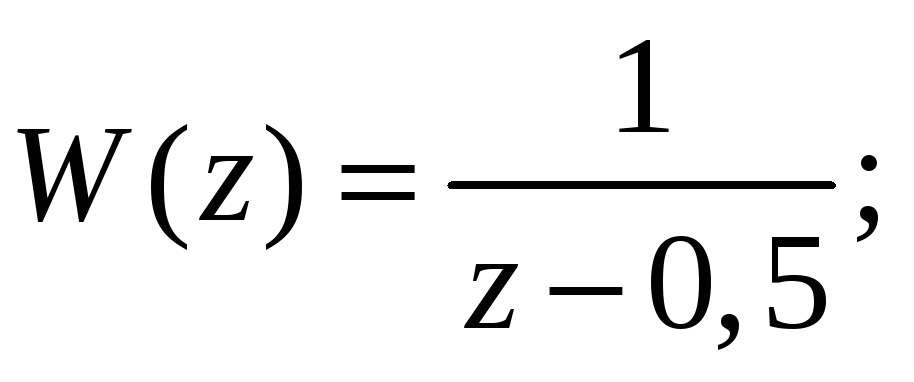
Найдем переходную последовательность

Для построения временной характеристики воспользуемся специальной командой Matlab/Control System Toolbox (Рис. 2.4):

dstep (1,[1 -0.5]);

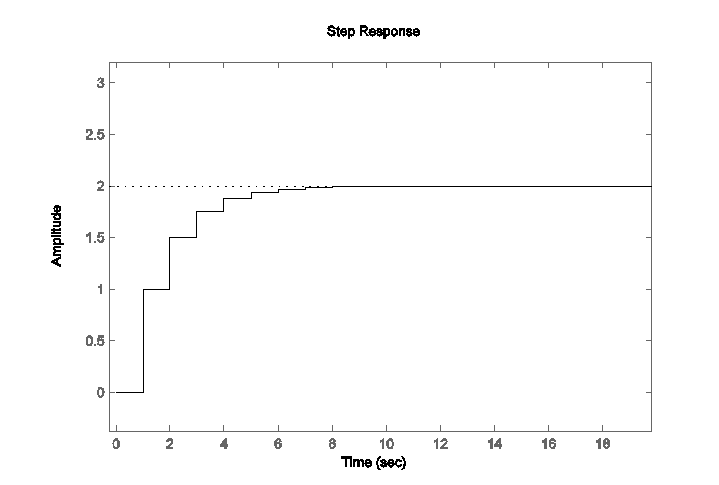
Рис 2.4. Переходная последовательность дискретного звена 1-го порядка.

Частотные характеристики, полученные с помощью команд Matlab

dbode (1,[1 -0.5],1);

dnyquist (1,[1 -0.5],1);

показаны на рис. 2.5 и 2.6 соответственно

Рис 2.5. АЧХ и ФЧХ дискретного звена 1-го порядка.

Рис 2.6. Амплитудно-фазовая характеристика дискретного звена 1-го порядка.

Пример 3.

Дискретное звено 2-го порядка.

Разностное уравнение дискретного звена 1-го порядка:

Дискретная передаточная функция этого звена может быть найдена с использованием Z-преобразования:

Для того, чтобы узнать расположение корней ХП, воспользуемся командой (Рис 2.7):

pzmap([1],[1 -1 -1]);

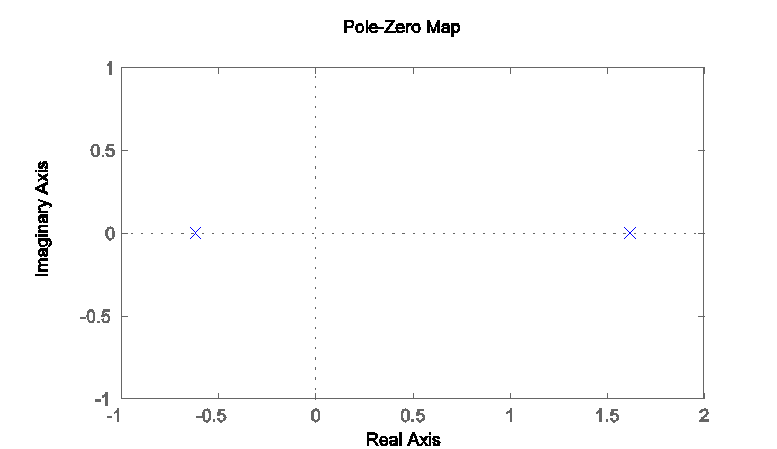
Рис 2.7. .Расположение корней ХП на комплексной плоскости.

Из рисунка видно, что один из корней лежит за пределами единичной окружности. Это говорит о неустойчивости звена.

Построим переходную характеристику с помощью команды:

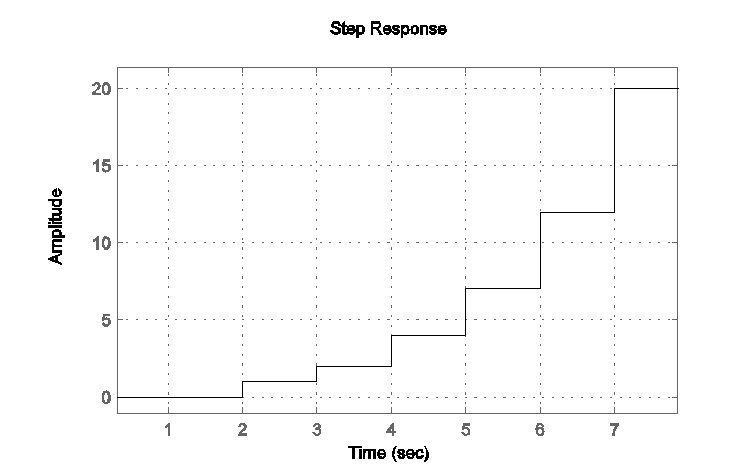dstep([1],[1 -1 -1]);

Рис 2.8. Переходная последовательность дискретного звена 2-го порядка.

Переходная характеристика подтверждает факт неустойчивости звена.

Частотные характеристики, полученные с помощью команд Matlab рисунок 2.9 и 2.10

dbode (1,[1 -1 -1],1);

dnyquist (1,[1 -1 -1],1);

Рис 2.9. АЧХ и ФЧХ дискретного звена 1-го порядка.

Рис 2.10. Амплитудно-фазовая характеристика дискретного звена 2-го порядка.