4.3. Движение заряженной частицы в однородном постоянном магнитном поле.

В данном случае и сила Лоренца имеет только магнитную составляющую . Уравнением движения частицы, записанном в декартовой системе координат, в этом случае является:

.

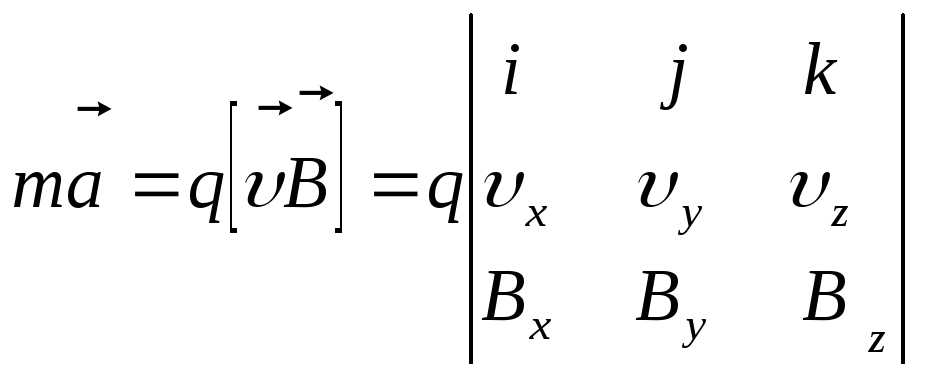Рассмотрим сначала случай, когда частица влетает под прямым углом к силовым линиям магнитного поля (рис.13.3).

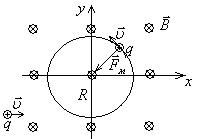
Рис.13.3. Движение заряженной частицы в магнитном поле ().

В системе координат, показанной на рис.13.3, , , и уравнение движения принимает вид:

,

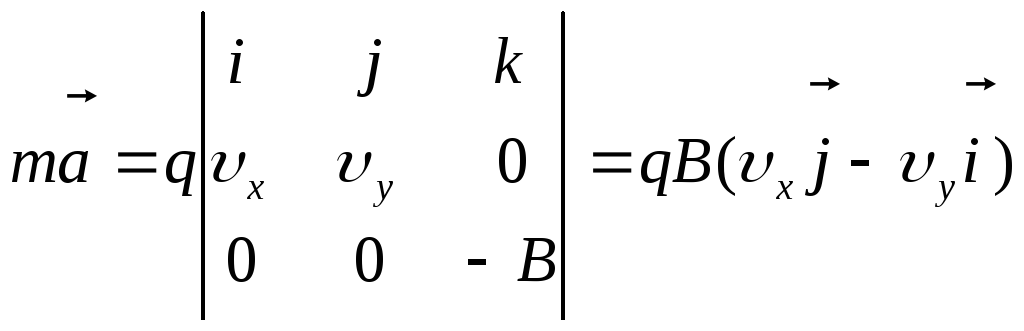откуда следует, что вектор полного ускорения частицы лежит в плоскости, перпендикулярной вектору . Легко убедиться также в том, что вектор ускорения перпендикулярен вектору скорости частицы и составляет вместе с вектором правую тройку векторов (как и должно быть по свойствам силы Лоренца). Действительно,

.

Таким образом, ускорение частицы в каждый момент времени t направлено к центру кривизны траектории и играет роль нормального (центростремительного) ускорения. Модуль ускорения равен:

.

Траекторией движения является окружность, радиус R которой находим из условия: , то есть , откуда:

.

Период обращения частицы

Отметим, что период обращения и соответственно угловая скорость движения частицы не зависят от линейной скорости .

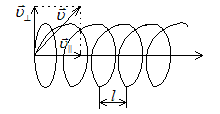
Рассмотрим теперь случай, когда частица влетает под углом α к силовым линиям магнитного поля (рис.13.4).

Рис.13.4. Общий случай движения заряженной частицы в однородном магнитном поле.

Разложим вектор скорости на две составляющие: - параллельную вектору и - перпендикулярную . Поскольку составляющая силы Лоренца в направлении равна нулю, она не может повлиять на величину . Что касается составляющей , то этот случай был рассмотрен выше. Таким образом, движение частицы можно представить как наложение двух движений: одного – равномерного перемещения вдоль направления силовых линий поля со скоростью , второго – равномерного вращения в плоскости, перпендикулярной . В итоге траекторией движения будет винтовая линия (рис.13.4).

Шаг винтовой линии определяется по формуле:

, где .

Радиус витка находим по формуле:

Направление, в котором закручивается винтовая линия, зависит от знака заряда частицы. Если заряд частицы положительный, то винтовая линия закручивается против часовой стрелки, если смотреть вдоль направления , и наоборот – по часовой стрелке, если заряд частицы отрицательный.

4.4. Практические применения силы Лоренца. Эффект Холла.

К числу одного из известных проявлений силы Лоренца относится эффект, обнаруженный Холлом (Hall E., 1855-1938) в 1880г.

Рис.13.5. К объяснению эффекта Холла.

Суть явления заключается в следующем: если металлическую пластинку, вдоль которой течет постоянный ток, поместить в магнитное поле (рис.13.5), то между параллельными току и полю гранями пластинки возникает разность потенциалов, величина которой определяется выражением:

,

где b – толщина пластинки; j - плотность тока; R – так называемая постоянная Холла.

Эффект Холла объясняется действием силы Лоренца на движущиеся в металле электроны, создающие ток. Направление тока противоположно направлению движения электронов. Поэтому при включении магнитного поля на каждый электрон будет действовать сила, направленная к нижней грани пластинки и равная по величине

.

В результате на нижней грани появятся избыточные отрицательные заряды, а на верхней - соответственно избыточные положительные заряды. Между верхней и нижней гранью возникнет разность потенциалов U, то есть электрическое поле. Напряженность поля . Сила, действующая на электрон со стороны этого поля, направлена вверх и равна по величине:

.

При установившемся процессе разделения зарядов , откуда, принимая во внимание, что плотность тока , находим холловскую разность потенциалов:

Постоянная Холла , где n – концентрация электронов в металле.

Эффект Холла наблюдается не только в металлах, но и в полупроводниках, а также в электролитах. Знак холловской разности потенциалов зависит от знака носителя заряда. Поэтому эффект Холла широко применяют не только для определения концентрации носителей заряда в полупроводниках, но также для определения типа полупроводника.

Из других практических применений силы Лоренца отметим использование ее в различных электронных устройствах (кинескоп, магнетрон), масс-спектрографах, ускорителях заряженных частиц, других устройствах и приборах.