Лекция 13

4. Основы электродинамики Движение заряженных частиц в постоянных электрическом и магнитном полях.

4.1. Силы, действующие на заряженную частицу в электромагнитном поле. Сила Лоренца.

Мы уже знаем, что на проводник с током, помещенный в магнитное поле, действует сила Ампера. Но ток в проводнике – есть направленное движение зарядов. Отсюда напрашивается вывод, что сила, действующая на проводник с током в магнитном поле, обусловлена действием сил на отдельные движущиеся заряды, от которых это действие передается уже самому проводнику. Этот вывод подтверждается, в частности, еще и тем, что пучок свободно летящих заряженных частиц отклоняется магнитным полем.

Сила Ампера, действующая на элемент тока в магнитном поле с индукцией :

,

где α – угол между направлением тока в проводнике и вектором.

Пусть – скорость упорядоченного движения зарядов в проводнике; q – заряд носителя тока (в металлах q = - e). Для элемента тока можем написать:

dNq,

где n = dN/dV – концентрация зарядов, dN – число зарядов в элементе объема dV = Sdl.

Тогда, сила, действующая в магнитном поле на один заряд, будет:

или в векторном виде

.

Эту силу называют силой Лоренца (Lorentz H., 1853-1928).

Свойства силы Лоренца:

1. сила Лоренца действует только на движущуюся заряженную частицу;

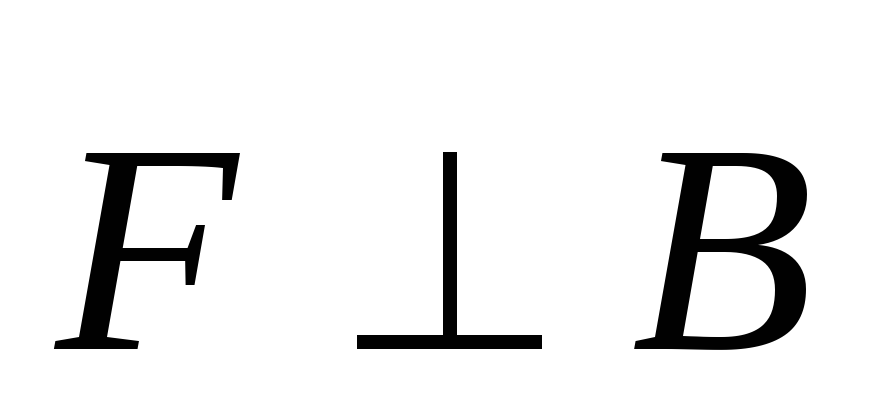2. и одновременно ;

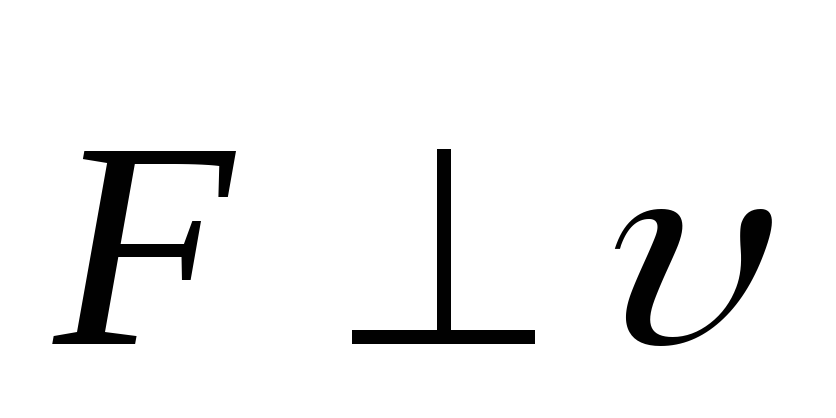3. поскольку 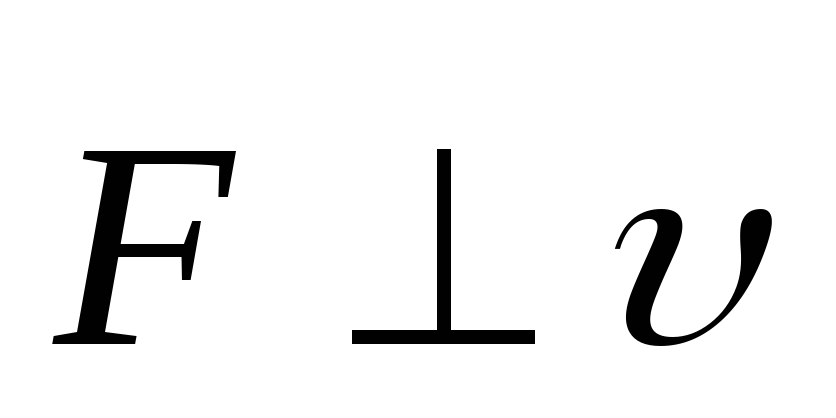, то сила Лоренца не совершает работу, а следовательно, не может изменить энергию частицы.

Если помимо магнитного поля присутствует еще и электрическое поле , то на частицу действует дополнительная сила:

Полная сила, действующая на заряженную частицу в электромагнитном поле (которую также называют силой Лоренца) есть:

4.2. Движение заряженной частицы в однородном постоянном электрическом поле.

В данном случае и сила Лоренца имеет только электрическую составляющую . Уравнением движения частицы в этом случае является:

.

Рассмотрим две ситуации: а) и б) .

а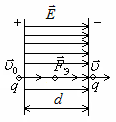) (рис.13.1).

Рис.13.1. Движение заряженной частицы в электрическом поле ().

Изменение кинетической энергии частицы на пути d происходит за счет работы силы :

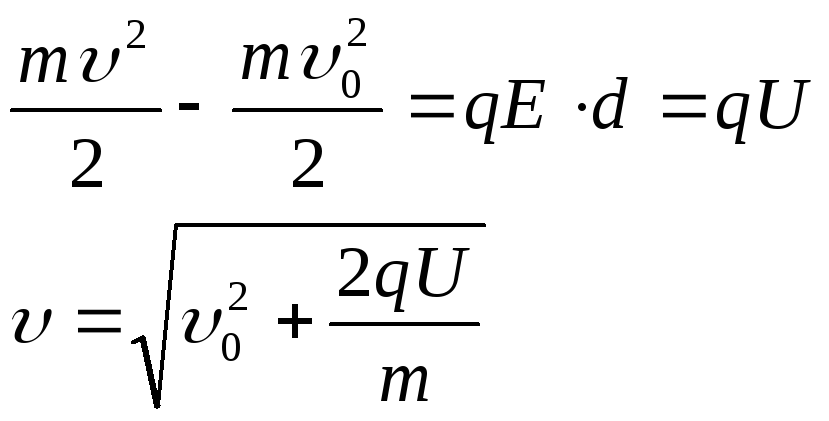, откуда

где - ускоряющее напряжение.

В частности, если начальная скорость частицы , то

.

Время пролета частицы в электрическом поле и пройденный путь находим из уравнений:

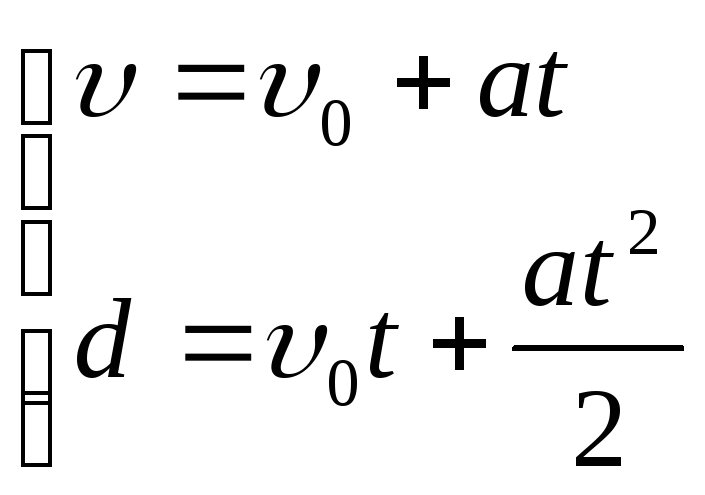
б) (рис.13.2).

Рис.13.2. Движение заряженной частицы в электрическом поле ().

В данном случае проекции уравнения движения частицы на координатные оси дают:

.

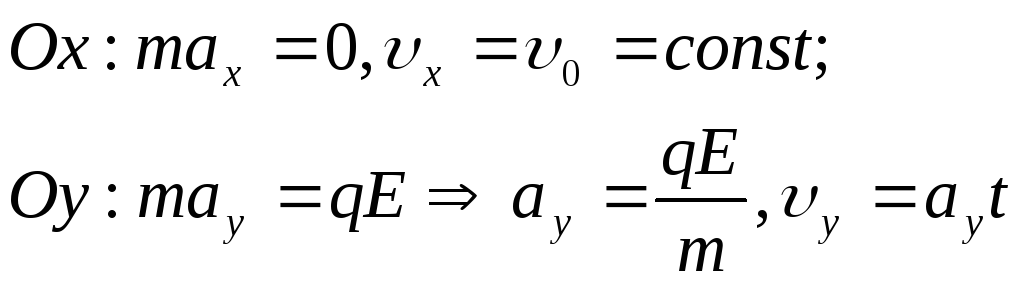Координаты частицы в момент времени t составляют:

; .

Исключая из этих уравнений параметр t , находим уравнение траектории частицы:

Видим, что траекторией движения частицы является парабола.

Определим смещение следа частицы на экране, отстоящем от конденсатора на расстоянии b (рис.13.2):

,

где - смещение частицы по вертикали, полученное ею в электрическом поле к моменту вылета из конденсатора ; - смещение частицы после вылета из конденсатора.

Таким образом, имеем:

.