3.20. Элементы теории ферромагнетизма. Представление об обменных силах и доменной структуре ферромагнетиков. Закон Кюри - Вейсса.

Как уже отмечалось ранее (Лекция 11), ферромагнетики характеризуются высокой степенью намагничивания и нелинейной зависимостью от . Основная кривая намагничивания ферромагнетика (магнитный момент которого первоначально был равен нулю) показана на рис.12.2. При достижении насыщения В продолжает расти по линейному закону:

.

Кроме нелинейной зависимости В(Н), для ферромагнетиков характерно явление гистерезиса – запаздывание намагниченности за изменением магнитного поля. Если довести намагничивание до насыщения, а затем уменьшать напряженность внешнего магнитного поля, то индукция поля будет следовать не по первоначальной (основной) кривой намагничивания, а пойдет несколько выше. В результате, когда напряженность магнитного поля станет равной нулю, индукция поля не исчезнет и будет характеризоваться величиной B_r , называемой остаточной индукцией.

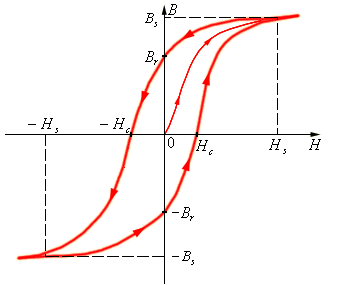
Рис.12.2. Основная кривая намагничивания и петля гистерезиса ферромагнетика.

Существование остаточной намагниченности делает возможным изготовление постоянных магнитов, то есть тел, обладающих макроскопическим магнитным моментом, на поддержание которого не требуются затраты энергии.

Намагниченность ферромагнетика обращается в нуль лишь под действием магнитного поля Н_с , имеющего направление, противоположное намагничивающему полю (рис.12.2). Напряженность поля Н_с называют коэрцитивной силой. Если коэрцитивная сила велика, ферромагнетик называют жестким; для такого ферромагнетика характерна широкая петля гистерезиса. Ферромагнетик с малой коэрцитивной силой (и соответственно узкой петлей гистерезиса) называют мягким.

Петля гистерезиса образуется при циклическом перемагничивании ферромагнетика. В зависимости от значения намагничивающего поля Н, различают частный цикл и максимальную петлю гистерезиса. Отсюда следует, что намагниченность ферромагнетика в сильной мере зависит от предшествующей истории его пребывания в магнитном поле.

Магнитная восприимчивость χ, а следовательно и магнитная проницаемость μ, ферромагнетика являются функциями напряженности магнитного поля (рис.12.3). Для некоторых ферромагнетиков величина μ_max может достигать значений ~800 000 (супермаллой).

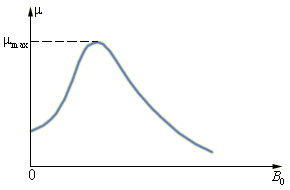
Рис.12.3. Кривая зависимости μ(Н) для ферромагнетика.

Теория ферромагнетизма была создана Я.И. Френкелем (1894-1952) и В.Гейзенбергом (Heisenberg W., 1901-1976) в 1928г. Согласно этой теории, ответственными за магнитные свойства ферромагнетиков являются собственные (спиновые) магнитные моменты электронов. При определенных условиях между электронами возникают так называемые обменные силы, имеющие особую электростатическую (не магнитную) природу. Благодаря действию этих сил магнитные моменты электронов выстраиваются параллельно друг другу. В результате возникают области спонтанного (самопроизвольного) намагничения ферромагнетика, которые называются доменами. В пределах каждого домена ферромагнетик намагничен до насыщения и обладает определенным магнитным моментом. Для разных доменов эти моменты имеют различное направление, так что в отсутствие внешнего магнитного поля суммарный магнитный момент всего тела равен нулю.

При намагничивании ферромагнетика сначала происходит смещение границ доменов, в результате чего домены, магнитный момент которых составляет с направлением внешнего магнитного поля наименьший угол, увеличиваются за счет уменьшения других доменов (рис.12.4). Этот процесс идет до тех пор, пока весь объем ферромагнетика не станет монодоменным.

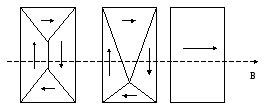
Рис.12.4. Смещение границ доменов при намагничивании ферромагнетика.

На следующей стадии имеет место поворот магнитного момента домена в направлении поля. При этом магнитные моменты электронов в пределах домена поворачиваются одновременно. Эти процессы являются необратимыми, что и служит причиной появления гистерезиса.

Каждый ферромагнетик характеризуется температурой Т_C , называемой точкой Кюри, выше которой области спонтанной намагниченности распадаются и ферромагнетик утрачивает свои свойства. В таблице приведены значения Т_C для железа, никеля и кобальта – трех чистых металлов ферромагнетиков.

Таблица. Точка Кюри.

Fe	768°C
Ni	365oC
Co	1150oС

При температуре выше точки Кюри ферромагнетик становится обычным парамагнетиком, магнитная восприимчивость которого подчиняется закону Кюри-Вейсса:

, T > T_C .

При охлаждении ферромагнетика ниже точки Кюри в нем снова возникают домены, и ферромагнетик вновь приобретает свои первоначальные свойства.