3.18. Природа диамагнетизма. Теорема Лармора.

Если атом поместить во внешнее магнитное поле с индукцией (рис.12.1), то на электрон, движущийся по орбите, будет действовать вращательный момент сил , стремящийся установить магнитный момент электрона по направлению силовых линий магнитного поля (механического момента - против поля).

Рис.12.1. К объяснению природы диамагнетизма.

Под действием момента силвекторы и совершают прецессионное движение вокруг направления вектора магнитной индукции с угловой скоростью ω_L, которую легко найти.

Как следует из рис.12.1, . За время dt плоскость, в которой лежит вектор ,повернется вокруг направления на угол

,

откуда находим:

Или, с учетом значения гиромагнитного отношения Γ для орбитального движения электрона,

.

Частоту ω_L называют частотой ларморовой прецессии. Она не зависит от угла наклона орбиты α, радиуса орбиты r и скорости движения электрона по орбите – теорема Лармора (Larmor J., 1857-1942).

Прецессия орбиты обусловливает дополнительное движение электрона вокруг направления поля. Этому движению соответствует круговой ток I^′ = eν_L = eω_L /(2π), магнитный момент которого

,

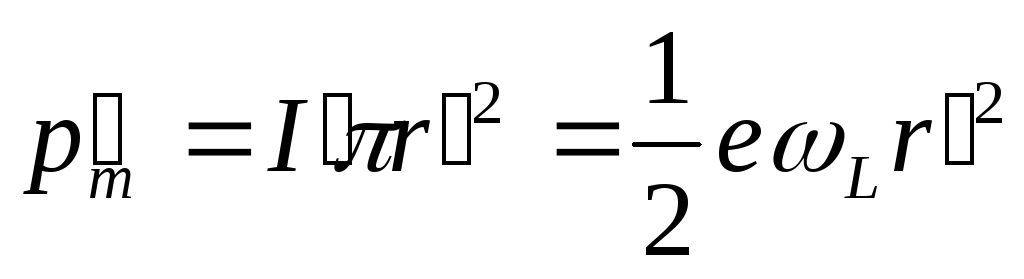где r^′ - радиус штриховой окружности на рис.12.1.

Наведенный (индуцированный) магнитный момент , как это видно из рис.12.1, направлен в сторону, противоположную . Строгий анализ показывает, что в действительности, в атомах со многими электронными орбитами, ориентированными всевозможными способами, в последней формуле надо брать вместо r^{′ 2} среднее значение < r^{′ 2} > = 2r²/3. Тогда, с учетом знака направления вектора, получим для среднего магнитного момента электрона:

Просуммировав это выражение по всем электронам в атоме, найдем индуцированный магнитный момент атома в целом, а умножив полученный результат на μ₀N_A – магнитную восприимчивость одного моля вещества:

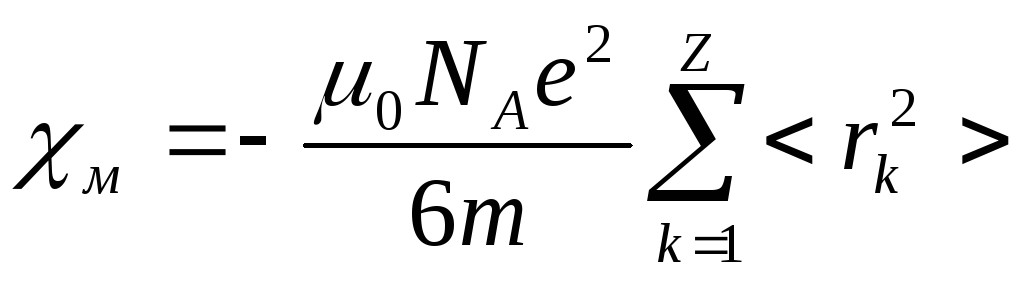
где Z – число электронов в атоме, равное его атомному номеру; N_A =6,02∙10²³ моль^-1 – число Авогадро.

Оценки χ_м по этой формуле дают величину, хорошо согласующуюся с экспериментальными данными.

Итак, под действием внешнего магнитного поля происходит прецессия электронных орбит с одинаковой для всех электронов угловой скоростью ω_L. Обусловленное этой прецессией дополнительное движение электронов приводит к возникновению индуцированного магнитного момента атома, направленного против поля, то есть – к диамагнетизму. Заметим, что диамагнетизм присущ всем без исключения веществам, но обнаруживается он лишь у тех веществ, атомы которых не обладают собственным магнитным моментам. В противном случае результирующий магнитный момент атома оказывается положительным и вещество ведет себя уже как парамагнетик.

3.19. Парамагнетизм. Закон Кюри. Теория Ланжевена.

Если магнитный момент атомов отличен от нуля, то вещество оказывается парамагнитным. Внешнее магнитное поле стремится установить магнитные моменты атомов вдоль в то время, как тепловое движение – разбросать их равномерно по всем направлениям. В результате устанавливается некоторая преимущественная ориентация магнитных моментов атомов вдоль поля. Пьер Кюри (Curie P., 1859-1906) экспериментально установил, что магнитная восприимчивость парамагнетика зависит от температуры согласно закону (закон Кюри):

,

где С – постоянная Кюри, зависящая от рода вещества.

Количественная теория парамагнетизма была разработана Полем Ланжевеном (Langevin P., 1872-1946) в 1905г. В упрощенном варианте (не слишком сильных магнитных полей и не слишком низких температур) суть теории Ланжевена сводится к следующему. В магнитном поле атом обладает потенциальной энергией W = - p_mBcosθ, которая зависит от угла θ между векторами и . Число атомов в единице объема, магнитные моменты которых направлены в пределах телесного угла dΩ=2πsinθdθ, определяется законом распределения Больцмана:

,

где А – нормирующий множитель, определяемый из условия

Эти атомы вносят вклад в проекцию вектора намагничивания на направление внешнего магнитного поля:

,

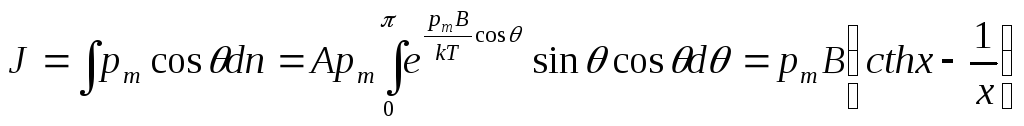где обозначено .

В принятом выше приближении x<<1 можно ограничиться первыми двумя членами в разложении Тогда получим:

,

откуда следует выражение для магнитной восприимчивости парамагнетика:

.

Полученное выражение совпадает с законом Кюри, причем для постоянной Кюри С имеем: .