1.2. Взаимодействие электрических зарядов. Закон Кулона. Применение закона Кулона для расчета сил взаимодействия протяженных заряженных тел.

Закон взаимодействия электрических зарядов был установлен в 1785 г. Шарлем Кулоном (Coulomb Sh., 1736-1806). Кулон измерял силу взаимодействия двух небольших заряженных шариков в зависимости от величины зарядов и расстояния между ними с помощью специально сконструированных им крутильных весов (рис.1.3). В результате своих опытов Кулон установил, что сила взаимодействия двух точечных зарядов прямо пропорциональна величине каждого из зарядов и обратно пропорциональна квадрату расстояния между ними, при этом направление действия силы совпадает с прямой, проходящей через оба заряда:

~ , ~ , ||.

Другими словами, можем написать:

Коэффициент пропорциональности k зависит от выбора

единиц измерения входящих в эту формулу величин:

Рис.1.3. Крутильные весы Кулона (схема).

В общепринятой сейчас Международной системе единиц измерения (СИ) закон Кулона записывается, следовательно, в виде:

Необходимо еще раз подчеркнуть, что в таком виде закон Кулона формулируется только для точечных зарядов, то есть таких заряженных тел, размерами которых можно пренебречь по сравнению с расстоянием между ними. Если это условие не выполняется, то закон Кулона должен быть записан в дифференциальной форме для каждой пары элементарных зарядов dq₁ и dq₂, на которые «разбиваются» заряженные тела:

.

Тогда полная сила взаимодействия двух макроскопических заряженных тел будет представлена в виде:

Интегрирование в этой формуле производится по всем зарядам каждого тела.

Пример. Найти силу F, действующую на точечный заряд Q со стороны бесконечно протяженной прямолинейной заряженной нити (рис.1.4). Расстояние от заряда до нити a, линейная плотность заряда нити τ.

Рис.1.4. К расчету силы F.

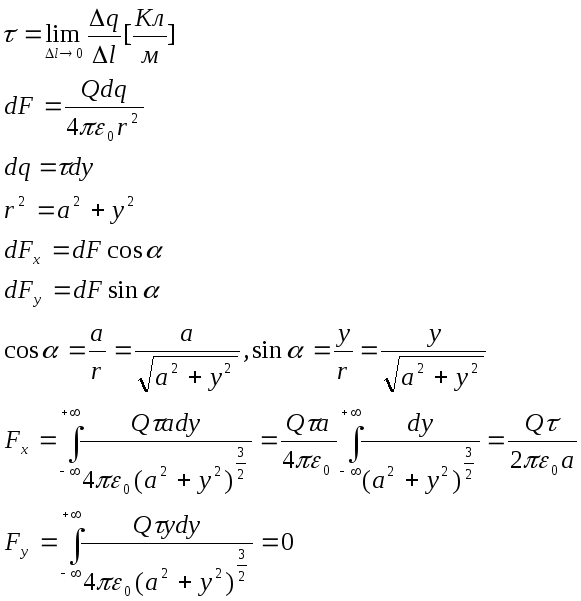
Искомая сила F = F_x= Qτ/(2πε₀a).

1.3. Электрическое поле. Напряженность электрического поля. Принцип суперпозиции электрических полей.

Взаимодействие электрических зарядов осуществляется через особый вид материи, порождаемой заряженными частицами - электрическое поле. Электрические заряды изменяют свойства окружающего их пространства. Проявляется это в том, что на помещенный вблизи заряженного тела другой заряд (назовем его пробным) действует сила (рис.1.5). По величине этой силы можно судить об «интенсивности» поля, созданного зарядом q. Для того, чтобы сила, действующая на пробный заряд, характеризовала электрическое поле именно в данной точке пространства, пробный заряд, очевидно, должен быть точечным.

Рис.1.5. К определению напряженности электрического поля.

Поместив пробный заряд q_пр на некотором расстоянии r от заряда q (рис.1.5), мы обнаружим, что на него действует сила, величина которой

зависит от величины взятого пробного заряда q_пр. Легко, однако, видеть, что для всех пробных зарядов отношение F/ q_пр будет одно и тоже и зависит лишь от величин q и r , определяющих поле заряда q в данной точке r. Естественно, поэтому, принять это отношение за величину, характеризующую «интенсивность» или, как говорят, напряженность электрического поля (в данном случае поля точечного заряда):

.

Таким образом, напряженность электрического поля является его силовой характеристикой. Численно она равна силе, действующий на пробный заряд q_пр = +1, помещенный в данное поле.

Напряженность поля – вектор. Его направление совпадает с направлением вектора силы, действующей на точечный заряд, помещенный в это поле. Следовательно, если в электрическое поле напряженностью поместить точечный заряд q, то на него будет действовать сила:

Размерность напряженности электрического поля в СИ: .

Электрическое поле удобно изображать с помощью силовых линий. Силовая линия – линия, вектор касательной к которой в каждой точке совпадает с направлением вектора напряженности электрического поля в этой точке. Принято считать, что силовые линии начинаются на положительных зарядах и оканчиваются на отрицательных (или уходят на бесконечность) и нигде не прерываются. Примеры силовых линий некоторых электрических полей приведены на рис.1.6.

Рис.1.6. Примеры изображения электрических полей с помощью силовых линий: точечного заряда (положительного и отрицательного), диполя, однородного электрического поля.

Электрическое поле подчиняется принципу суперпозиции (сложения), который можно сформулировать следующим образом: напряженность электрического поля, созданного в некоторой точке пространства системой зарядов, равна векторной сумме напряженностей электрических полей, созданных в этой же точке пространства каждым из зарядов в отдельности:

Пример. Найти напряженность электрического поля Е диполя (системы двух жестко связанных точечных зарядов противоположного знака) в точке, находящейся на расстоянии r₁ от заряда - q и на расстоянии r₂ от заряда +q (рис.1.7). Расстояние между зарядами (плечо диполя) равно l.

Рис.1.7. К расчету напряженности электрического поля системы двух точечных зарядов.

, где

, .

Угол α определяется по теореме косинусов: .