лабораторная работа / Практическая работа 1 - 41

Дано:

структурная схема системы управления (СУ)

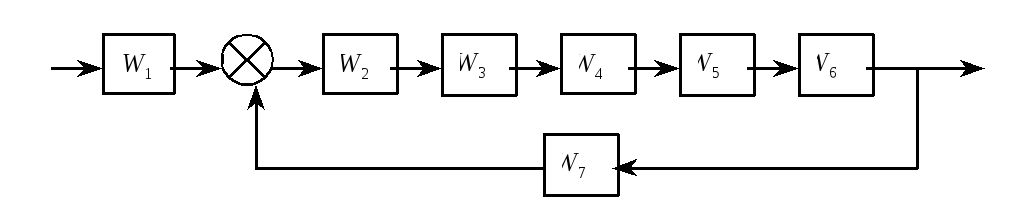
Провести анализ устойчивости СУ методами:

1. Ляпунова

2. Рауса

3. Гурвица

4. Льенера-Шипара

5. Михайлова

6. Найквиста

7. D-разбиения

8. Шур-Кона

Передаточная функция разомкнутой системы:

Передаточная функция замкнутой системы:

Система является устойчивой по критерию Ляпунова, если все корни характеристического уравнения лежат в левой полуплоскости.

Характеристическое уравнение замкнутой системы:

Уравнение имеет 1 действительный отрицательный корень и 2 комплексно-сопряженных корня, лежащих в правой полуплоскости, следовательно замкнутая система неустойчива.

Определим устойчивость системы по методу Рауса.

Составим программу для построения таблицы Рауса:

Коэффициенты характеристического уравнения:

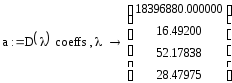
Поскольку один из коэффициентов 1 столбца таблицы отрицателен, система неустойчива.

Определим устойчивость системы по методу Гурвица.

Составим программу для построения определителей Гурвица:

Вычислим определители:

Не все определители Гурвица положительны, следовательно система неустойчива.

Критерий Льенера-Шипара состоит в следующем: если выполняется необходимое условие устойчивости (все коэффициенты характеристического уравнения положительны), достаточно вычислить только четные (нечетные) определители Гурвица; если все они положительны, система устойчива.

Поскольку один нечетный определитель Гурвица меньше 0, система неустойчива.

Определим устойчивость СУ по критерию Михайлова.

Заменим в характеристическом уравнении p на j и выделим действительную и мнимую части:

Построим годограф Михайлова:

Система устойчива по критерию Михайлова, если годограф Михайлова, начинаясь на положительной вещественной полуоси, при изменении частоты от нуля до бесконечности повернулась в положительном направлении вокруг начала координат последовательно, нигде не обращаясь в ноль на n квадрантов, где n - порядок характеристического уравнения.

Как видно из графика, кривая Михайлова началась на вещественной положительной полуоси, но нарушила порядок прохождения квадрантов (4,3 вместо 1,2,3), следовательно система неустойчива.

Определим устойчивость замкнутой САУ по АФЧХ разомкнутой методом Найквиста.

Определим устойчивость разомкнутой системы методом Ляпунова:

Так как оба корня отрицательные, система устойчива.

Найдем АФЧХ разомкнутой системы:

Построим годограф Найквиста (АФЧХ разомкнутой системы):

Чтобы САУ, устойчивая в разомкнутом состоянии, была устойчива в замкнутом, необходимо и достаточно, чтобы кривая АФЧХ разомкнутой системы при изменении частоты от нуля до бесконечности не охватывала точку (-1 + j0).

Как видно из графика, годограф Найквиста не охватывает точку (-1 + j0), следовательно система будет устойчива в замкнутом состоянии.

Определим область устойчивости системы методом D-разбиения.

D-разбиение - разбиение плоскости искомого параметра на области, в которых число корней с положительной действительной частью постоянно. Область устойчивости - область с числом корней с положительной вещественной частью, равным 0. Оптимальное значение параметра выбирается на вещественной оси в середине области устойчивости. Граница D-разбиения - решение характеристического уравнения D(j) = 0 для искомого параметра при  = - ... +.

Построим D-разбиение по параметру T₇.

Передаточная функция замкнутой системы:

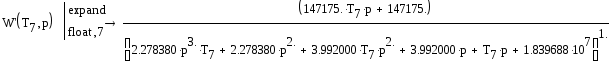
Характеристическое уравнение:

Решим его относительно искомого параметра:

Заменим p на j:

Найдем точку пересечения кривых с осью:

По правилу штриховки штрихуется левая (в направлении возрастания частоты) часть прямой.

При переходе через границу D-разбиения в сторону штриховки, число корней с положительной вещественной частью уменьшается на 1. Значение параметра выбирают на положительной вещественной полуоси в середине области устойчивости. В нашем случае область устойчивости от 10500000 до бесконечности, то есть не ограничена справа, следовательно возможно принять любое значение параметра, превышающее левую границу.

Определим устойчивость дискретной СУ методом Шур-Кона.

Для этого произведем z-преобразование передаточной функции системы.

Зададим период дискретизации:

Домножим на фиксатор нулевого порядка:

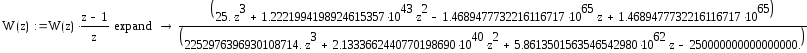
Заменим комплексную переменную z на псевдочастоту.

Составим характеристическое уравнение относительно :

Составим определители по Шур-Кону из коэффициентов уравнения.

Составим программу для построения определителей Шур-Кона:

Составим вектор коэффициентов характеристического уравнения:

Вычислим определители:

Так как знаки определителей на четных и нечетных местах не чередуются, дискретная система неустойчива.