19. Случайная величина х задана функцией плотности распределения

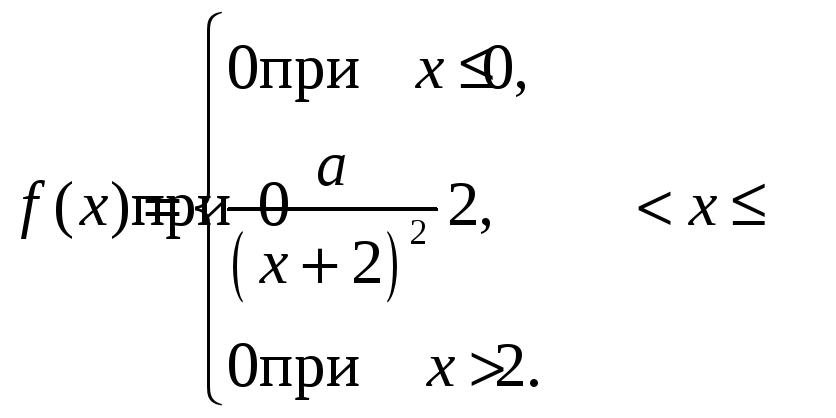
Найдите: 1) функцию распределения и необходимые константы; 2) математическое ожидание, дисперсию и среднее квадратическое отклонение; 3) вероятность попадания случайной величины Х в интервал . Постройте графики функций распределения и плотности распределения .

20. Известны математическое ожидание m и среднее квадратическое отклонение  нормально распределённой случайной величины Х. Найти вероятность попадания этой величины в заданный интервал (, ). Изобразить на графике функции плотности найденную вероятность. m=7, =2, =3, =10

21. Найти линейную среднюю квадратическую регрессию случайной величины y на случайную величину X на основе заданного закона распределения двумерной случайной величины.

Y Х	5	7	9
4	0.14	0.15	0.21
7	0.16	0.20	0.14

Вариант 8.

1. На одинаковых карточках написаны буквы А, З, К, С, У. Карточки тщательно перемешиваются и раскладываются в ряд. Какова вероятность того, что получится слово КАЗУС?

2. Из букв слова СТУДЕНТ, составленного с помощью разрезной азбуки, извлекают наудачу и складывают друг за другом в порядке их извлечения три карточки. Какова вероятность того, что получится слово НЕТ?

3. За некоторый промежуток времени амёба может погибнуть с вероятностью 0,25, выжить с вероятностью 0,25 и разделиться на две с вероятностью 0,5. В следующий такой же промежуток времени с каждой амёбой независимо от «происхождения» происходит тоже самое. Сколько амёб и с какими вероятностями может существовать к концу второго промежутка времени?

4. Из колоды в 52 карты наудачу извлекаются три карты. Каковы вероятности событий А={Извлечены три семёрки}, В={Извлечена хотя бы одна семёрка}?

5. Стрелок произвёл четыре выстрела в цель. Все элементарные исходы считать одинаково возможными. Каковы вероятности событий А={Попадание в цель при третьем выстреле}, В={Первые три выстрела попали в цель}?

6. Правильная игральная кость подбрасывается 5 раз. Каковы вероятности событий А={Последние два раза выпала шестёрка}, В={Шестёрка выпала ровно два раза}?

7. Из урны, содержащей семь белых и четыре чёрных шара, наудачу извлекают шесть шаров. Каковы вероятности событий А={Извлечён ровно два чёрных шара}, В={Извлечёно не менее трёх белых шаров}?

8. Из трёх урн, содержащих по два шара белого, чёрного, красного и синего цветов в каждой, наудачу извлекают по одному шару. Каковы вероятности событий А={Извлечён хотя бы один белый шар}, В={Извлечён ровно один чёрный шар}?

9. Три стрелка сделали по одному выстрелу в мишень. Вероятности событий А_i={Попадание в мишень i-тым стрелком}, i=1,2,3, равны 0,6. Найти вероятности событий В={В мишень попали только два стрелка}, С={В мишень попал хотя бы один стрелок}, D ={В мишень попали все}.

10. Студент пришёл на экзамен, зная 25 билетов из предложенных 100 билетов. Найти вероятность того, что он знает вытянутый билет, если он берёт билет вторым.

11. На фабрике машины a, b, c производят соответственно 30, 10, 60 процентов всех изделий. В их продукции брак составляет 3%, 2% и 18% соответственно. Найти вероятность того, что: а) случайно выбранное изделие дефектно; б) изделие произведено машиной с, если случайно выбранное изделие оказалось дефектным.

12. В каждой из двух урн по 25 белых и 8 чёрных шаров. Из первой урны во вторую переложили наудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что: а) вынутый из второй урны шар окажется чёрным; б) переложили белый шар при условии, что из второй урны вынут белый шар.

13. Слово ВОЗВРАЩЕНИЕ составлено из карточек, на каждой из которых написана одна буква. Две карточки слова потеряны. Из оставшихся карточек наугад извлекается одна карточка. Найти вероятность того, что: а) извлечена гласная буква; б) были потеряны две согласные буквы, если извлечена гласная буква.

14. На самолёте имеются шесть одинаковых двигателей. Вероятность нормальной работы каждого двигателя во время полёта равна 0,8. Какова вероятность того, что в полёте возникнут неполадки: а) в одном двигателе; б) хотя бы одном двигателе; в) хотя бы в двух двигателях; г) в пяти двигателях?

15. Аппаратура содержит 200 одинаково надёжных независимо работающих элементов, вероятность отказа для каждого из которых равна 0,005. Какова вероятность того, что при испытании аппаратуры откажет: а) три элемента; б) более пяти элементов; в) 1 или 2 элемента; г) хотя бы один элемент?

16. Известно, что вероятность прорастания семян данной партии пшеницы равна 0,95. Сколько семян следует взять из этой партии, чтобы наивероятнейшее число взошедших семян равнялось 100?

17. Испытывают 600 деталей. Вероятность того, что деталь не выдержит испытание, равна 0,55. Найдите вероятность того, что деталей, выдержавших испытание, окажется: а) 280; б) не менее 260, но не более 280.

18. Производится тестирование 5 больших интегральных схем (БИС). Вероятность того, что БИС неисправна, равна 0,6. Х – число неисправных БИС. Составьте закон распределения дискретной случайной величины Х, вычислите ее математическое ожидание, дисперсию, среднее квадратическое отклонение, а также начертите ее многоугольник распределения и график функции распределения.