
- •Алгебра высказываний
- •1. Что называется высказыванием.
- •2. Истинное и ложное высказывание.
- •3. Составные высказывания (сложные)
- •4. Логические операции над высказываниями и их определения
- •5. Основные символы, используемые в теории высказываний
- •6. Простейшие связки
- •7. Таблицы истинности высказываний и их построение
- •8. Основные законы алгебры высказываний
- •9. Булевы функции.
- •10. Построение таблицы истинности для булевых функций.
- •11. Что такое днф и кнф.
- •13. Как булевы функции связаны с формулами алгебры высказываний.
- •14. Определение многочлена Жегалкина.
- •15. Теорема Жегалкина
- •16. Алгоритм построения многочлена Жегалкина
- •I. Алгоритм
- •II. С помощью неопределённых коэффициентов
- •17. Функционально полные системы функции.
- •18. Принцип двойственности Теорем Поста и Шефферские функции.
- •Теория множеств
- •19. Понятие множ-ва, элементы множ-ва. (множ-ва - множества)
- •20. Способы задания множества.
- •22. Операции над множествами
- •23. Диаграммы Эйлера Венна
- •24. Свойства алгебры множеств
- •25. Определение Декартового произведения
- •27. Бинарные отношения на множестве
- •28. Свойства бинарных отношений
- •29. Отношение эквивалентности.
- •30. Отношение порядка
- •Предикаты
- •31. Что называется предикатами, примеры предикатов
- •32. Область истинности предикатов
- •33. Операции над предикатами
- •34. Предикатная формула
- •36. Кванторы и кванторные операции над предикатами.
- •37. Исчисление предикатов и аксиомы исчисления предикатов.
24. Свойства алгебры множеств
1) Коммутативность
A B=B
B=B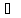 A
A
A B=B
B=B A
A
2)Ассоциативность
A (B
(B С)=(A
С)=(A B)
B) C
C
A (B
(B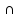 С)=(A
С)=(A B)
B) C
C
3) а)Дистрибутивность пересечения относительно объединения
A (B
(B С)=(A
С)=(A B)
B) (A
(A C)
C)
б)Дистрибутивность объединения относительно пересечения
A (B
(B С)=(A
С)=(A B)
B) (A
(A C)
C)
4)
A U=A
U=A
A Ø=A
Ø=A
5) Идемпотентность
A A=A
A=A
A A=A
A=A
6)
A (A
(A B)=A
(A
B)=A
(A B)
B) A=A
A=A
A (A
(A B)=A
(A
B)=A
(A B)
B) A=A
A=A
7)
 A=U
– Закон исключения третьего
A=U
– Закон исключения третьего
A =Ø
– Закон
противоречия
=Ø
– Закон
противоречия
8)
A U=U
U=U
A Ø= Ø
Ø= Ø
 =U
=U
 =
Ø
=
Ø
9)Законы Де Моргана
 =
=
 =
=
10)
A\B=A
11) Закон двойного отрицания
 =A
=A

25. Определение Декартового произведения
Если
X = Y, и
![]() то
говорят, что R - бинарное отношение
на множестве X. Такое отношение
называется
то
говорят, что R - бинарное отношение
на множестве X. Такое отношение
называется
-
рефлексивным, если
![]()
-
симметричным, если
![]()
-
антисимметричным, если
![]()
-
транзитивным, если
![]()
-
полным (или линейным), если
![]()
26. Степень множества и его мощность.
Степень P(a) = это множество всех подмножеств. P(a)=2n, где n – количество элементов.
Мощность m – количество элементов множества.
27. Бинарные отношения на множестве
Все пары элементов (a,b)ϵM между которыми существует отношение R образуют подмножества (бинарные) из множества всех возможных пар элементов прямого произведения MxM=M2 называемым бинарным отношением R
Область определения – DR={x|существует такое b, что aRb}
Область значений – QR={b|<a,b>ϵR}
28. Свойства бинарных отношений
А) Рефлексивность
Бинарное отношение рефлексивно если для каждого элемента aϵM данное бинарное отношение выполняется aRa – т.е. элемент а похож на себя (отношение «жить в одном городе»)
Б) Антирефлексивность
Бинарное отношение антирефлексивно если для каждого элемента aϵM отношение aRa не выполняется (отношение «быть сыном»)
В) Симметричность
Отношение R симметрично если для любой пары <a,b>ϵMxM Бо выполняется в обе стороны – aRb и bRa (отношение «учиться в одном колледже»)
Г) Антисимметричность
Бинарное отношение R антисимметрично, если ни для каких различающихся элементов a и b не выполняется aRb, bRa (отношение «быть начальником»)
Д) Транзитивность
Бинарные отношения транзитивны, если для любых элементов a,b,c выполняется aRb и bRc => aRc (отношение «быть братом»)
29. Отношение эквивалентности.
Отношением эквивалентности называется бинарное отношение, если оно обладает свойствами рефлексивности, симметричности и транзитивности)
30. Отношение порядка
Отношением порядка называется бинарное отношение, если оно обладает свойствами рефлексивности, антисимметричности и транзитивности.
Предикаты
31. Что называется предикатами, примеры предикатов
Предика́т
(n-местный,
или n-арный) —
это функция с множеством значений {0,1}
(или «ложь» и «истина»), определённая
на множестве
![]() (произвольном
множестве). Таким образом, каждый набор
элементов множества M
характеризуется либо как «истинный»,
либо как «ложный».
(произвольном
множестве). Таким образом, каждый набор
элементов множества M
характеризуется либо как «истинный»,
либо как «ложный».
Предикат P(x1,..xn)=1 – называется тождественно истинным.
Предикат P(x1,..xn)=0 – называется тождественно ложным.
Т.к. предикаты принимают значения только из множества {0;1} к ним применимы все свойства булевой алгебры.
Пример:
Предикат ЛЮБИТ(x,y) для отношения «x любит y»
