Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский государственный национальный исследовательский университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Глава1,2,3,4.doc

Скачиваний:

Добавлен:

01.12.2018

Размер:

1.25 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 67 / 87 8 > Следующая >>>

4.2. Решение системы линейных уравнений с помощью обратной матрицы

Рассмотрим систему n уравнений с n неизвестными

(4.5)

Обозначим:

, ,

где A - матрица коэффициентов при переменных, или матрица системы, X - матрица-столбец переменных, B -матрица-столбец свободных членов. В матричной форме система (4.5) выглядит так:

. (4.6)

Если матрица A невырожденная, т.е. определитель системы , то для матрицы A существует обратная . Умножая обе части уравнения (4.6) на матрицу слева, получим

Поскольку , а , то решение системы (4.6) дает формула

. (4.7)

Пример 4.1. Решить систему уравнений с помощью обратной матрицы:

Обозначим , , .

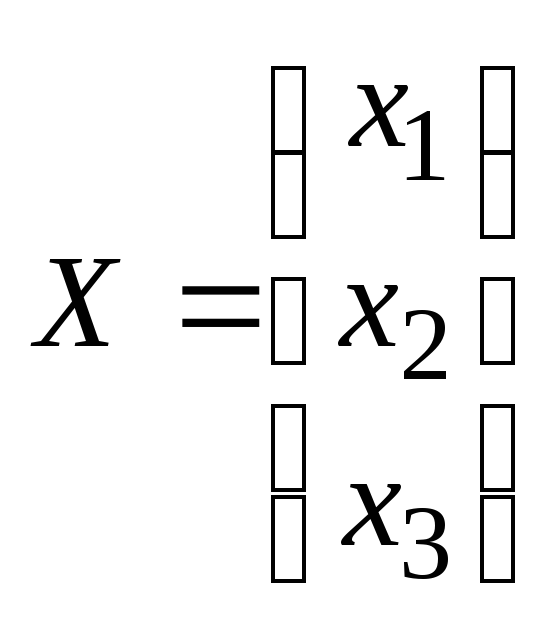Вычислим определитель матрицы A:

, т.е. матрица A невырожденная и метод применим.

По алгоритму, изложенному в п.3.3 (см. пример 3.12)найдем обратную матрицу :

Вычисляем алгебраические дополнения

, ,

Вычисляем обратную матрицу

По формуле (4.7) получаем решение системы:

т.е. решение системы , , .

4.3. Правило Крамера

Рассмотрим систему n уравнений с n неизвестными (4.5) с невырожденной матрицей системы.

Т е о р е м а К р а м е р а: Пусть - определитель матрицы системы, а - определитель, получаемой из определителя заменой j-го столбца столбцом свободных членов. Тогда, если , то система имеет единственное решение, определяемое по формулам:

. (4.8)

Формулы (4.8) получили название формул Крамера.

С л е д с т в и е : Если система (4.5) несовместная или неопределенная, то .

Пример 4.2. Решить систему уравнений по формулам Крамера:

Вычислим определитель матрицы A:

, т.е. матрица A невырожденная и метод применим. По теореме Крамера система имеет единственное решение.

Вычислим определители ,,, последовательно заменяя в первый, второй и третий столбцы столбцом свободных членов. Получим:

, ,

т.е. решение системы (1, -2, 3).

4.4. Метод Гаусса

Данный метод является самым общим, применимым для любых систем m линейных уравнений с n переменными (4.4).

Метод Гаусса – метод последовательного исключения неизвестных – заключается в том, что при помощи элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида. Алгоритм метода состоит из двух частей, называемых прямым и обратным ходом.

Прямой ход – это последовательность действий по приведению системы уравнений к ступенчатому виду.

Шаг 1. Предположим, что коэффициент системы (4.4) отличен от нуля (если , поставим на первое место уравнение, в котором коэффициент при переменной не равен нулю). Затем, умножая первое уравнение последовательно на числа и прибавляя полученные уравнения соответственно ко второму, третьему, му уравнению системы (4.4), исключим неизвестное из всех уравнений, начиная со второго. Система уравнений примет вид:

(4.9)

Шаг 2. Предположим, что коэффициент системы (4.9) отличен от нуля (если , переставим уравнения в системе так, чтобы коэффициент при переменной во втором уравнении не был равен нулю). Затем, умножая первое уравнение последовательно на числа и прибавляя полученные уравнения соответственно ко третьему, четвертому, му уравнению системы (4.9), исключим неизвестное из всех уравнений, начиная с третьего. Система уравнений примет вид:

(4.10)

Продолжим процесс последовательного исключения неизвестных далее. В результате преобразований могут получиться уравнения вида (4.3), которые можно вычеркнуть, после чего число уравнений в системе уменьшится. Возможно также, что в результате преобразований получится уравнение вида (4.2), которое является противоречивым. В этом случае система является несовместной. Если уравнение вида (4.2) не встретится, не более чем через шагов прямого хода система примет ступенчатый вид:

(4.11)

Для упрощения записи в системе (4.11) опущены индексы над коэффициентами. Число не превосходит число , т.к. в процессе преобразований возможно уменьшение числа уравнений из-за вычеркивания уравнений вида (4.3). Характерным для системы (4.11) является то, что диагональные коэффициенты , а коэффициенты , , расположенные ниже диагонали, равны нулю. Возможны два случая: и .

Если , то система (4.11) примет треугольный вид

(4.12)

Обратный ход – это процедура нахождения решения системы , когда неизвестные определяются последовательно, начиная с последнего уравнения и до первого.

1. Случай . Поскольку , из последнего уравнения системы находим

Подставив полученное значение в предпоследнее уравнение системы (4.12), найдем значение неизвестного . Затем, подставляя найденные значения в вышестоящее уравнение, находим и т.д. Наконец из первого уравнения получим . Таким образом, в случае система имеет единственное решение.

2. Случай . Из последнего уравнения выразим неизвестное через неизвестные :

Подставив выражение в предпоследнее уравнение, найдем и остальные неизвестные (аналогично первому случаю). В результате неизвестные будут выражены через неизвестные, т.е. получим систему

(4.13)

которая называется общим решением исходной системы уравнений. Неизвестные называются базисными, а - свободными. Задавая значения свободных неизвестных, из общего решения можно получить соответствующее частное решение системы. Таким образом, в случае система имеет бесконечное множество решений.

Метод Гаусса удобно реализовать в матричной форме. Для этого все коэффициенты и свободные члены системы уравнений записывают в расширенную матрицу системы. Каждому элементарному преобразованию системы линейных уравнений соответствует преобразование ее расширенной матрицы.

Пример 4.3. Решить систему уравнений методом Гаусса:

Составим расширенную матрицу системы, для удобства отделим столбец свободных членов от матрицы системы вертикальной чертой. Подвергнем ее элементарным преобразованиям:

~ ~ ~ ~ .

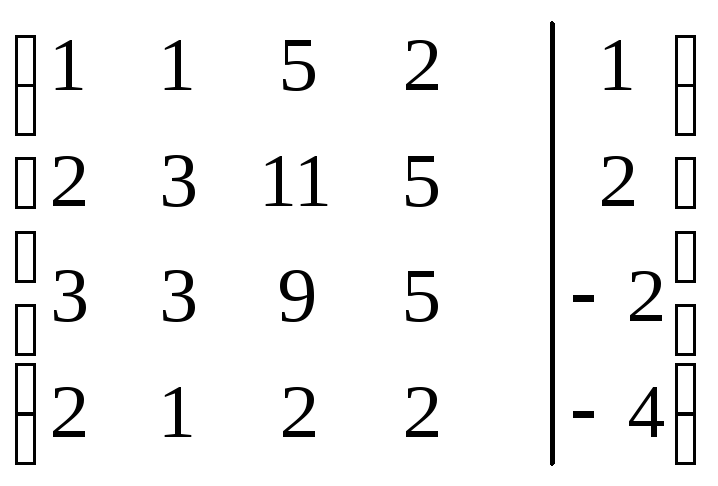Сначала мы поменяли местами первую и вторую строки, затем получили нули в первом столбце (для этого первую строку умножили последовательно на -2 , -3, -2 и прибавили ко второй, третьей и четвертой строкам). Затем получили нули во втором столбце, для чего прибавили вторую строку к четвертой. Наконец, к четвертой строке прибавили третью строку, умноженную на . Получили расширенную матрицу системы треугольного вида, следовательно, система имеет единственно решение, которое найдем обратным ходом метода.

Из последнего уравнения находим . Из предпоследнего уравнения выражаем , откуда находим . Затем выражаем , откуда находим , и, наконец, из первого уравнения получаем , или . Подстановкой можно убедиться в правильности найденного решения.

Пример 4.4. Решить систему уравнений

Составим расширенную матрицу этой системы, после чего выполним соответствующие шаги прямого хода метода Гаусса. Получим

~~.

Уравнение 0 = -26 не имеет решений, следовательно, данная система несовместна.

Пример 4.5. Решить систему уравнений

~ ~ ~~.

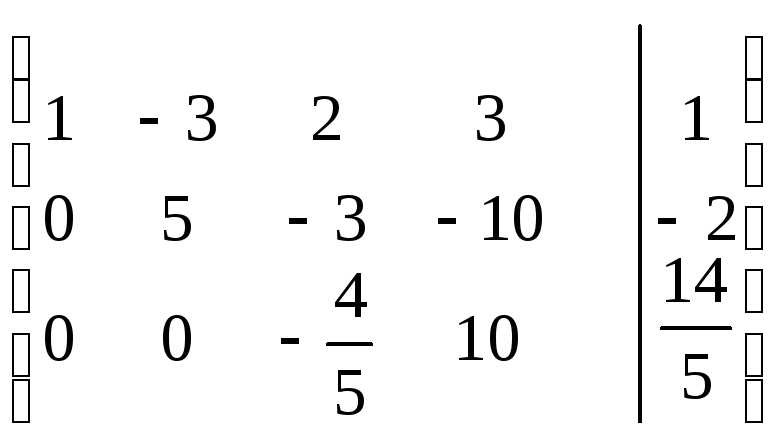Полагая неизвестную свободной, а неизвестные базисными, обратным ходом метода Гаусса находим общее решение системы уравнений:

Поскольку неизвестная может принимать любые значения, данная система имеет бесконечное множество решений. Например, найдем частное решение, соответствующее значению . Подставим в общее решение, получим , , .