Принцип двойственности

Функция f*(x₁,…,x_n)=называется двойственной к функции f. Из определения следует, что f**=(f*)*=f, т.е. функция f двойственна к f* и наоборот.

5. (0)*=1, (xy)*=x&y, (x)*=x, (x)*= x.

2. Пусть F(x₁,…,x_n)=f(f₁(x₁,…,x_n),…, f_m(x₁,…,x_n)), тогда F*(x₁,…,x_n)=f*(f₁* (x₁,…,x_n),…, f_m* (x₁,…,x_n))

Из этой леммы следует принцип дойственности:

Если формула A=S[f₁,…,f_k] реализует функцию f(x₁,…,x_n), то S[f₁*,…,f_k*] реализует функцию f*(x₁,…,x_n).

Двойственная к A формула обозначается A*=S[f₁*,…,f_K*]. Таким образом, в силу принципа двойственности формула, двойственная к данной, получается заменой в исходной формуле всех функций на двойственные с сохранением ее строения, т.е. порядок выполнения операций остается прежним.

6. Найдем (xyyzzx)*. В силу принципа двойственности, т.к. & двойственна , и наоборот, имеем (xyyzzx)*=(xy)(yz)(zx)=(yxz)(zx)=xyyzzx.

В силу принципа двойственности из эквивалентности формул A₁ и A₂ следует эквивалентность двойственных формул A₁* и A₂*.

Задачи

9. Используя непосредственно определение двойственности, выяснить, является ли функция g двойственной к функции f:

   1. , ;

   2. , ;

   3. , ;

   4. , ;

   5. , ;

   6. , ;

   7. , ;

   8. , ;

   9. , ;

   10. , .

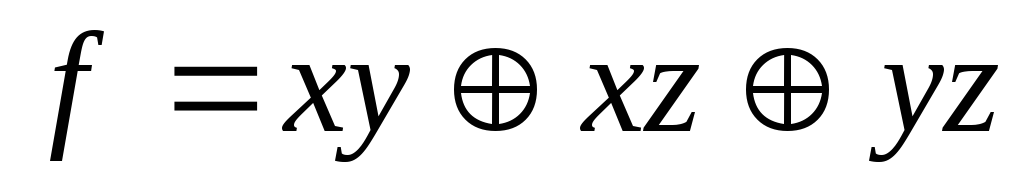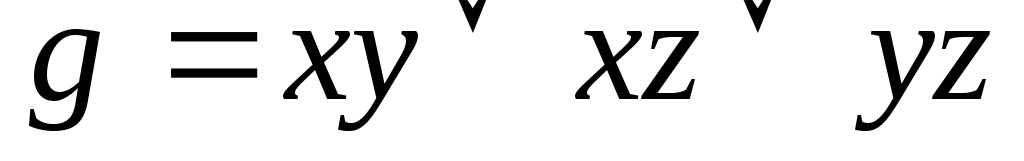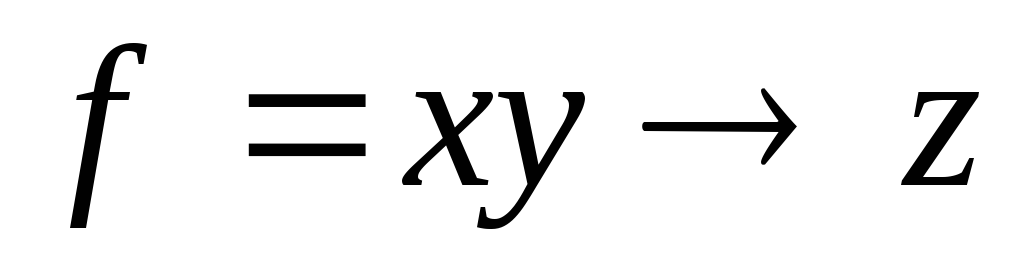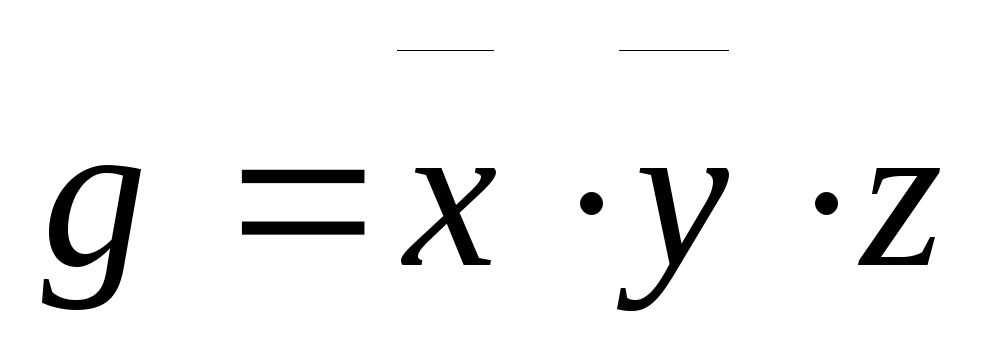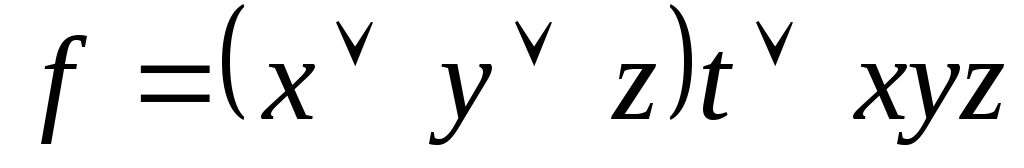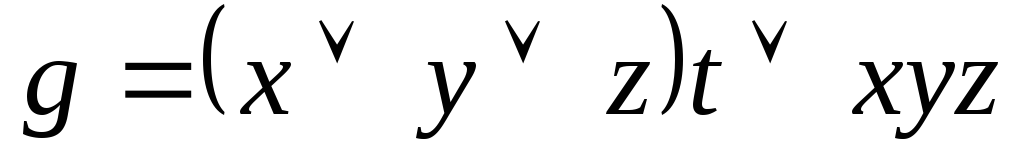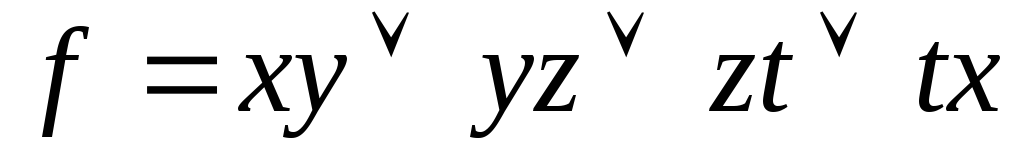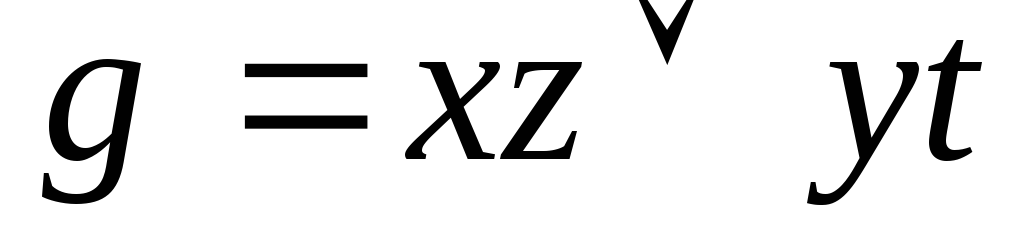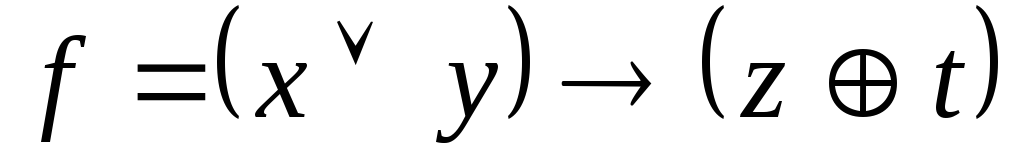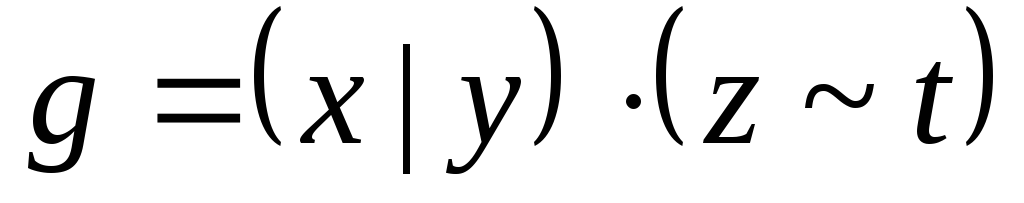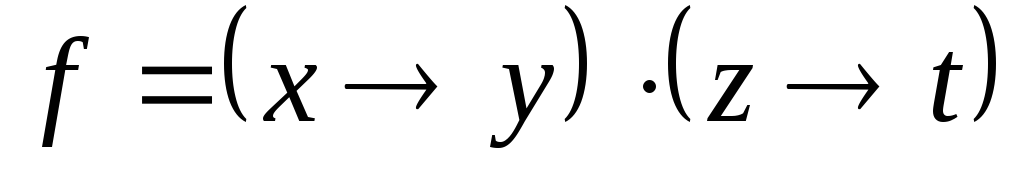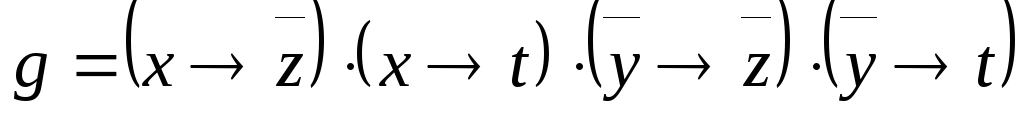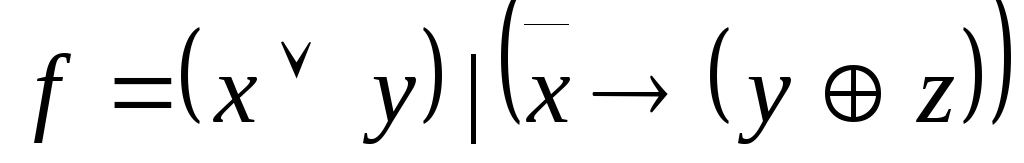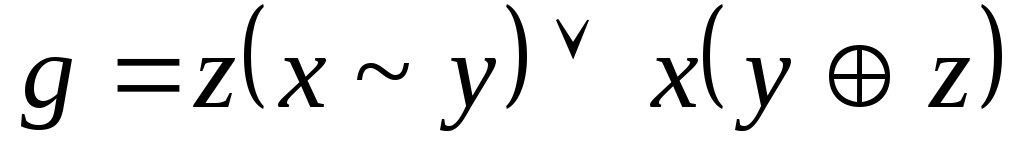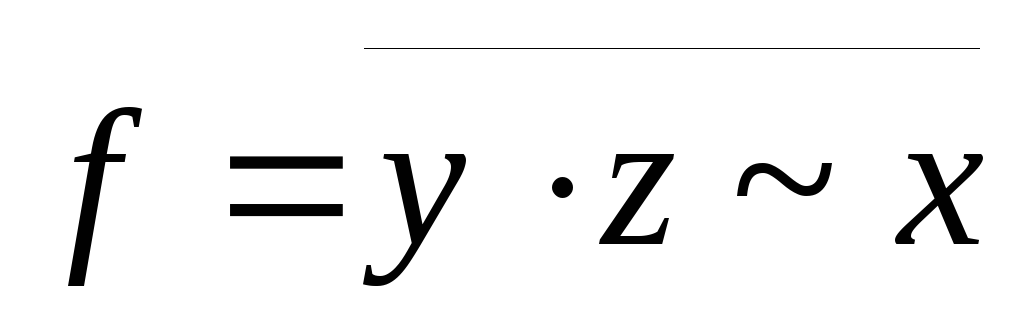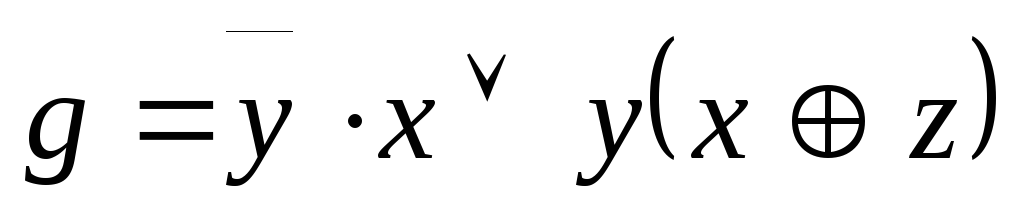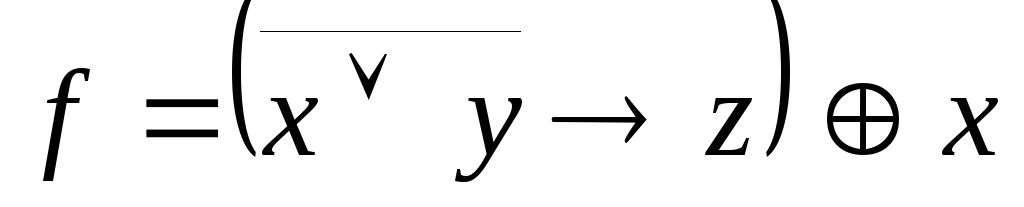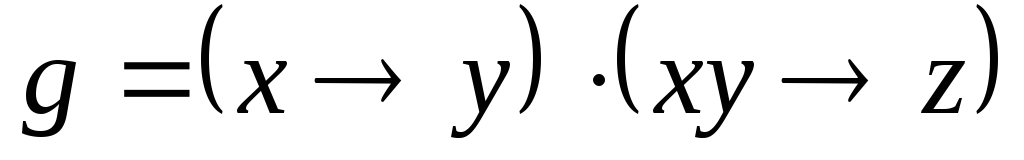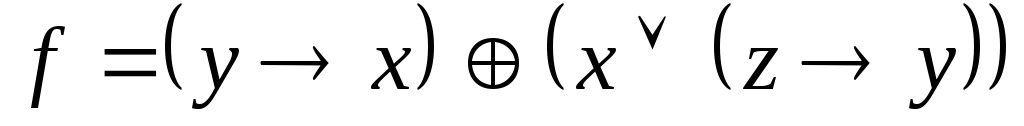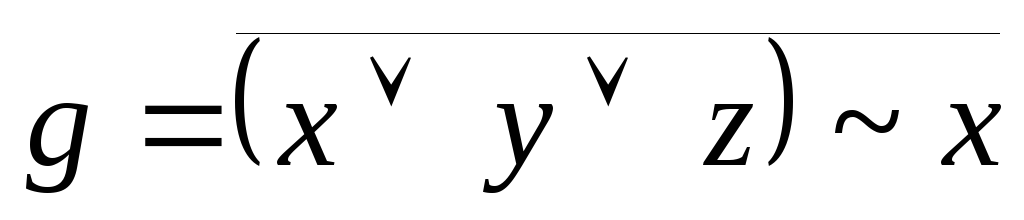10. Используя принцип двойственности, построить формулу, реализующую функцию, двойственную к функции f, и убедиться, что она эквивалентна формуле A:

    1. , A=;

    2. , A=;

    3. , A=;

    4. , A=;

    5. , A=;

    6. , A=;

    7. , A=;

    8. , A=;

    9. , A=;

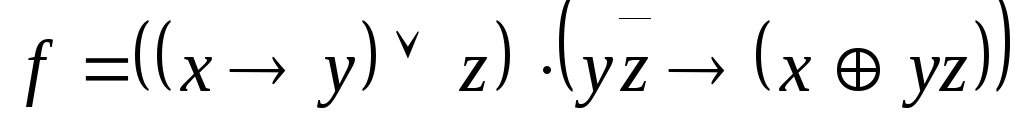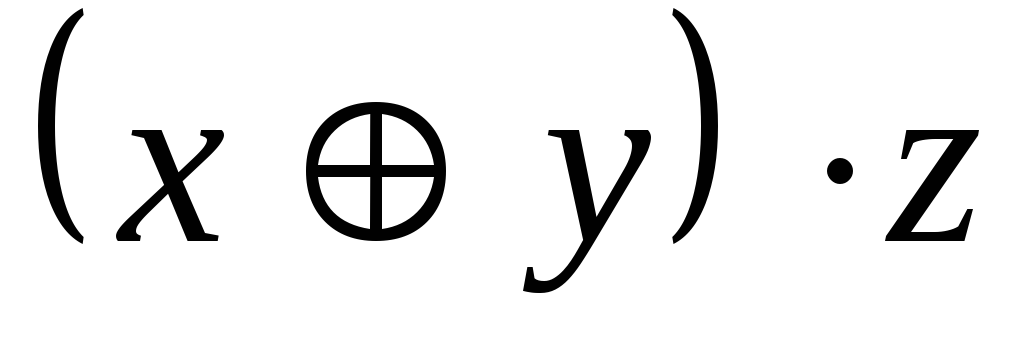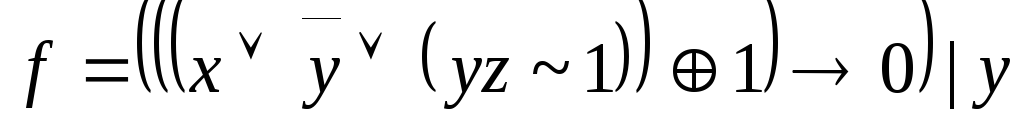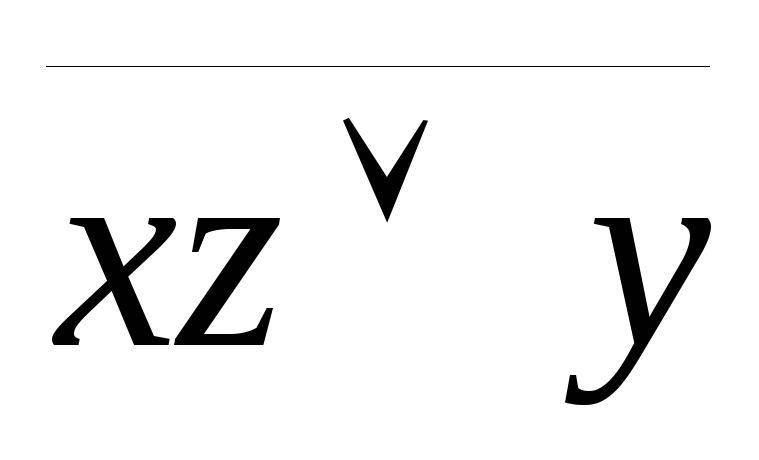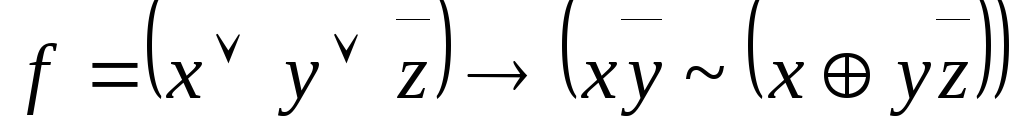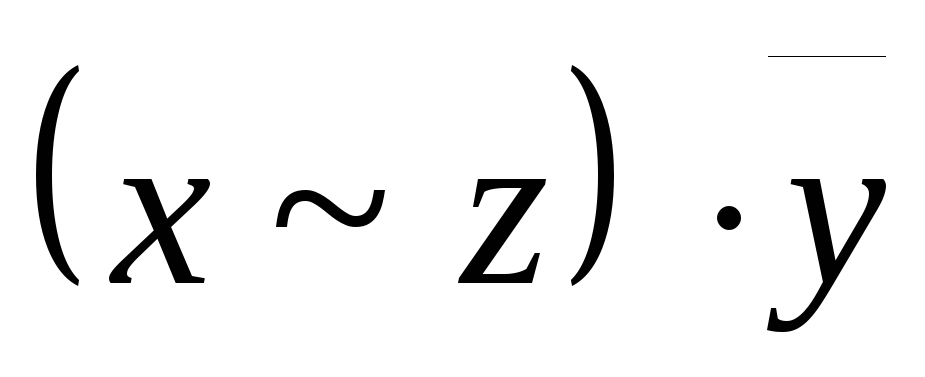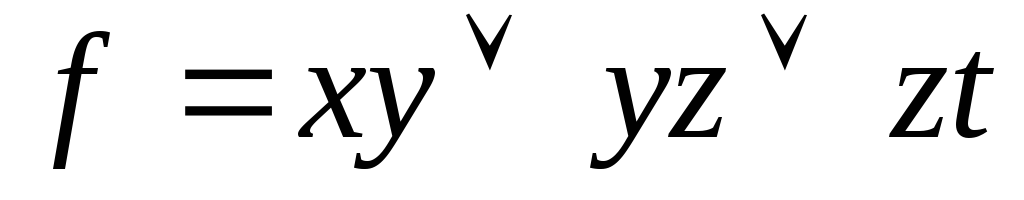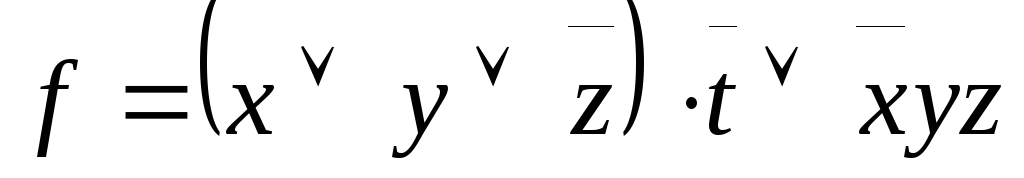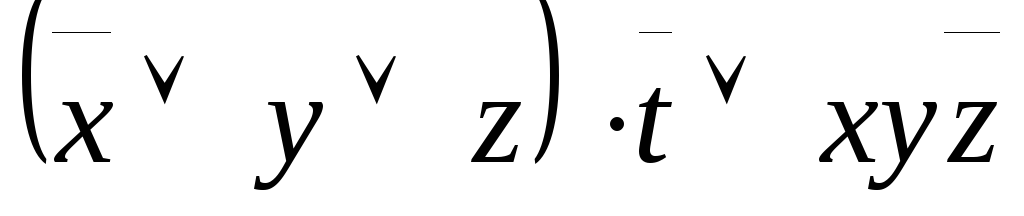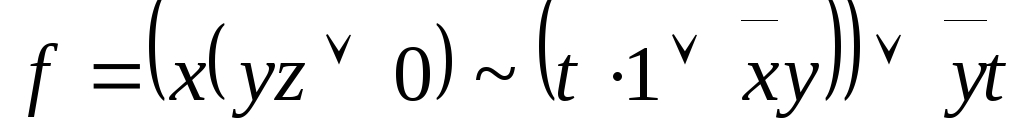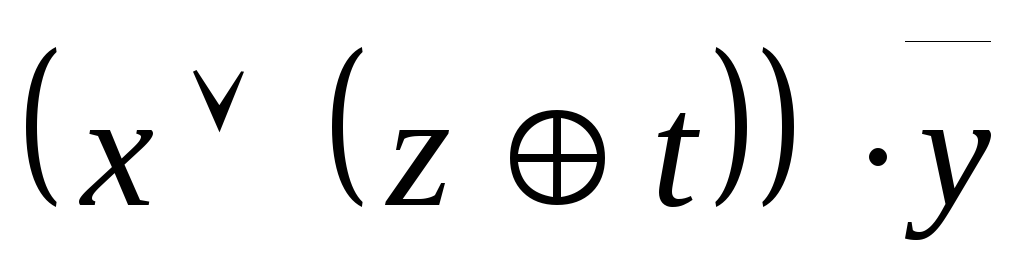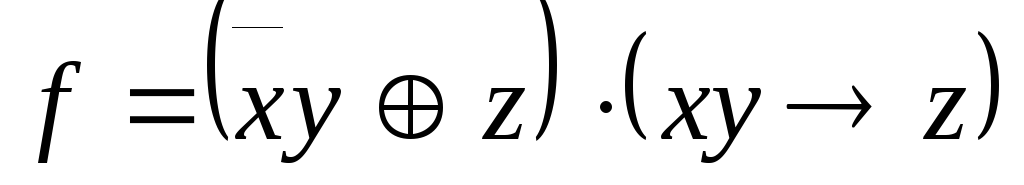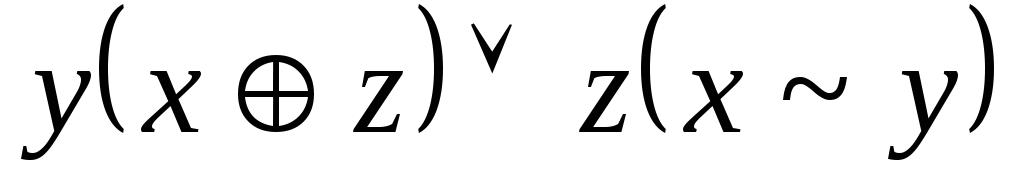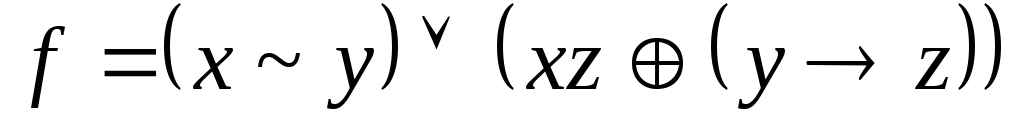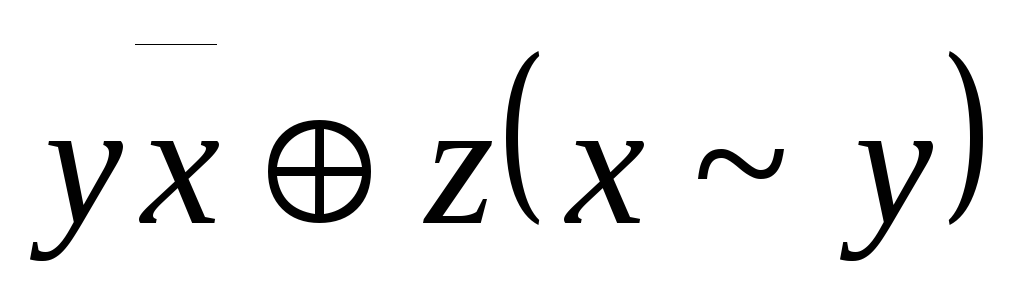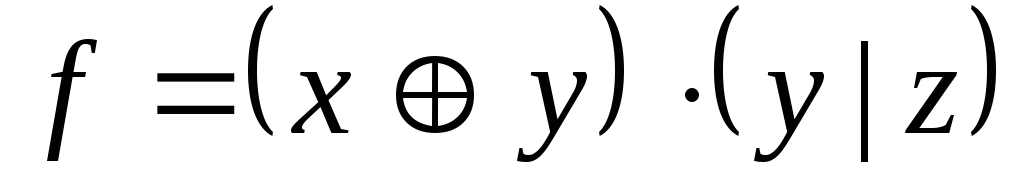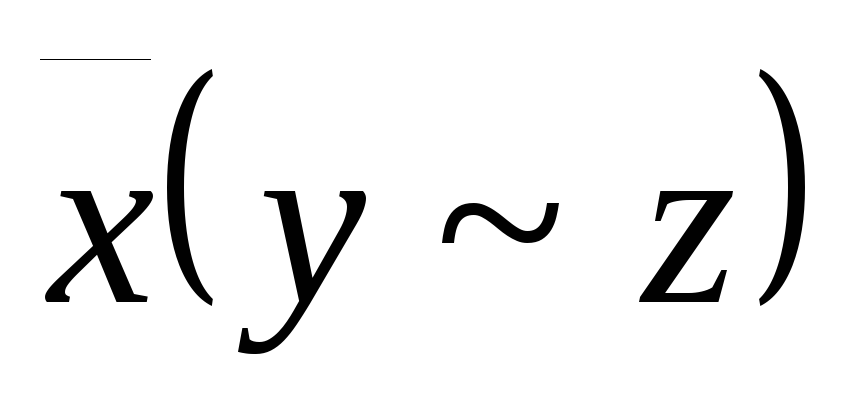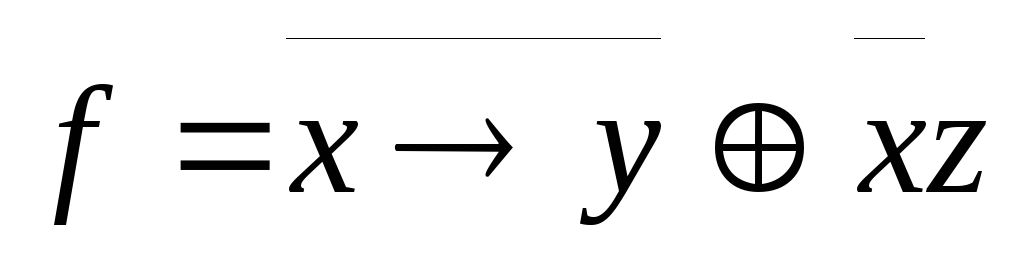    10. , A=.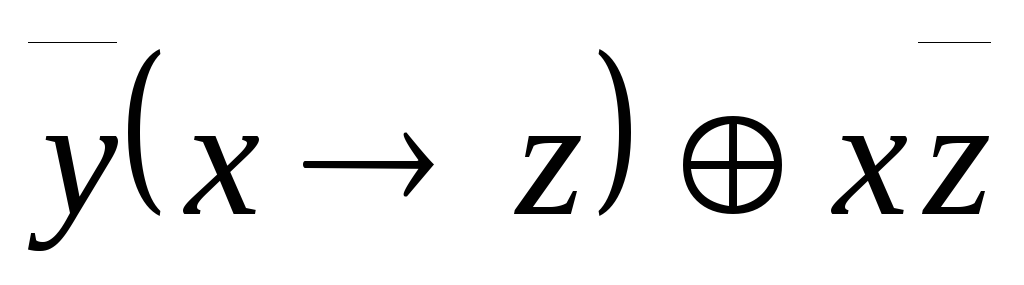

Разложение булевых функций по переменным

Введем новую функцию

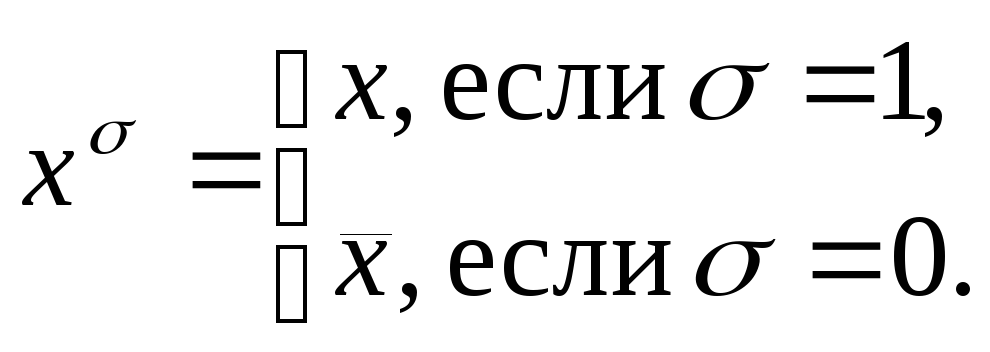
Очевидно, что .

Конъюнкции вида и дизъюнкции вида называют элементарными. Число m называется рангом элементарной конъюнкции (дизъюнкции). Дизъюнкция элементарных конъюнкций называется дизъюнктивной нормальной формой или д.н.ф. Конъюнкция элементарных дизъюнкций называется конъюнктивной нормальной формой или к.н.ф.

1. Всякая булева функция f(x₁,…,x_n) для любого m, 1mn, представима в виде f(x₁,…,x_n)= .

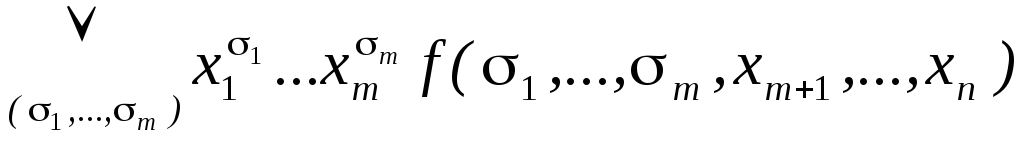Это представление называется разложением булевой функции по первым m переменным. Функцию, получаемую из f, подстановкой на места переменных x₁,…,x_m констант ₁,…,_m, называют -компонентой функции f.

Следствие 1. Для любого i, 1in,

f(x₁,…,x_n)=

Следствие 2. Если f(x₁,…,x_n)0, то f(x₁,…,x_n)=.

Это разложение называется совершенной д.н.ф. (с.д.н.ф.).

2. Всякая булева функция может быть представлена формулой в базисе Б={,,}.

3. Если f(x₁,…,x_n)1, то f(x₁,…,x_n)=.

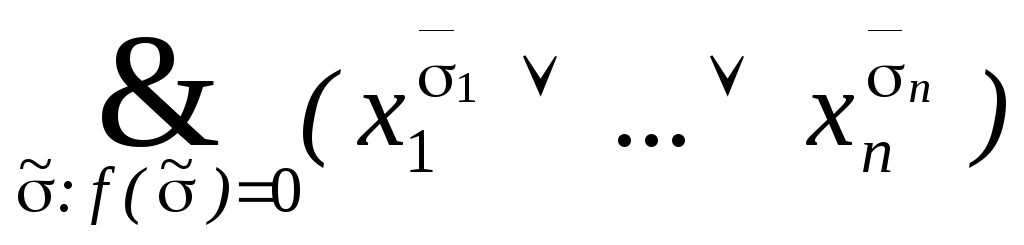Это разложение называется совершенной к.н.ф. (с.к.н.ф.).

Рассмотрим алгоритмы построения с.д.н.ф. и с.к.н.ф.

Алгоритм построения с.Д.Н.Ф. По таблице значений функции.

1. Выбрать строку, в которой функция равна 1.

2. Построить элементарную конъюнкцию, включая в нее с отрицанием те переменные, которые в этой строке равны 0.

3. Перейти к следующей строке таблицы, на которой функция равна 1.

4. После перебора всех строк составить с.д.н.ф. из полученных конъюнкций.