
- •Контрольна робота №2 Зразок розв`язання і оформлення контрольної роботи №2
- •1. Побудувати дискретний розподіл частот і відносних частот.
- •Варіанти завдань контрольної роботи №2
- •Завдання 2.2. Знайти розв’язок задачі Коші диференціального рівняння першого порядку:
- •2.3. Визначити ймовірності подій за класичною моделлю
- •Завдання 2.4. Імовірності суми й добутку подій
- •Література
Контрольна робота №2 Зразок розв`язання і оформлення контрольної роботи №2
Варіант № 31
Завдання 2.1. Розв’язати диференціальні рівняння:
а)
![]() ,
б)
,
б)
![]() .
.
Розв’язання.
а) Рівняння
![]() є рівнянням з відокремлюваними змінними
.
є рівнянням з відокремлюваними змінними
.
Для
відокремлення змінних, поділимо обидві
частини рівняння на добуток
![]() ,
в результаті чого отримаємо диференціальне
рівняння
,
в результаті чого отримаємо диференціальне
рівняння
![]() .
.
Інтегруємо останнє рівняння
![]() ,
,
![]() ,
,
![]() - загальний інтеграл
заданого рівняння.
- загальний інтеграл
заданого рівняння.
б)
Рівняння
![]() записане в загальній формі. Виразимо з
нього
записане в загальній формі. Виразимо з
нього
![]() і отримаємо рівняння в нормальній формі
і отримаємо рівняння в нормальній формі
![]() .
.
Це рівняння є однорідним диференціальним рівнянням. Дійсно,
![]() .
.
Для
розв’язання однорідного рівняння
введемо заміну
![]() ,
тоді
,
тоді
![]() ;
;
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]()
![]() .
.
Повертаючись до
змінної
![]() ,
знаходимо загальний інтеграл
заданого рівняння:
,
знаходимо загальний інтеграл
заданого рівняння:
![]() або
або
![]() .
.
Завдання 2.2. Знайти розв’язок задачі Коші диференціального рівняння першого порядку
![]() .
.
Розв’язання. Задача Коші полягає в тому, щоб визначити частинний розв’язок диференціального рівняння, використовуючи для цього початкову умову. Для цього спочатку знаходимо загальний розв’язок диференціального рівняння.
Задане
рівняння є лінійним (![]() і
і
![]() містяться в рівнянні лише в
перших степенях) . Розв’язуємо його
методом Бернуллі. За формулою маємо
містяться в рівнянні лише в
перших степенях) . Розв’язуємо його
методом Бернуллі. За формулою маємо
![]() ,
,
![]() .
.![]()
![]() ,
,
![]() .
.
Складаємо систему двох рівнянь:

Розв’язуємо перше з рівнянь системи:
![]()
![]()
![]() ,
,
![]() .
.
Підставляємо
отримане значення функції
![]() в друге рівняння системи і розв’язуємо
його:
в друге рівняння системи і розв’язуємо
його:
![]()
![]()
![]() ,
,
![]() .
.
Запишемо загальний розв’язок диференціального рівняння
![]() .
.
Для
розв’язання задачі Коші
застосуємо початкову умову і знайдемо
значення сталої
![]() ,
для чого підставимо в загальний розв’язок
значення
,
для чого підставимо в загальний розв’язок
значення
![]() ,
,
![]() :
:
 .
.
Отже, частинний розв’язок диференціального рівняння має вигляд
![]() .
.
Завдання 2.3. Визначити ймовірності подій за класичною моделлю.
Група з 24 студентів, серед яких 5 відмінників, довільно розбивається порівну на дві підгрупи. Знайти ймовірність того, що три відмінники будуть у першій підгрупі (подія А).
Розв’язання. Будемо випадково відбирати 12 студентів у першу підгрупу. Побудуємо класичну модель досліду, в якому кожен випадок – це один із варіантів розподілу студентів. Якщо послідовність відбору не береться до уваги, то загальне число п випадків у такій моделі дорівнює числу різних комбінацій із 24 по 12:
![]() .
.
Серед знайденого числа способів комплектування першої підгрупи знайдемо число варіантів т, сприятливих події А. Це такі варіанти, у яких 3 студенти взяті серед 5 відмінників, а решта 9 – серед 19 студентів, що не вчаться на відмінно. Число т знайдемо за комбінаторним принципом добутку
![]() .
.
Тоді ймовірність попадання трьох відмінників у першу підгрупу обчислюється за класичною формулою:
![]() .
.
Відповідь: 0,34.
Завдання .2.4. Імовірності суми й добутку подій
1). Серед семи виробів є три бракованих. Знайти ймовірність події А, яка полягає в тому, що один за одним без повернення будуть вийняті три вироби у такій послідовності: бракований – не бракований – бракований.
Розв’язання. Позначимо події: А1 – перший узятий виріб бракований; А2 – другий виріб не бракований; А3 – третій виріб бракований. Тоді ймовірність події А можна обчислити за теоремою множення ймовірностей:
![]() .
.
Відповідь: 0,114.
2). Знайти ймовірність влучити в мішень принаймні один раз при трьох пострілах (подія А), якщо ймовірність влучити в мішень при першому пострілі (подія А1) становить 0,7, при другому (подія А2) – 0,8, при третьому (подія А3) – 0,85.
Розв’язання.
Перейдемо до протилежної події –
стрілець не влучив жодного разу в мішень
із трьох пострілів (подія
![]() ).
Тоді
).
Тоді
![]() .
Оскільки події
.
Оскільки події
![]() ,
а разом з ними відповідні протилежні
події – незалежні, то за наслідком
теореми 1
,
а разом з ними відповідні протилежні
події – незалежні, то за наслідком
теореми 1
![]() (1–
0,7)(1– 0,8)(1– 0,85)=0,009,
(1–
0,7)(1– 0,8)(1– 0,85)=0,009,
звідки знайдемо
ймовірність події А :
![]() .
.
Відповідь: 0,991.
Завдання
.2.5.
Функція
розподілу неперервної випадкової
величини
![]() має вигляд:
має вигляд:


а)
Знайти коефіцієнт A
та зробити креслення
![]() ;
б) записати
;
б) записати
![]() та зробити креслення; в) обчислити
числові характеристики
та зробити креслення; в) обчислити
числові характеристики
![]() та
та
![]() ;
г) знайти ймовірність події
;
г) знайти ймовірність події
![]() .
.
Розв’язання.
а) Функція розподілу випадкової величини
![]() неперервна, тому
неперервна, тому
![]() .
Звідси маємо А=1.
Отже, графік функції розподілу має
вигляд (Рис. 2.1):
.
Звідси маємо А=1.
Отже, графік функції розподілу має
вигляд (Рис. 2.1):

Рис.2.1
б)
![]() знайдемо за властивістю 2):
знайдемо за властивістю 2):
![]()
![]()
Графік щільності розподілу наведений на рис. 2.2:

Рис. 2.2
в) За формулами обчислимо числові характеристики:
![]()
![]() .
.
![]() =
=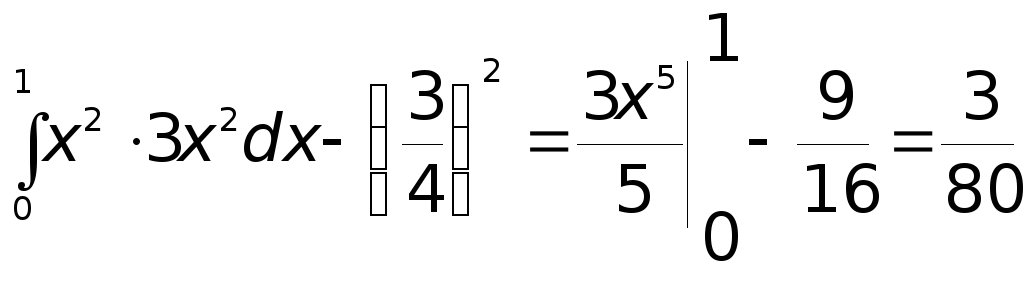 .
.
г) Використовуючи властивість щільності розподілу, одержимо :
P![]() =
= .
.
Або
P![]() =
=![]() .
.
Відповідь:
а) А=1;
б)
![]() в)
в)
![]()
г)
![]()
Завдання 2.6.31. Для даного варіанта задана вибірка
1, 3, 4, 5, 1, 3, 4, 3, 5, 1, 3, 4, 1, 3, 4, 3, 4, 3, 4, 3.
Потрібно:
