шпоргалка / билет / 43-49 билеты

43 Звенья с модулированием сигнала управления

( звенья на переменном токе )

ГНЧ – генератор несущей частоты

Х – моделирует несущую частоту

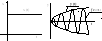
В звеньях с модулированием сигнала управления изучается поведение огибающей кривой.

47 Статическая САР. Статическая точность САР.

Статическая САР показывает насколько точно САР поддерживает выходные корд-у при заданном знач. управляющ. велеч. Ошибка САР появ-я в результате действия возмущения.

Действие возмущ. не зависит от сигн. упр-я. Возмущ. измен-я по произвольн. закону.

Статическая точность обозначается S.

Δy_рег – это отклонение выходн. корд. придейств. возмущ. f в замкн. сист.

Δy_нерег - это отклон. выходн. корд. при таком же действии возмущения в разомкн. сист.

Статизм связан с велечиной К_рс

Δ_рс = Δy_нерег Δ_зс = Δy_рег

Статическая точн. может прест-я в %

Проценты взяты относит. того знач. кот. задано

Структ. схема представл. на рис. может быть преставлена 2-мя видами САР:

1. статическая САР

2. астотическая САР

Статическая САР – это такая САР у кот. все звенья в прям. и обрат. связи позиционные. Точность стат. САР опред-я выраж-м (1). Учитывая, что К_рс нельзя сильно увелич., т.к. САР станов-я неустой-м, статич. САР может только уменьш. ошибку, но полностью её не ликвид-ть.

48 Астатическая САР. Динамическая точность САР.

Астотич. САР отлич-я от стат. тем, что в цепи упр-я астатич-й САР имеется интегратор.

Астат. САР не имеет стат. ошибки.

Особенности астат.САР:

1) Если возмущ. действ-т после интегр-ра , то стат. ошибка вых корд. = 0. Но бывают такие САР у кот. возмущ. действ-т до интегр-ра. В этом случае в астат САР появ-я стат. ошибка.

2) астат. САР может регламент-ть ошибку перех-х проц-в. ( регламентировать – выдерживать на уровне задан-го знач. ) Ошибка перех-х проц-в наз-я динамич. ошибкой ().

- скорость изменен. управ-го сигн.

• Если в астат. САР только 1интегр.

Звено, то гов-т, что

САР содер-т астатизм I-го пор-а или астат. САР I – го пор-а

• Если в астат. САР 2 интегратора вкл. послед-о, то это астат. САР II-го пор-а

Атат. САР II-го пор-а может свести ошибку  к 0, т. е. =0.

49 Устойчивость САР. Основное условие устойчивости ( по Ляпунову )

Устойчивое САР – это такая САР, кот. после внешнего возд-я возвращ-я в исходное сост-е.

Осн. усл. уст. САР. ( по Ляпунову )

Устойч. сист. зависит от её собсв. динамич. св-в, кот. опр-я её однородн. диф. ур-м. Решение:

1) общее

корень хар-го ур-я

Чтобы сист. была устойч. необх.

Это возможно в том случае, если действ. корни и действит. части комплексн. корней будут отрицательн. (« - »)

Это и есть основное условие устойчивости САР.

45 Линейные САР. Передаточная функция разомкнутой и замкнутой САР.

САР – это сист. звеньев соед-х м/у собой и имеющих прямую цепь упр-я и цепь обратной связи, причём сигн. ОС сравнивается с прямой связью с помощью сумматора С. А упр-е прямой цепью осущ-я по ошибке  м/у сигн. задания и сигн. ОС.

Линейное САР – такая в кот. не содержится звенья содержащие в статической хар-ке существенную нелинейность. ( существенная нелинейность – это такая , кот. нельзя линеаризовать.)

Линейное САР содержит звенья с линеаризуемыми статич. хар-ми.

Разновидности ОС:

1) жёсткая ОС – это такая в кот. экв. передаточн. ф. ОС содержит все позиционные звенья.

2) гибкая ОС – Если хотя бы 1 звено в ОС будет диффирин-м, то это гибкая ОС.

Эквивалентная передаточная ф. замкнутой сист. упр.

Часто САУ содер-т неск. контуров упр-я. В этом случае часто треб-я замкн-ю. САУ представить в виде экв. звена.

(+) если САР с ООС (-) если САР с ПОС

Передаточная ф. разомкнутой системы W_рс.

ТАР раб-т с структ. схемой в кот. имеется единичн. ОС

практическая САР теоретическая САР

W_РС – это есть произведение звеньев, наход-ся в прямой цепи упр-я и в цепи ОС до точки размыкания САР.

По W_РС осуществляется анализ и синтез САР.

46 Правило преобразования структурных схем.

Учитывая, что ТАР работает с сист. у кот. только 1 ОС, А структ. сх. могут иметь неск. ОС, в том числе перекрещ-я связи,  правило преобразования таких схем.

Схемы сначала преобразуются в многоконтурные, а потом в одноконтурный.

ПРАВИЛО:

1.

2. x = x₁ = x₂ y = y₁ + y₂ Если сист. содер-т неск. звеньев включ-х паралл-но, то экв. сх. будет равна сумме звеньев.

3. переноса точек ответвления и сумматора

3.1. перемещение точ. ответвления по ходу упр-го сигн.

х₁(р) = х(р)

3.2. перенос точ. ответвления в напр-ии обратно ходу сигн.

4. перенос сумматоров

1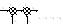) Если сумматоры

оказались на одной

линии, то порядок их

располож-ия не имеет

смысла.

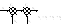примечание:

Если точки ответв.

оказались на одн.

линии, то их порядок

располож. так же не

имеет знач.

2) 1) перенос сумматора по ходу сигн

2) перенос сумматора в противоп. напр. по ходу сигн.

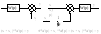
3. перенос точки ответвления ч/з сумматор

при переносе сумматоров и точек ответвления нельзя переносить сумматор ч/з точку отв. и точ. отв. ч/з сумматор.

44 Элементарный объект управления

Больш-во реальн. объектов многомерны, поэтому при постр. САПР необх. многомерн. объекты предст-ть в виде одном-го.

1. Из множества вых-х коор-т выбир-т ту, кот. необх. регул-ть.

2. Выбир-я единств-е упр-щее возд-ие. Это упрывл-щее возд-ее должно наиболее эффект-но среди др. действ-ть на вых-е пар-ры. Возмущ-я ост-я те же.

3. Те упр-щие корд-ты, кот не исполь-но при управл-ии одномерн. объектом , они переходят в разряд входн. парам-в. Те упр-щие воздей-я. кот. перешли в разряд входных парам-в, счит-т, что в проц-е исполья-я остаются постоянными.

Это и есть элементарный ОУ, у кот. вых-я коор-а регулир-я входн. корд. и прирощен-ми f , но при всём этом вых-я коор-а ни какого возд-я на вход-й неимеет.