
Обчислити першу квадратичну форму поверхні:
-
x=rcosucosv, y=rcosvsinu, z=rsinv.
-
x=acosucosv, y=bsinucosv, z=csinv (еліпсоїд).
-
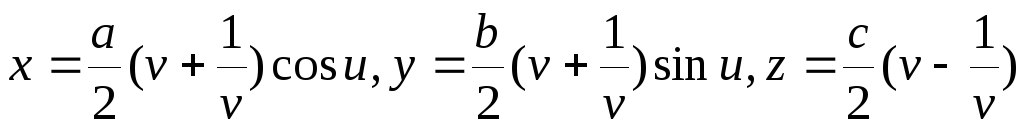 (однопорожнинний
гіпербалоїд).
(однопорожнинний
гіпербалоїд). -
x=acosu, y=bsinu, z=v.
-
x=(u+v)
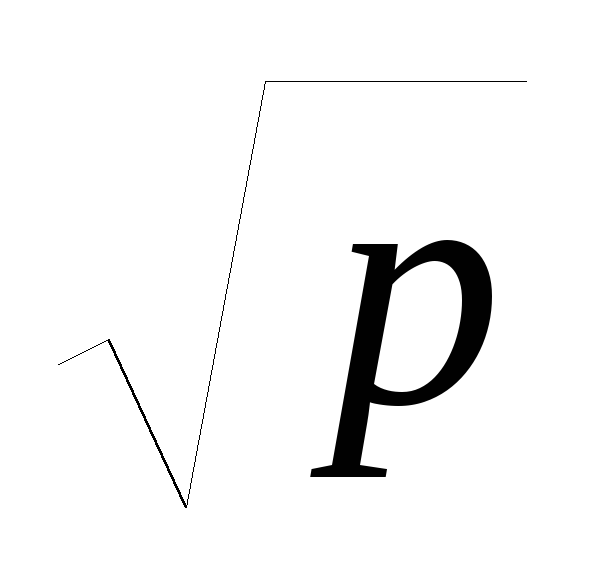 ,
y=(u-v)
,
y=(u-v)
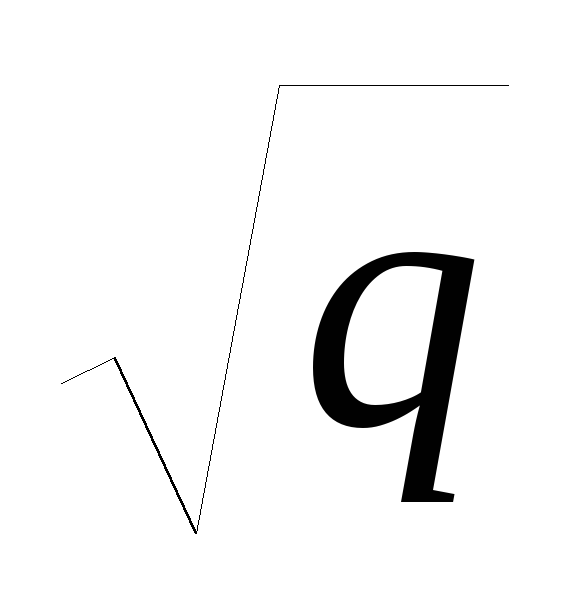 ,
z=2uv.
,
z=2uv. -
x=avcosu, y=bvsinu, z=cv.
-
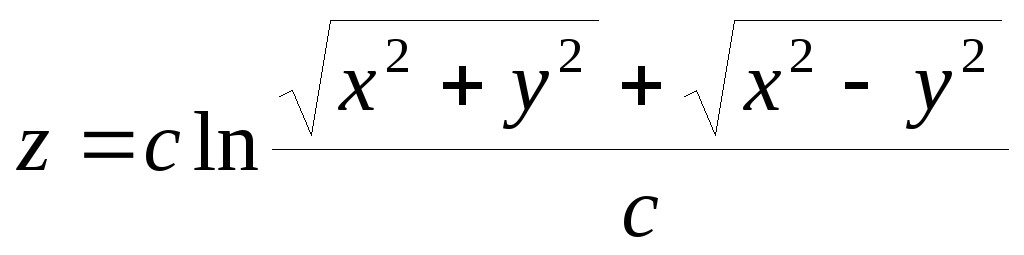 .
. -
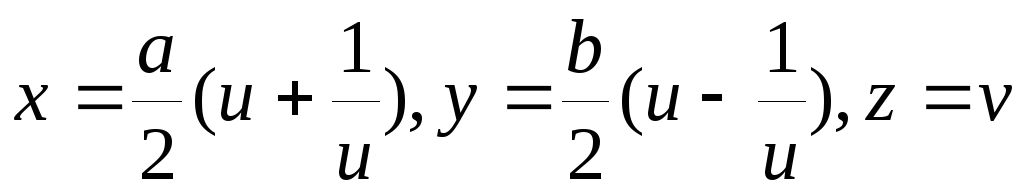 .
.
-
Знайти повну кривину поверхні
-
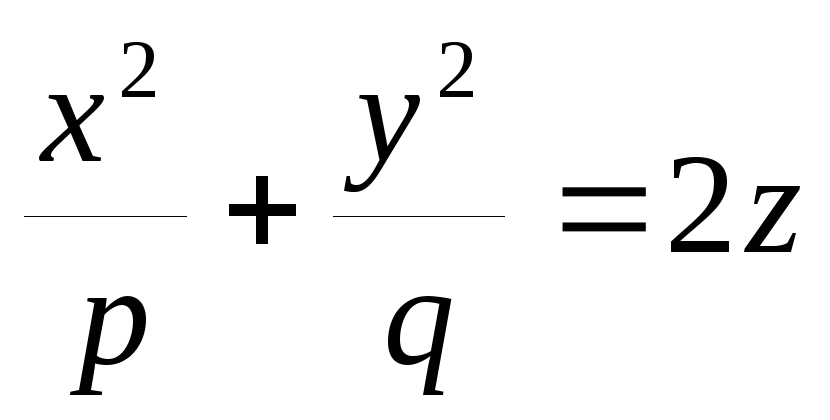 .
. -
x=acosusinv, y=asinusinv, z=cosv (еліпсоїд обертання).
-
x=cos2ulntg
 ,
y=sinucosv, z=sinusinv (псевдосфера).
,
y=sinucosv, z=sinusinv (псевдосфера). -
z=lncosx-lnsiny, повна кривина поверхні дорівнює нулю. Довести.
-
Скласти рівняння дотичної площини і нормалі до гелікоїда:
x=vcosu, y=vsinu, z=ku (у будь-якій точці).
-
Показати, що середня кривина катеноїда рівна нулю:
![]() .
.
-
Скласти рівняння дотічної площини і нормалі до поверхні у точці:
-
x2+z2+a2y2-r2x2=0 (x,y,z).
-
xyz=a3.
-
Обчислити повну і середню кривину поверхні
x=3u+3uv2-u3, y=v3-3v-3u2v, z=3(u2-v2).
-
Знайти першу і другу квадратичні форми поверхні
-
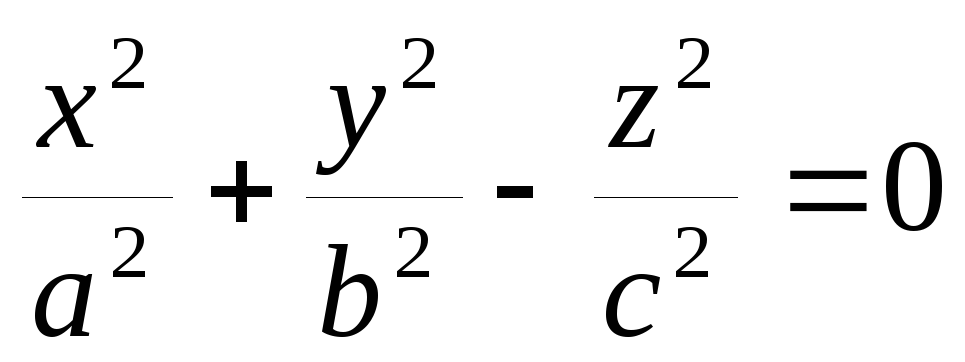 .
. -
 .
.
-
Скласти рівняння площини, що дотікається до поверхні
x2-5y2-z2-4xy-6yz-4x-2y-6z+8=0.
-
Показаті, що всі дотичні площини поверхні, заданої рівнянням проходять через початок координат
z=x![]()
![]() .
.
-
Показати, що нормалі поверхні x
 (u)cosv,
y=
(u)cosv,
y= (u)sinv,
z=
(u)sinv,
z= (u)
перетінають
вісь Z.
(u)
перетінають
вісь Z. -
До поверхні xyz=1 провесті дотічну площіну, паралельну площині x+y-z-3=0.
-
Знайти площу дільниці гвинтової поверхні x=(u-1)cosv, y=(u-1)sinv, z=2
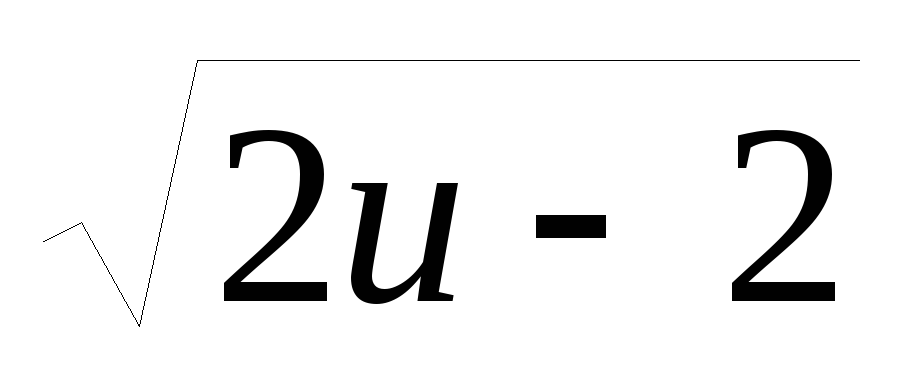 +v,
що
відповідає зміні параметров в області
+v,
що
відповідає зміні параметров в області
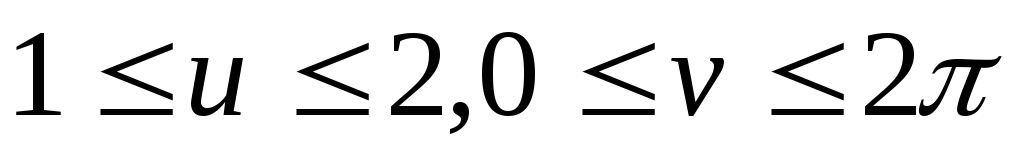 .
. -
Довести, що дотичні площини до поверхні xyz=a3.
-
Знайти площу дільниці гвинтової повезхні x=tgucosv, y=tgusinv, z=
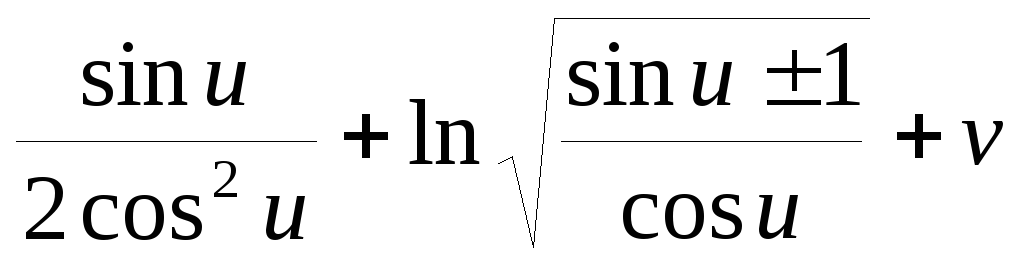 ,
що відповідає зміні параметров в області
,
що відповідає зміні параметров в області
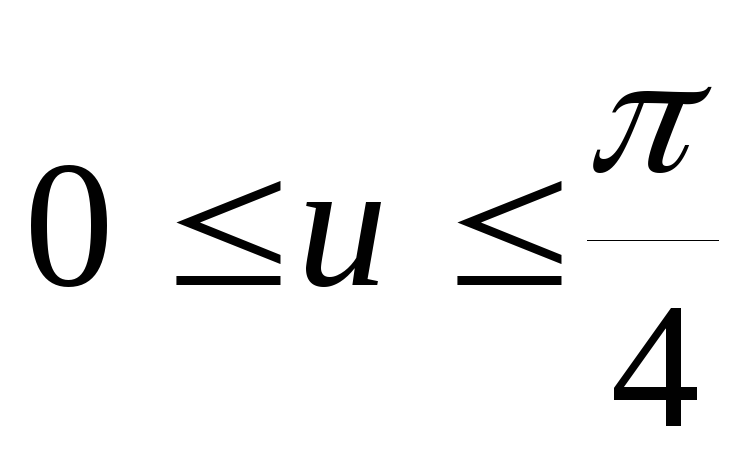 ,
,
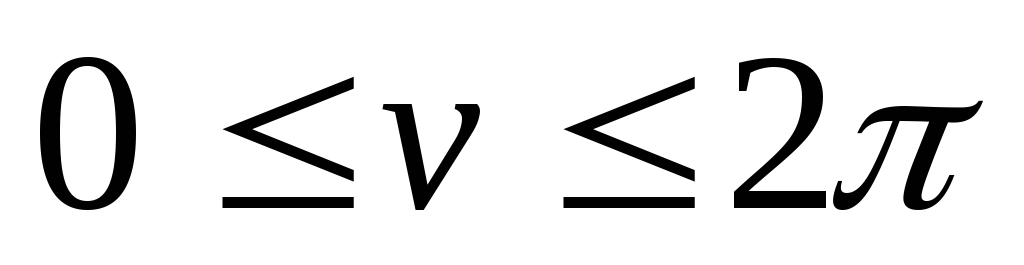 .
. -
Долвести, що на поверхні x2/3+y2/3+z2/3=a2/3 сума квадратів відрізків, що відтинаються дотичними площинами на осях, є величина постійна.
-
Знайти площу чотирикутника на гелікоїді x=aucosv, y=ausinv, z=bv, обмеженого кривими u=0, u=
 ,
v=0, v=1.
,
v=0, v=1. -
Обчислити об’єм пераміди обмеженої площинами координат і дотичною площиною до поверхні a2y2-x2y2-c2z2=1.
-
Показати, що сума квадратів відрізків, які відтинаються на осях кооррдинат дотичними площинами до поверхні x=u3sin3v, y=u3cos3v, z=(a2-u2)3/2, постійна.
