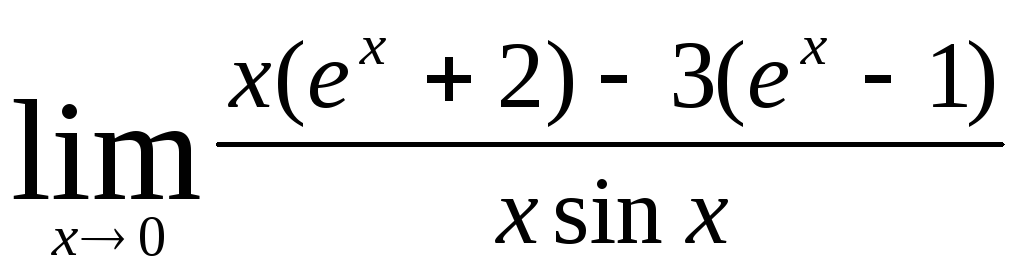- •Содержание
- •Предисловие
- •Глава 3 содержит следующие темы: комбинаторика, бином Ньютона, математическая индукция и комплексные числа Приведены основные формулы и методы решения задач.
- •Глава 4 содержит индивидуальные домашние задания по основным темам курса математического анализа, изучаемым в первом семестре
- •Глава 5 посвящена семинарским занятиям. Приводится перечень основных вопросов, рассматриваемых на семинаре, задачи, которые необходимо решать на семинаре и задачи для самостоятельной работы.
- •Глава 3. Введение в анализ
- •§3.1. Комбинаторика и бином Ньютона
- •1. Комбинаторика
- •2. Число размещений (без повторений) из n элементов по к
- •4. Размещения с повторениями
- •5. Размещения данного состава
- •2. Бином Ньютона
- •3. Формула разложения разности n-ых степеней
- •4. Метод математической индукции
- •5. Формула Тейлора
- •Упражнения к § 3.1 Комбинаторика
- •§ 3.2. Комплексные числа
- •1. Алгебраическая форма комплексного числа
- •2. Геометрическое представление, тригонометрическая и показательная формы комплексного числа
- •3. Действия над комплексными числами в тригонометрической и показательной формах
- •Упражнения к § 3.2
- •Глава 4 Индивидуальные домашние задания
- •§ 4.1. Индивидуальное домашнее задание (идз) по теме: “Предел функции и непрерывность”
- •§ 4. 2. Индивидуальное домашнее задание по теме: «Производная и ее применение»
- •Глава 6 Семинарские занятия
- •§ 6.1. Cеминар: Применение производной при исследовании функции
- •Задания для семинара
- •Задания для самостоятельной работы
- •§ 6.2. Семинар: Неопределенный интеграл
- •Задания для семинара
- •Задания для самостоятельной работы
- •Ответы Ответы к гл. 3
- •Ответы к идз: Пределы и нелрерывность
- •Литература
3. Действия над комплексными числами в тригонометрической и показательной формах
Умножение. Модуль произведения равен произведению модулей, аргумент произведения равен сумме аргументов:
 (2.16)
(2.16)
Деление. Модуль частного равен частному модулей, аргумент частного равен разности аргументов:
 (2.17)
(2.17)
Возведение в целую степень п. Модуль возводится в степень п, аргумент умножается на п.
![]() (2.18)
(2.18)
Извлечение
корня степени п.
Извлекается арифметический корень из
модуля, общее значение аргумента делится
на п. Корень
имеет ровно п
различных
значений, если
![]()
![]() (2.19)
(2.19)
![]()
Формулы (2.18) и (2.19) называются формулами Муавра.
Упражнения к § 3.2
3.20. Выполнить действия
-

-

-

-
 ;
5)
;
5)
 ;
6)
;
6)
 ;
7)
;
7)
 ;
;
-
 9)
9)
 .
.
3.21. Представить в виде суммы более простых дробей:
1)
![]() ;
2)
;
2)
![]() ;
3)
;
3)
![]() .
.
3.22. Решить уравнения:
1)
![]() ,
2)
,
2)
![]() ,
,
3)
![]() ,
4)
,
4)
![]() ,
5)
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() ,
8)
,
8)
![]() ,
9)
,
9)
![]() ,
10)
,
10)
![]() ,
,
11)
![]() .
.
3.23. Построить на комплексной плоскости и представить в тригонометрической форме числа:
1)
![]() , 2)
, 2)
![]() ,
3)
,
3)
![]() ,
4)
,
4)
![]() ,
,
5)
![]() ,
6)
,
6)
![]() ,
7)
,
7)
![]() ,
8)
,
8)
![]() ,
,
9) 5, 10) i.
3.24. Представить в показательной форме числа (указать главное значение аргумента ):
-
 2)
2)
 ;
;
3)
![]() 4)
4)
![]() ;
;
5)
![]() 6)
6)
![]()
7)
![]() 8)
8)
![]() 9)
9)
![]()
10)
![]()
11)
![]() 12)
12)
![]()
13)
![]() 14)
14)
![]()
3.25.
Выполнить действия: 1)
![]() 2)
2)
![]() ,
,
3)
![]() ,
4)
,
4)
![]() ,
5)
,
5)
![]() ,
,
6)
![]() ,
7)
,
7)
![]() ,
8)
,
8)
![]()
9)
![]() ,
10)
,
10)
![]() ,
,
11)
![]() , 12)
, 12)
![]() ,
13)
,
13)
![]() ,
,
14)
![]() ,
15)
,
15)
![]() 16)
16)
![]() 17)
17)
![]() .
.
3.26.
Найти все значения корней:

![]()
3.27.
Решить уравнения:
![]()
![]()
3.28.
Выразить через степени![]() и
и![]() следующие
функции:
следующие
функции:
![]()
3.29. Доказать:
1)

2)

3)
![]()
![]()
 если
если
![]() .
.
Указание. Воспользуйтесь формулами Эйлера

а также формулой суммы членов геометрической прогрессии.
Глава 4 Индивидуальные домашние задания
§ 4.1. Индивидуальное домашнее задание (идз) по теме: “Предел функции и непрерывность”
Задача 1. Найти пределы:
|
1.1.
|
1.2.
|
|
1.3.
|
1.4.
|
|
1.5.
|
1.6.
|
|
1.7.
|
1.8.
|
|
1.9.
|
1.10
|
|
1.11
|
1.12.
|
|
1.13.
|
1.14.
|
|
1.15.
|
1.16.
|
|
1.17.
|
1.18.
|
|
1.19.
|
1.20.
|
|
1.21.
|
1.22.
|
|
1.23.
|
1.24.
|
|
1.25.
|
1.26.
|
|
1.27.
|
1.28.
|
|
1.29.
|
1.30.
|
Задача 2. Найти пределы.
|
2.1.
|
2.2.
|
|||
|
2.3.
|
2.4.
|
|||
|
2.5.
|
2.6.
|
|||
|
2.7.
|
2.8.
|
|||
|
2.9.
|
2.10.
|
|||
|
2.11.
|
|
|||
|
2.13.
|
|
|||
|
2.14.
|
|
|||
|
2.15.
|
|
|||
|
2.16.
|
|
|||
|
2.17.
|
|
|||
|
2.18.
|
|
|||
|
2.19.
|
|
|||
|
2.20.
2.21.
|
|
|||
|
2.22.
|
|
|||
|
2.23.
|
|
|||
|
2.25.
|
|
|||
|
2.26.
2.27.
|
|
|||
|
2.28.
|
|
|||
|
2.29.
|
|
|||
|
2.30.
|
|
|||
Задача 3. Доказать непрерывность функции f(x) в точке x0.
|
3.1. f(x)=6-x2, x0=2 |
3.2. f(x)=3x2-2, x0=-2 |
|
3.3. f(x)=-2x2-3, x0=3 |
3.4. f(x)=2x2+5, x0=-3 |
|
3.5. f(x)=5x2-1, x0=4 |
3.6. f(x)=2-3x2, x0=4 |
|
3.7. f(x)=4x2-3, x0=-1 |
3.8. f(x)=4x2+5, x0=2 |
|
3.9. f(x)=x2+7, x0=-3 |
3.10. f(x)=7-2x2, x0=3 |
|
3.11. f(x)=-2x2-7, x0=2 |
3.12. f(x)=3x2+2, x0=4 |
|
3.13. f (x)=5x2+3, x0=-2 |
3.14. f(x)=4x2-1, x0=-3 |
|
3.15. f(x)=7x2-1, x0=4 |
3.16. f(x)=-8x2-1, x0=1 |
|
3.17. f(x)=2x2+11, x0=5 |
3.18. f(x)=10x2-3, x0=5 |
|
3.19. f(x)=13-2x2, x0=3 |
3.20. f(x)=3-10x2, x0=4 |
|
3.21. f(x)=4x2-11, x0=-2 |
3.22. f(x)=1-5x2, x0=2 |
|
3.23. f(x)=3-4x2, x0=1 |
3.24. f(x)=-7-x2, x0=1 |
|
3.25. f(x)=x2-6, x0=3 |
3.26. f(x)=9-5x2, x0=-2 |
|
3.27. f(x)=7-5x2, x0=-2 |
3.28. f(x)=-2x2-1, x0=3 |
|
3.29. f(x)=11-3x2, x0=2 |
3.30. f(x)=4x2-15, x0=-1 |
Задача 4. Найти пределы разложением на множители и по правилу Лопиталя.
|
4.1.
|
4.2.
|
|
4.3.
|
4.4.
|
|
4.5.
|
4.6.
|
|
4.7.
|
4.8.
|
|
4.9.
|
4.10.
|
|
4.11.
|
4.12.
|
|
4.13.
|
4.14.
|
|
4.15.
|
4.16.
|
|
4.17.
|
4.18.
|
|
4.19.
|
4.20.
|
|
4.21.
|
4.22.
|
|
4.23.
|
4.24.
|
|
4.25.
|
4.26.
|
|
4.27.
|
4.28.
|
|
4.29.
|
4.30.
|
Задача 5. Найти пределы, используя метод освобождения от иррациональности.
|
5.1.
|
5.2.
|
|
|
5.3.
|
5.4.
|
|
|
5.5.
|
5.6.
|
|
|
5.7.
|
5.8.
|
|
|
5.9.
|
5.10.
|
|
|
5.11.
|
5.12.
|
|
|
5.13.
|
5.14.
|
|
|
5.15.
|
5.16.
|
|
|
5.17.
|
5.18.
|
|
|
5.19.
|
5.20.
|
|
|
5.21.
|
|
|
|
5.22.
|
5.23.
|
|
|
5.24.
|
5.25.
|
|
|
5.26.
|
5.27.
|
|
|
5.28.
|
5.29.
|
|
|
5.30.
|
|
|
Задача 6. Найти пределы, используя эквивалентные бесконечно-малые.
|
6.1.
|
6.2.
|
|
6.3.
|
6.4.
|
|
6.5.
|
6.6.
|
|
6.7.
|
6.8.
|
|
6.9.
|
6.10.
|
|
6.11.
|
6.12.
|
|
6.13.
|
6.14.
|
|
6.15.
|
6.16.
|
|
6.17.
|
6.18.
|
|
6.19.
|
6.20.
|
|
6.21.
|
6.22.
|
|
6.23.
|
6.24.
|
|
6.25.
|
6.26.
|
|
6.27.
|
6.28.
|
|
6.29.
|
6.30.
|
Задача 7. Найти пределы, используя эквивалентные бесконечно малые.
|
7.1.
|
7.2.
|
|
7.3.
|
7.4.
|
|
7.5.
|
7.6.
|
|
7.7.
|
7.8.
|
|
7.9.
|
7.10.
|
|
7.11. |
7.12.
|
|
7.13.
|
7.14.
|
|
7.15.
|
7.16.
|
|
7.17.
|
7.18.
|
|
7.19.
|
7.20.
|
|
7.21.
|
7.22.
|
|
7.23.
|
7.24.
|
|
7.25.
|
7.26.
|
|
7.27.
|
7.28.
|
|
7.29.
|
7.30.
|
Задача 8. Найти пределы, используя эквивалентные бесконечно малые.
|
8.1.
|
8.2.
|
|
8.3.
|
8.4.
|
|
8.5.
|
8.6.
|
|
8.7.
|
8.8.
|
|
8.9.
|
8.10.
|
|
8.11.
|
8.12.
|
|
8.13.
|
8.14.
|
|
8.15.
|
8.16.
|
|
8.17.
|
8.18.
|
|
8.19.
|
8.20.
|
|
8.21.
|
8.22.
|
|
8.23.
|
8.24.
|
|
8.25.
|
8.26.
|
|
8.27.
|
8.28.
|
|
8.29.
|
8.30.
|
Задача 9. Используя формулы второго замечательного предела и его следствий, найти пределы функций.
|
9.1.
|
9.2.
|
|
9.3.
|
9.4.
|
|
9.5.
|
9.6.
|
|
9.7.
|
9.8.
|
|
9.9.
|
9.10.
|
|
9.11
|
9.12.
|
|
9.13.
|
9.14.
|
|
9.15.
|
9.16.
|
|
9.17.
|
9.18.
|
|
9.19.
|
9.20.
|
|
9.21.
|
9.22.
|
|
9.23.
|
9.24.
|
|
9.25.
|
9.26.
|
|
9.27.
|
9.28.
|
|
9.29.
|
9.30.
|
Задача 10. Используя правило Лопиталя и эквивалентность, найти следующие пределы.
|
10.1.
a)
|
б)
|
|
10.2.
а)
|
б)
|
|
10.3.
а)
|
б)
|
|
10.4.
а)
|
б)
|
|
10.5.
а)
|
б)
|
|
10.6.
а)
|
б)
|
|
10.7.
а)
|
б)
|
|
10.8.
а)
|
б)
|
|
10.9.
а)
|
б)
|
|
10.10.
а)
|
б)
|
|
10.11.
а)
|
б)
|
|
10.12.
а)
|
б)
|
|
10.13.
|
б)
|
|
10.14.
|
б)
|
|
10.15.
а)
|
б)
|
|
10.16.
а)
|
б)
|
|
10.17.
а)
|
б)
|
|
10.18.
а)
|
б)
|
|
10.19.
а)
|
б)
|
|
10.20.
а)
|
б)
|
|
10.21.
а)
|
б)
|
|
10.22.
а)
|
б)
|
|
10.23.
а)
|
б)
|
|
10.24.
а)
|
б)
|
|
10.25.
а)
|
б)
|
|
10.26.
а)
|
б)
|
|
10.27.
а)
|
б)
|
|
10.28.
а)
|
б)
|
|
10.29.
|
б)
|
|
10.30.
|
б)
|
Задача 11. Применяя формулу Тейлора, вычислить пределы.
|
11.1
|
11.2.
|
|
|
11.3.
|
11.4.
|
|
|
11.5.
|
11.6.
|
|
|
11.7.
|
11.8.
|
|
|
11.9.
|
11.10.
|
|
|
11.11.
|
11.12.
|
|
|
11.13.
|
11.14.
|
|
|
11.15.
|
11.16.
|
|
|
11.17.
|
11.18.
|
|
|
11.19.
|
11.20
|
|
|
11.21.
|
11.22.
|
|
|
11.23.
|
11.24.
|
|
|
11.25.
|
11.26.
|
|
|
11.27.
|
11.28.
|
|
|
11.29.
|
11.30.
|
|
Задача 12. Найти точки разрыва, уравнения асимптот и построить схематично график функции.
|
12.1.
а)
|
б)
|
|
|
|
12.2.
а)
|
б)
|
|
|
|
12.3.
а)
|
б)
|
|
|
|
12.4.
а)
|
б)
|
|
|
|
12.5.
а)
|
б)
|
|
|
|
12.6.
а)
|
б)
|
|
|
|
12.7.
а)
|
б)
|
|
|
|
12.8.
а)
|
б)
|
||
|
12.9.
а)
|
б)
|
||
|
12.10.
а)
|
б)
|
||
|
12.11.
а)
|
б)
|
||
|
12.12.
а)
|
б)
|
||
|
12.13.
а)
|
б)
|
||
|
12.14.
а)
|
б)
|
||
|
12.15.
а)
|
б)
|
||
|
12.16.
а)
|
б)
|
||
|
12.17.
а)
|
б)
|
||
|
12.18.
а)
|
б)
|
||
|
12.19.
а)
|
б)
|
||
|
12.20
.а)
|
б)
|
||
|
12.21.
а)
|
б)
|
||
|
12.22.
а)
|
б)
|
||
|
12.23.
а)
|
б)
|
||
|
12.24.
а)
|
б)
|
||
|
12.25.
а)
|
б)
|
||
|
12.26.
а)
|
б)
|
||
|
12.27.
а)
|
б)
|
||
|
12.28.
а)
|
б)
|
||
|
12.29.
а)
|
б)
|
||
|
12.30.
а)
|
б)
|
||












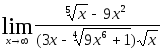













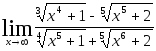
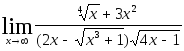

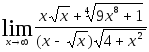








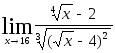


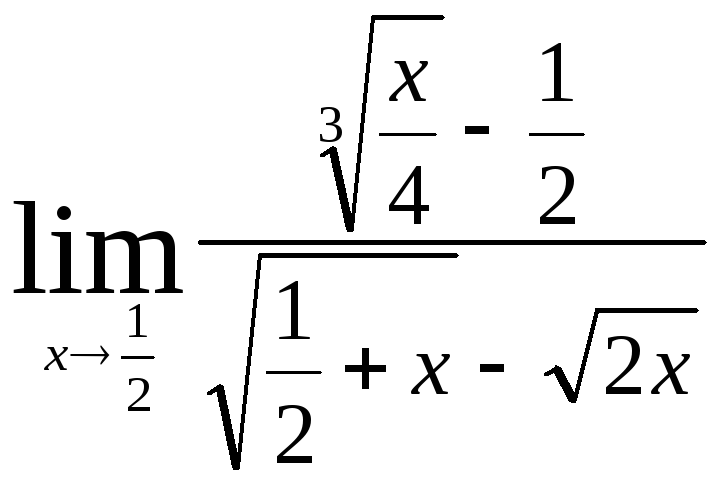




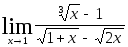


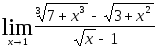


















































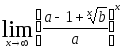 (a,
b>0)
(a,
b>0)