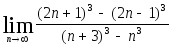- •Содержание
- •Предисловие
- •Глава 1. Элементы аналитической геометрии и линейной алгебры
- •§1. Семинарские занятия Семинар №1
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •Семинар №2 Точка и прямая на плоскости. Окружность.
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •Семинар № 3 Кривые второго порядка.
- •Задачи для решения на семинаре
- •Семинар № 4 Векторная алгебра.
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •Семинар № 5 Прямая и плоскость в пространстве
- •Задачи для решения на семинаре
- •Семинар № 6 Матрицы. Действия над матрицами.
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •Семинар № 7 Ранг матрицы. Системы линейных уравнений.
- •Задачи для решения на семинаре
- •Задачи для самостоятельной работы
- •§ 2. Примерное содержание рейтинговых контрольных работ в первом семестре
- •§ 3. Методы построения графиков функций Графики некоторых функций
- •Некоторые функции, примыкающие к элементарным
- •Глава 2. Предел функции. Непрерывность
- •§ 2.1. Предел числовой последовательности
- •1.1. Определение числовой последовательности
- •1.2. Предел числовой последовательности
- •1.3. Свойства передела
- •Упражнения к § 2.1
- •§ 2.2. Предел функции. Методы вычисления предела
- •1. Определение предела функции
- •2. Свойства предела функции
- •3. Методы вычисления предела функции
- •5. Неопределенность .
- •Упражнения к § 2.2
- •§ 2.3. Эквивалентные бесконечно малые. Применение эквивалентности при вычислении пределов
- •§2.4. Непрерывность. Точки разрыва. График функции
- •2. Понятие о точках разрыва и их классификация
- •2) Точки разрыва 1-го рода (конечный разрыв)
- •3) Точки разрыва 2-го рода (бесконечный разрыв)
- •3. Об асимптотах графика функции
- •§ 2.5. Производная. Дифференцирование функций
- •1. Производные функций, заданных явно
- •Упражнения к § 2.5
- •2. Производные высших порядков явных функций
- •3. Производные функций, заданных параметрически
- •4. Производные функций, заданных неявно
- •§ 2.6. Вычисление пределов с помощью правила Лопиталя
- •1. Неопределенности и .
- •2. Другие неопределенности
- •Упражнения к § 2.6
- •§ 2.7. Применение формулы Тейлора при вычислении предела функции
- •Упражнения к § 2.7
- •Ответы к главе 2
- •Литература
Глава 2. Предел функции. Непрерывность
§ 2.1. Предел числовой последовательности
1.1. Определение числовой последовательности
Числовой
последовательностью называется
бесконечное множество чисел (элементов),
имеющих определенные номера. Эти числа
являются членами последовательности:
x1
![]() первый
член, x2
первый
член, x2![]() второй
член, ... , xn
второй
член, ... , xn
![]() n-ый
член. Числовая последовательность
обозначается так: {xn}.
n-ый
член. Числовая последовательность
обозначается так: {xn}.
Числовую
последовательность задают формулой
n-го
члена: xn=f(n).
Например, если
![]()
то
x1=2,
![]()
![]() ,
...,
,
...,
![]() и т.д.
и т.д.
Числовую
последовательность также можно задать
рекуррентным соотношением:
![]() ,
x1=1.
,
x1=1.
Тогда
![]() ,
,![]() ,
,![]() и т.д.
и т.д.
1.2. Предел числовой последовательности
Определение.
Число а
называется пределом числовой
последовательности {xn},
если для
![]() такое, что для всех n>N
выполняется условие
такое, что для всех n>N
выполняется условие
![]() .
.
Это означает, что в любой окрестности точки а содержится бесконечное множество элементов последовательности.
![]() :
:
![]()
Доказать,
что
![]() означает найти зависимость
означает найти зависимость
![]()
Числовая
последовательность, имеющая предел,
называется сходящейся. Если же предел
не существует или равен
![]() ,
то последовательность называется
расходящейся.
,
то последовательность называется
расходящейся.
1.3. Свойства передела
1. Предел линейной комбинации
![]() .
.
2.
Предел произведения
![]() .
.
3.
Предел частного  ,
если
,
если
![]() .
.
4. Предел отношения многочленов.
Если
![]() и
и
![]() многочлены от n
степени k
и m
соответственно, т.е.
многочлены от n
степени k
и m
соответственно, т.е.
![]()
![]() то
предел отношения многочленов равен
пределу отношения их старших членов:
то
предел отношения многочленов равен
пределу отношения их старших членов:
![]()
Упражнения к § 2.1
Найти пределы:
|
2.1.
|
2.2. |
||
|
2.3.
|
2.4.
|
||
|
2.5.
|
2.6.
|
||
|
2.7.
|
|
||
|
2.8.
|
|
||
|
2.9.
|
|
||
|
|
|
||
|
2.11.
|
2.12.
|
||
|
|
|
||
|
2.15.
|
|
||
|
2.18. |
|
||
|
2.19.
2.20.
|
|
||
|
2.21.
|
|
||
|
2.22.
|
|
||
|
2.23.
|
2.24.
|
||
|
|
|
||
|
2.25.
|
|
||
|
2.26.
|
|
||
|
2.27.
|
|
||
|
|
|
||
|
2.29.
|
2.30.
|
||
|
|
|
||
|
2.31.
|
2.32.
|
||
|
2.33.
|
|
||
|
2.34.
|
|
||
|
2.35.
|
2.36.
|
||
|
2.37.
|
2.38.
|
||
|
2.39.
|
2.40.
|
||
|
2.41.
|
2.42.
|
||
|
2.43.
|
2.44.
|
||
|
2.45.
|
2.46.
|
||
|
2.47.
|
2.48.*
|
||
2.49.*
![]()
2.50.*
![]()
2.51.*
![]()
2.52.*
![]()
Доказать
(найти зависимость
![]()
2.53.
![]() 2.54.
2.54.
![]()
2.55.
![]() 2.56.
2.56.
![]()
2.57.
![]()
Найти пределы последовательностей, заданных рекуррентными соотношениями.
2.58.
![]() ,
где
n
=
1,
2, ...
,
где
n
=
1,
2, ...
2.59.
![]() ,
,
![]()
2.60.
![]() , где (a>0).
, где (a>0).