Семинар № 6 Матрицы. Действия над матрицами.
1. Матрицы. Прямоугольные и квадратные, диагональные и единичные. Транспонирование матриц.
2. Умножение матрицы на число. Сложение матриц.
3. Умножение матриц.
4. Обратная матрица.
5. Решение матричных уравнений.
Задачи для решения на семинаре
№1.
Найти матрицу Х
из матричного
уравнения
,
если
,
.
№2.
Даны матрицы
.
Найти:
1) АВ, 2)
АС, 3)
ВС,
4) ВЕ,
Е
единичная
матрица.
№3.
Даны матрицы
.
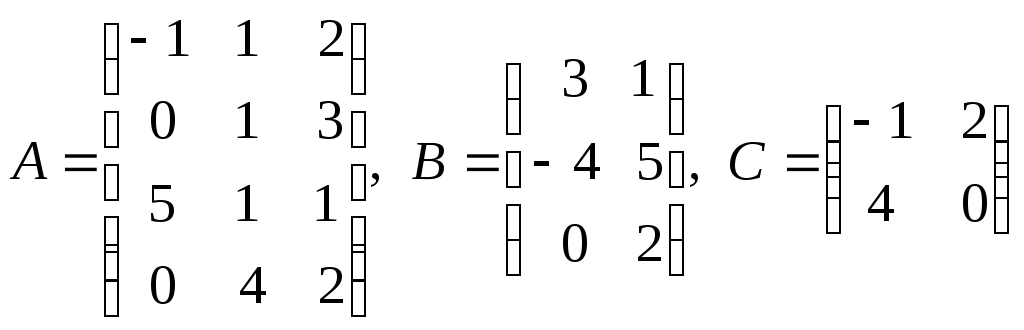Найти
.
В ответе записать транспонированную
матрицу.
№4. Найти обратную матрицу:
1)
,
2)
.
№5. Решить матричные уравнения:
1)
,
если
;
2)
,
если
.
Задачи для самостоятельной работы
№6.
Найти матрицу Х
из матричного
уравнения
,
если
,
.
№7.
Даны матрицы
.
Найти:
1) АВ, 2)
АС, 3)
ВС,
4) ВЕ,
Е
единичная матрица.
№8.
Даны матрицы
.
Найти
.
В ответе записать транспонированную
матрицу.
№9. Найти обратную матрицу:
1)
,
2)
.
№10. Решить матричные уравнения:
1)
,
если
;
2)
,
если
.
Семинар № 7 Ранг матрицы. Системы линейных уравнений.
1. Ранг матрицы. Методы нахождения ранга.
2. Условие совместности системы линейных неоднородных уравнений.
3. Случай определенного решения. (Методы Крамера и Гаусса повторить). Матричный способ решения системы.
4. Случай неопределенного решения. Нахождение общего решения неоднородной системы.
5. Нахождение фундаментальной системы решений для системы линейных однородных уравнений.
Задачи для решения на семинаре
№1. Найти ранг матрицы:
а)
,
б)
,
в)
№2
. 1) Когда ранг матрицы
равен п?
2) Когда система п
векторов
линейно независима?
№3. С помощью ранга матрицы исследовать на линейную независимость систему векторов:
1)
;
2)
.
№4. Проверить системы линейных уравнений на совместность.
Совместные системы решить по правилу Крамера, методом Гаусса и методом Жордана.
1)
,
2)
.
№5. Найти общее решение системы неоднородных уравнений
.
№6. Найти фундаментальную систему решений (ФСР) системы однородных уравнений
.
Задачи для самостоятельной работы
№7. Найти ранг матрицы:
а)
,
б)
,
в)
.
№8. С помощью ранга матрицы исследовать на линейную независимость систему векторов:
1)
;
2)
.
№9. Проверить системы линейных уравнений на совместность. Совместные системы решить по правилу Крамера, методом Гаусса и методом Жордана.
1)
,
2)
.
№10. Найти общее решение системы неоднородных уравнений
.
№11. Найти фундаментальную систему решений (ФСР) системы однородных уравнений
.
§ 2. Примерное содержание рейтинговых контрольных работ в первом семестре
Контрольная работа №1 по теме: «Элементы аналитической геометрии и линейной алгебры»
Вариант № 0
1.
Даны вершины треугольника
,
.
Через середину АВ
проведен перпендикуляр к АВ.
Найти точку пересечения его со стороной
ВС.
2.
Найти координаты центра, полуоси, фокусы,
директрисы гиперболы
.
3.
Даны векторы
.
Найти
векторное произведение
.
4.
Составить уравнение плоскости, проходящей
через две параллельные прямые
и
.
5. Решить матричное уравнение
,
если
.
6. Проверить систему линейных уравнений на совместность.
Решить методом Жордана
7. Найти общее решение системы неоднородных уравнений
Контрольная работа №2 по теме: « Предел. Непрерывность»
Вариант № 0
Найти пределы:
1.
.
2.
.
3.
.
4.
.
5.
.
6.
Сравнить
бесконечно малые:
7. Построить график функции (указать точки разрыва):
а)
б)
.
Контрольная работа № 3 по теме: «Производная»
Вариант № 0
Найти первую производную функций (1-3)
1.
.
2.
.
3.
.
4.
Найти первую
и вторую производную функции, заданной
параметрически
.
5.
Найти первую
и вторую производную неявной функции 
.
6.
Для функции
по формуле Лейбница найти
.
7.
Для функции
найти
.