Упражнения к § 2.7
Используя формулу Тейлора, найти пределы.
|
2.318.
|
2.319.
|
|
2.320.
|
2.321.
|
|
2.322.
|
2.323.
|
|
2.324.
|
2.325.
|
|
2.326.
|
2.327.
|
|
2.328.
|
2.329.
|
|
2.330.
|
2.331.
|
Ответы
Ответы к гл. 1
Семинар №1
1.
a) 31 , b)
0 , c)
,
d) 4, -5. 2.
a)
38, b)
-16, c) 0,
d) 0,
e) 24, f
)368. 3. a)
- 85 , b)
27. 4. a)
,
b)
5.
.
6. a)
-26 , b)
0 , c)
,
d) 2, -3.
7. a) 55, b) 44 , c) 0, d )0, e) -90, f ) -48. 8. a) -16 , b) – 848.
9. a)
,
b)
.
10.
Семинар №2
1.
2. а)
; б)
3.
4.
1) 10, 2)
,
4)
5)
5.
а)
,
б)
,
в)
.
6.
.
7.
.
8.
9.
10. а)
; б)
11.
.
12.
а)
,
б)
,
в)
.
13.
14.
15.
Семинар №3
1.
.
2.
.
3.
.
4.
,
.
5.
.
6.
.
7.
.
8.
9.
10.
.
11.
.
12.
,
.
13.
.
14.
.
15.
16.
Семинар №4
1.
.
2.
,
.
3.
6 или -6. 4.
5.
6.
или
.
7.
.
8. Х = -1, У = 1.
9. 1) 13, 2) 5. 10.
10. 11. 1)
,
2) 14.
12.
.
13. 1) компланарные, 2) левая тройка. 14. 3.
15. 1) нет, 2) да.
Семинар №5
1.
1)
,
2)
3. 1)
,
2)
,
3)
.
4.
.
5.
6.
или
.
7.
.
8. 2. 9. 11.
10. 1)
,
2)
,
3)
11. 1)
,
2) параллельны.
12.
.
13
.
Семинар №6
1.
.
2.
1)
,
2)
,
3)
,
4)
.
3.
.
4.1)
,
2)
.
5.
1)
2)
.
6.
.
7.
1)
,
2)
,
3)
,
4)
.
8.
.
9. 1)
,
2)
.
10. 1)
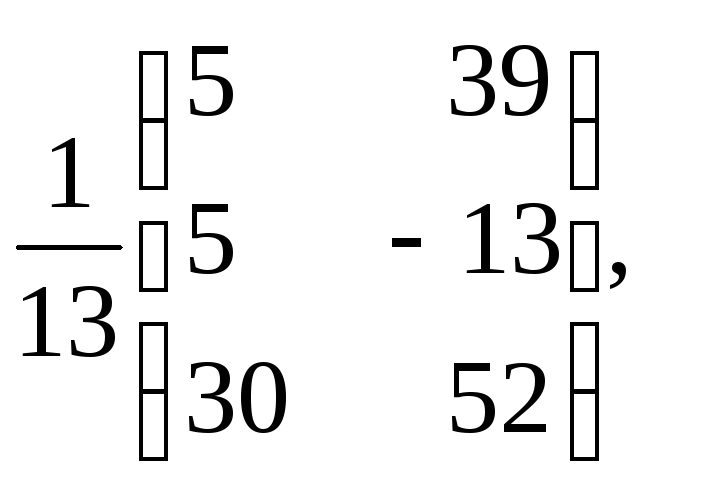2)
.
Семинар№7
1. а) 2, б) 2, в) 3.
2. 1) если определитель матрицы не равен нулю, 2) если ранг матрицы, составленный из координат векторов равен п .
3.
1) линейно
зависимая
,
2) линейно независимы.
4.
1)
,
2) система не совместна.
5.
.
6.
Если свободные
переменные
,
то ФСР имеет вид:
Общее
решение
.
7. а )2, б) 3, в) 2.
8.
1) линейно
независимы., 2)линейно зависимая
9.
1) система
не совместна, 2)
.
10.
.
11.
Если свободные
переменные
,
то ФСР имеет вид:
Общее
решение
.
Ответы к главе 2
2.1.
2/3,
2.2.
24/9, 2.3.
,
2.4.
0, 2.5.
0, 2.6.
,
2.7.
17/30,
2.8.
13/8,
2.9.
1/4, 2.10.
-1/2 2.11.
.
2.12.
0, 2.13.
3/2,
2.14.
2,
2.15.
4/3, 2.16.
4/3, 2.17.
0, 2.18.
1,
2.19.
5/7,
2.20.
9/5,
2.21.
5/3, 2.22. 5/4,
2.23.
,
2.24.
,
2.25.
16/3, 2.26.
9/2, 2.27.
20,
2.28.
-1/25, 2.29.
1, 2.30.
1/3, 2.31.
1,
2.32.
1,
2.33.
1, 2.34.
3, 2.35.
5/4, 2.36.
20/9, 2.37. 3/4,
2.38.
7/2, 2.39.
3/2, 2.40.
,
2.41.
5/2,
2.42.
0, 2.43.1/2,
2.44.
,
2.45.
1, 2.46.
1/4,
2.47.
2/3, 2.48.
2, 2.49.
23/90, 2.50.
1/4,
2.51.
1/8, 2.52.
/4,
2.53.
,
2.54.
,
2.55.
,
2.56.
,
если
;
если же
,
то N=0;
2.57.
,
2.58.
,
2.59.
,
2.60.
,
2.61.
-8/5, 2.62.
0.2,
2.63.
0,
2.64.
0, 2.65.
,
2.66.
,
2.67.
0,
2.68.
0, 2.69.
8/3,
2.70.
2, 2.71.
,
2.72.
0, 2.73.
1/2, 2.74.
1/4,
2.75.
,
2.76.
0, 2.77.
400,
2.78.
145/1024,
2.79.
49/24, 2.80.
n(n+1)/2,
2.81.
m/n,
2.82.
19/9, 2.83.
21, 2.84.
n(n+1)/2,
2.85.
1/2, 2.86.
1/24,
2.87.
12/5,
2.88.
3/4,
2.89.
144,
2.90,
-2, 2.91.
2/3,
2.92.
,
2.93.
1/4,
2.94.
1/2, 2.95.
1/12,
2.96.
20, 2.97.
0, 2.98.
,
2.99.
e-5,
2.100.
e-0.3,
2.101.
e3,
2.102.
e-6,
2.103.
e6,
2.104.
e8/3,
2.105.
,
2.106.
16, 2.107.
e4,
2.108.
e6/5,
2.109.
0, 2.110.
,
2.111.
-2.5,
2.112. 1/6, 2.113. 200,
2.114.
,
2.115.
,
2.116.
,
2.117.
1,
2.118.
6, 2.119.
,
2.120.
3, 2.121.
2, 2.122.
,
2.123.
-6/
,
2.124.
11/8
,
2.125
,
2.126.
3/2,
2.127.
,
2.128.
6,
2.129.
2,
2.130.
1/5, 2.131.
2/
,
2.132.
5/4, 2.133.
65/112, 2.134.
7/36, 2.135.
1/48,
2.136.
29, 2.137.
1, 2.138.
2/
,
2.139.
а/
,2.140.
1/2, 2.141.
sina,
2.142.
,
2.143.
3/11e,
2.144.
2a2lna,
2.145.
,
2.146.
-1/8, 2.147.
8, 2.148.
a/cos2a,
2.149.
9ln3/
,
2.150.
3ln3, 2.151.
,
2.152.
1/8, 2.153.
,
2.154.
30.1,
2.155.
,
2.156.
,
2.157.
e-1,
2.158.
e3/2,
2.159.
,
2.160.
,
2.161.
axln2a,
2.162.
e-(a+b),
2.163.
lna,
2.164.
6, 2.165.
,
2.166.
ablna,
2.167.
,
2.168.
e,
2.169.
,
2.170.
-1/2, 2.171.
sinx/x,
2.172.
0, 2.173.
½,
2.174. 1/2, 2.175. одного порядка, 2.175(а). не сравнимы.
2.177.
при
,
2.178. а)
1/3; б) 1/2; в) эквивалентны; г) 2; д) 2; е)
эквивалентны, 2.179.
1) 1.03; 2) 3.167; 3) 26/9 = 2.(8); 4) 1.12; 5) 0.72; 6) 0.043,
2.180. Указание. Произвести замену x = t20.
2.181.
точки бесконечного разрыва,
x=2
и x
=
2
вертикальные асимптоты,
y=0
горизонтальная асимптота.
2
.182.
-
точки бесконечного разрыва, x
=
1
и x
= 1
вертикальные
односторонние асимптоты,
y
=1
горизонтальная
асимптота..
2.183.
x
=1
точка бесконечного разрыва,
x
=1
вертикальная (правосторонняя)
асимптота,
y
=1
горизонтальная
асимптота.
2
.184.
х = 3
точка разрыва 1-го рода,
у
= 0
горизонтальная асимптота.
2.185.
,
горизонтальная
асимптота.
2.186.
-
точки бесконечного разрыва,
x
=2 и x
=
2
вертикальные асимптоты,
y
=1
горизонтальная асимптота..
2
.187.
- точки разрыва 2-го рода,
x
=
3
и x
= 3
вертикальные
односторонние асимптоты,
y
=1
горизонтальная асимптота.
2
.188.
точки разрыва 2-го рода,
x
=
1
и x
=1 – вертикальные
односторонние асимптоты,
y
=1
горизонтальная асимптота.
2
.189.
x
= 2
точка разрыва 2-го рода,
x
=2
вертикальная левосторонняя
асимптота,
y
=1
горизонтальная
асимптота.
2
.190.
точки разрыва 2-го рода,
x
=
2
и x
= 2
вертикальные
левосторонние асимптоты,
y=1
горизонтальная асимптота.
2.191.
x
= 1
точка конечного разрыва,
скачок
,
горизонтальная
а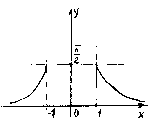
симптота,
.
2.192.
,
y
=0
горизонтальная
асимптота.
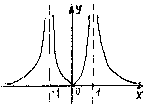
2.193.
x
= 0
точка устранимого разрыва,
точка
разрыва 2-го рода,
x
=
1
и x
=1
вертикальные асимптоты,
y
= 0
горизонтальная асимптота..
2
.194.
x
= 0
точка устранимого разрыва,
горизонтальная
асимптота,
.
2
.195.
x
= 0
точка конечного разрыва,
h(0)=
1,
горизонтальная
асимптота,
0<y<1.
2.196.
x
=1
точка разрыва 1-го рода,
скачок
h(1)
=1,
-
горизонтальная асимптота,
0<y<1.
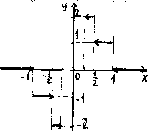
2.197.
x
= 0
точка бесконечного разрыва,
точки
разрыва 1-го рода..
2
.198.
x
= k2
точки
разрыва 1-го рода..
2.199.
точки
разрыва 1-го рода.
2
.200.
x
=
1
точка
устранимого разрыва,
x
= 0
точка разрыва 2-го рода.
2
.201.
точка конечного разрыва,
скачок
.
2
.202.
x
= 0
точка бесконечного разрыва,
скачок
h(1)
=
2,
y
= 0
горизонтальная асимптота..
2
.203.
x
=
1
точка разрыва 1-го рода,
скачок
h(
1)=-3,
x
= 0
точка разрыва 2-го рода,
y
= 0
правосторонняя
горизонтальная асимптота,
x
= 0
вертикальная асимптота.
2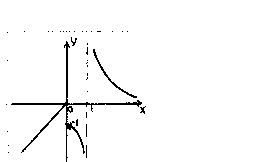
.204.
x
= 0
точка разрыва 1-го рода,
скачок
h(0)=
1,
x
=1
точка разрыва 2-го рода,
x
= 0
горизонтальная асимптота.
2
.205.
x
= 1
точка разрыва 2-го рода,
x
= 1
вертикальная
двусторонняя асимптота,
– наклонная
двусторонняя асимптота.
2.206. х = 0 – точка устранимого
разрыва; у = х – двусторонняя
наклонная асимптота.
2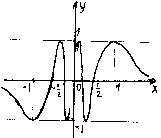
.207.
х =
0
точка разрыва 2-го рода,
график пересекает ось Ox
в
интервале
бесконечное
число
раз в точках
,
у
=0
горизонтальная асимптота..
2
.208.
x
=
1
точка бесконечного разрыва,
x=
1
вертикальная двусторонняя
асимптота,
y
= x
+1
наклонная
асимптота.
2
.209.
В точках
разрыв 1-го рода..
2
.210.
x
= 1
точка бесконечного разрыва,
x
=1
вертикальная двусторонняя
асимптота,
y
=0
горизонтальная
правосторонняя асимптота.
2.211.
x
= 0
точка
устранимого разрыва,
.
2.212.
x
= 0
точка устранимого разрыва,
.
2.213.
x
= 0
точка устранимого разрыва, f(0)=2;
точки разрыва 2-го рода. 2.214.
x
= 0
точка
устранимого разрыва, f(0)
=
1,
x
=1
точка устранимого разрыва, f(1)=0;
x=
1
точка разрыва 2-го рода. 2.215.
x
=
1
точка устранимого разрыва, f(
1)=1.
2.216.
x=0
точка устранимого разрыва, f(0)=1/2.
2.217. x=1
точка устранимого разрыва, f(1)=e3.
2.219.
точки устранимого разрыва,
;
точки разрыва 1-го рода, скачок
,
.
2.220.
x
=2
точка устранимого разрыва, f(2)=1.
2.221.
,
2.222.
a=2,
2.223.
2.224.
2.225.
a=3,
,
2.226.
2.228.
a)
,
б)
,
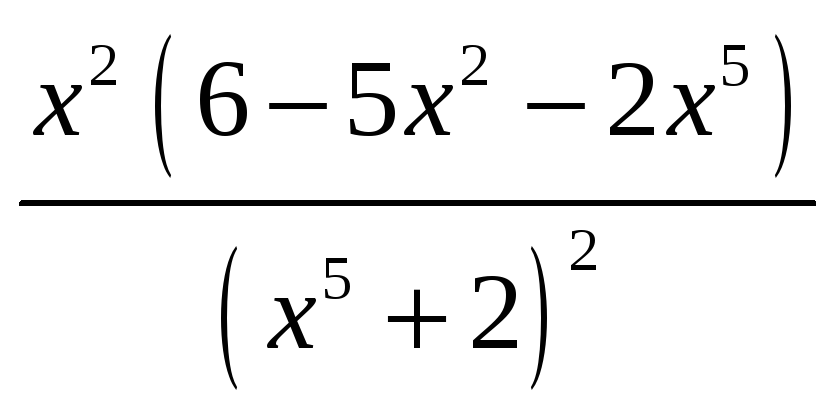в)
,
г)
30. 2.229. a)
,
б)
,
в)
,
г)
.
2.230.
2.231.
.
2.232.
.
2.233.
а)
,
б)
2.234.
а)
,
б)
.
2.235.
а)
,
б)
.
2.236.
а)
,
б)
.
2.237.
а)
,
б)
,
в)
,
г)
2.238.
а)
,
б)
.
2.
239. а)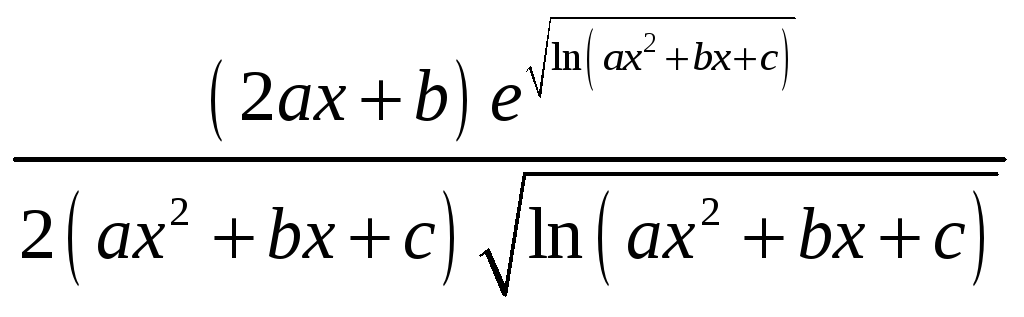
,
б)
.
2.240.
а)
,
б)
.
2.241.
а)
,
б)
.
2.242.
а)
,
б)
.
2.243.
а)
,
б)
.
2.244.
а)
,
б)
.
2.245.
а)
,
б)
.
2.246.
а)
,
б)
.
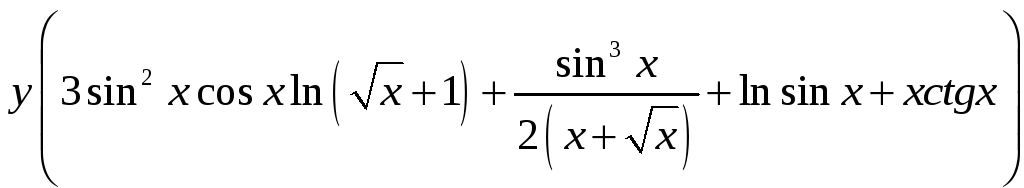2.247.
а)
,
б)
.
2.248.
а)
,
б)
.
2.249.
а)
,
б)
.
2.250.
а)
,
б)
.
2.251.
а)
,
б)
.
2.252.
.
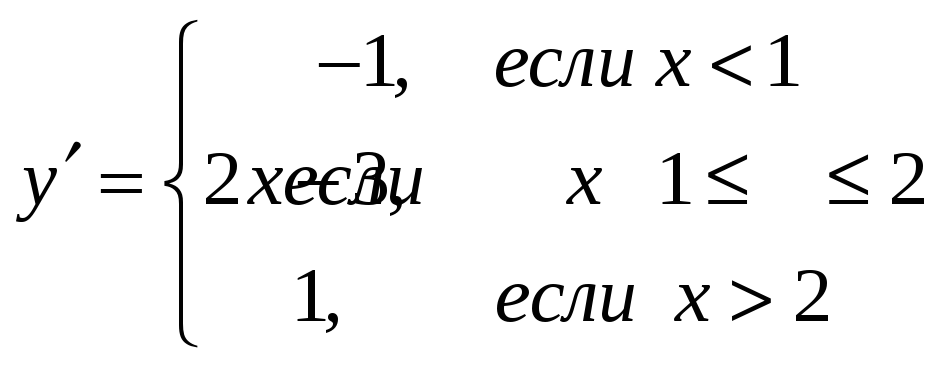2.253.
.
2.254.
а)
,
б)
.
2.255.
а)
,
б)
.
2.256.
а)
,
б)
.
2.257.
.
2.258.
.
2.259.
.
2.260.
.
2.261.
.
2.
262.
.
2.263.
.
2.
264.
.
2.265.
.
2.266.
.
2.267.
.
2.268.
.
2.269.
.
2.270.
.
2.
271.
2.272.
.
2.273.
.
2.
274.
.
2.275.
.
2.276.
.
2.277.
.
2.278.
.
2.279.
.
2.280.
.
2.281.
.
2.282.
.
2.283.
.
2.284.
.
2.285.
.
2.286.
.
2.287.
.
2.288.
.
2.289.
.
2.290.
.
2.291.
2.292.
2, 2.293.
2,
2.294.
1/3,
2.295.
1/3, 2.296.
1/128, 2.297.
1, 2.298.
1/6, 2.299.
16, 2.300.
1, 2.301.
2, 2.302.
0, 2.303.
,
2.304.
,
2.305.
0, 2.306.
1/2, 2.307.
0, 2.308.
1/2, 2.309.
1/2,
2.310.
,
2.311.
1, 2.312.
1, 2.313.
e,
2.314.
1, 2.315.
1,
2.316.
,
2.317.
e1/6.
2.318.
2,
2.319.
0.25, 2.320.
3,
2.321,
1/15,
2.322.
1, 2.323.
-12, 2.324.
2/3,
2.325.
8/11,
2.326. 11/24, 2.327. -10/3, 2.328. 0.25, 2.329. -8, 2.330. 0.15, 2.331. -2.