РГР / ТАУ практика / 1 Решение ДУ брошюра
.docМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ
РОСИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНСТВО ПО ОБРАЗОВАНГИЮ
ЮЖНЫЙ ФЕДЕРАЛЬНЫЙ УНИВЕРСИТЕТ
ТЕХНОЛОГИЧЕСКИЙ ИНСТИТУТ
ЮЖНОГО ФЕДЕРАЛЬНОГО УНИВЕРСИТЕТА В
г. ТАГАНРОГЕ
Факультет автоматики и вычислительной техники
Кафедра систем автоматического управления__
© Тесленко О.А.
Практическое занятие 1
Дисциплина «Основы автоматического управления»
Тема: Решение
линейных неоднородных дифференциальных
уравнений (ДУ)
![]() -порядка
операторным
методом
-порядка
операторным
методом
Таганрог 2010
Решение
линейных неоднородных дифференциальных
уравнений (ДУ)
![]() -порядка
операторным
методом
-порядка
операторным
методом
Краткое теоретическое введение
Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся втузов. – М.: Наука,1986.
![]() (1)
(1)
Начальные
условия 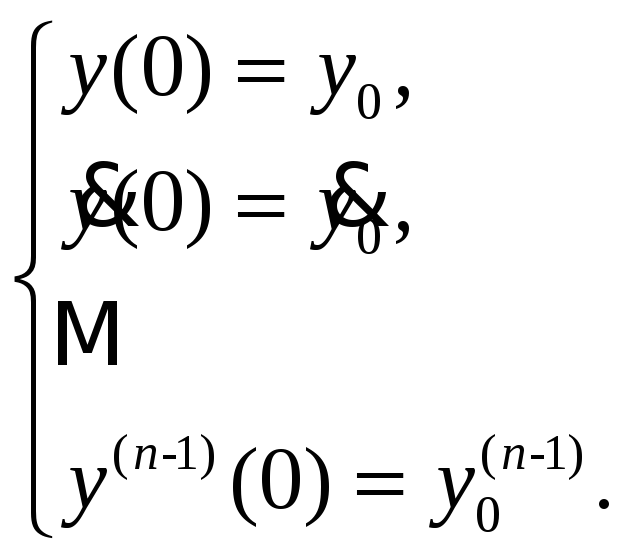 (2)
(2)
Алгоритм решения
-
Записать исходное уравнение (1) в изображениях по Лапласу с учетом начальных условий (2) (см. Табл.1)
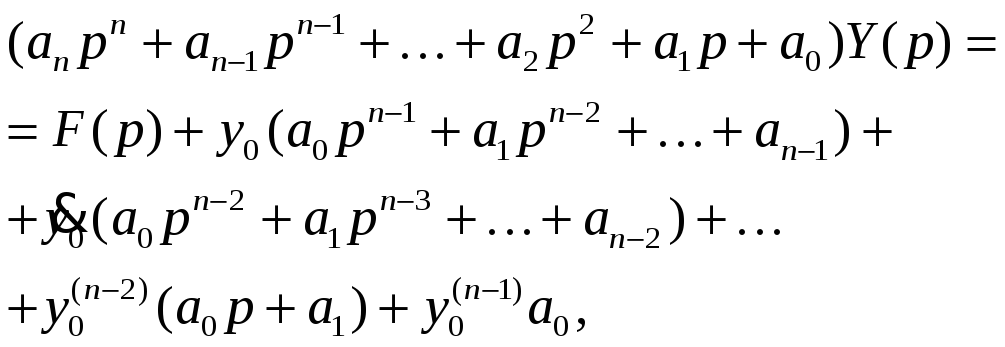 (3)
(3)
или в общем виде
![]() , (4)
, (4)
где
![]()
![]() – изображение аргумента дифференциального
уравнения,
– изображение аргумента дифференциального
уравнения,
![]() – характеристический
полином,
– характеристический
полином,
![]()
![]() – изображение
правой части ДУ (1),
– изображение
правой части ДУ (1),
![]()
![]() – изображение
начальных условий ДУ (1).
– изображение
начальных условий ДУ (1).
Таблица 1
|
оригинал |
изображение |
|
|
|
|
|
|
|
|
|
|
|
|
-
Разрешить полученное уравнение (3) относительно
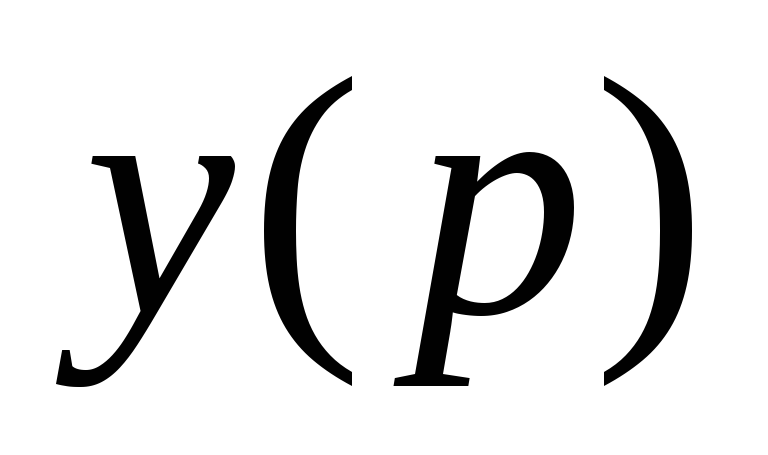
![]() .
.
-
Выполнить операцию разложения на простые дроби и определить неизвестные коэффициенты
![]() .
.
-
Если
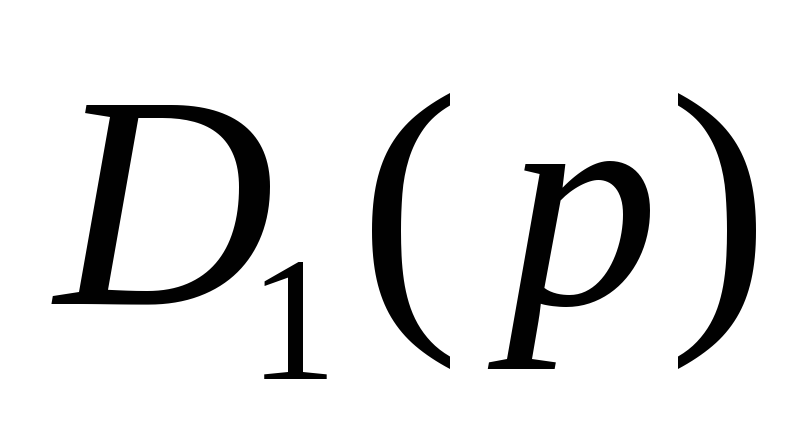 и
и
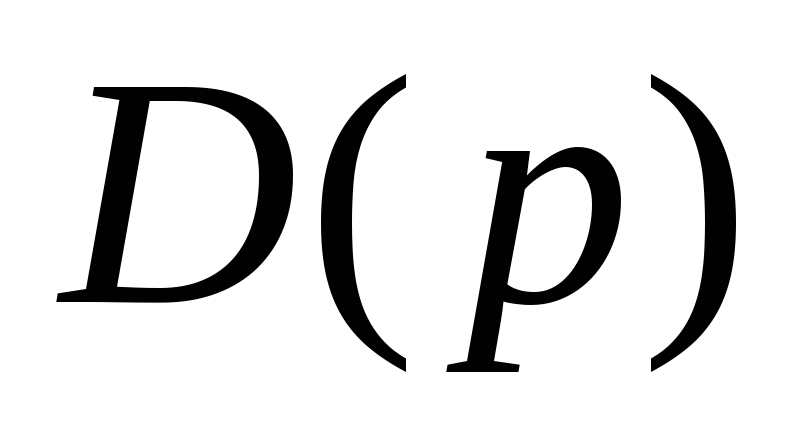 не имеют совпадающих корней, то каждому
корню
не имеют совпадающих корней, то каждому
корню
 уравнения
уравнения
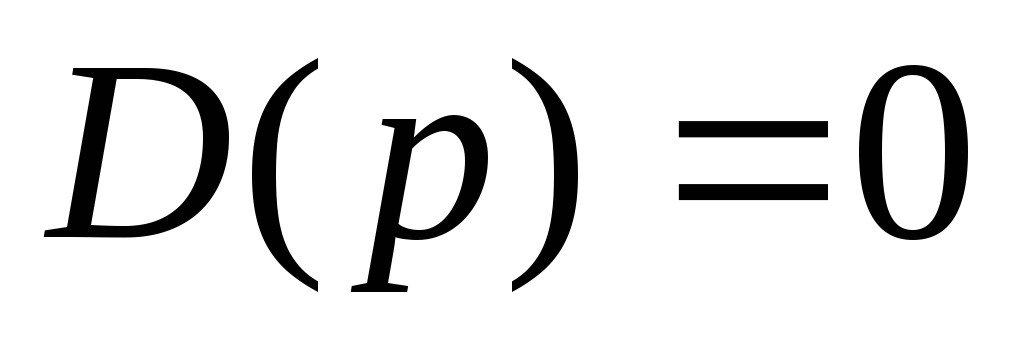 отвечает
отвечает
 -простых
дробей вида
-простых
дробей вида
![]()
![]() ,
,
где
![]() – кратность корня.
– кратность корня.
-
Каждой паре комплексно-сопряженных корней
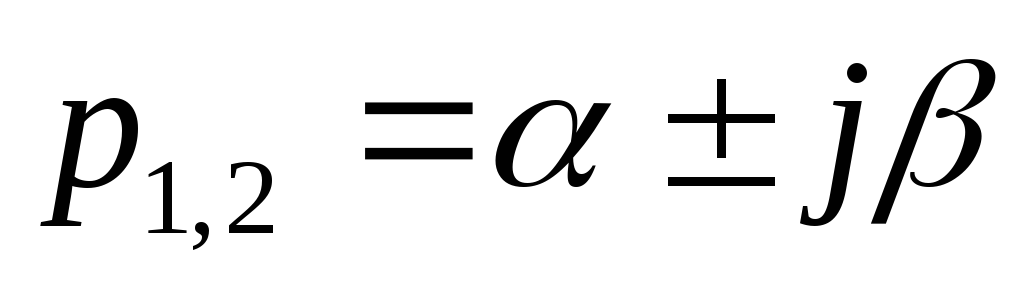 отвечает
отвечает
 -простых
дробей вида
-простых
дробей вида
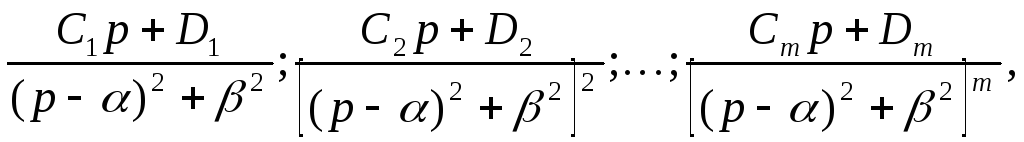
где
![]() – кратность корня.
– кратность корня.
4. Произвести обратное преобразование с помощью табл. 2 и записать решение
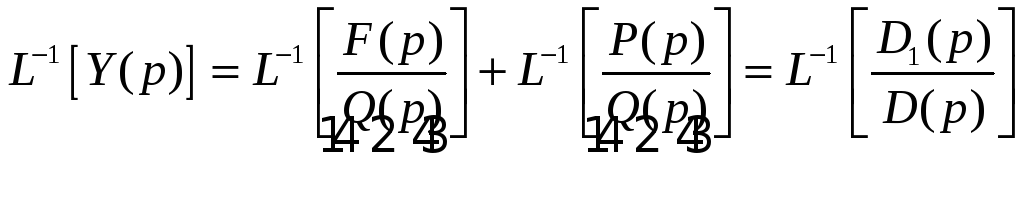

Таблица 2 преобразования Лапласа
|
Наименование |
Оригинал |
Изображение Лапласа |
|
Единичная импульсная функция |
|
1 |
|
Единичная ступенчатая функция |
|
|
|
Степенная функция |
|
|
|
Экспонента |
|
|
|
Экспонента |
|
|
|
Смещенная экспонента |
|
|
|
Синусоида |
|
|
|
Косинусоида |
|
|
|
Затухающая синусоида |
|
|
|
Затухающая косинусоида |
|
|
Пример
Дано: дифференциальное уравнение
![]() ,
,
начальные
условия
![]()
Требуется
определить:
![]()
Решение
1. ![]()
2. ![]()
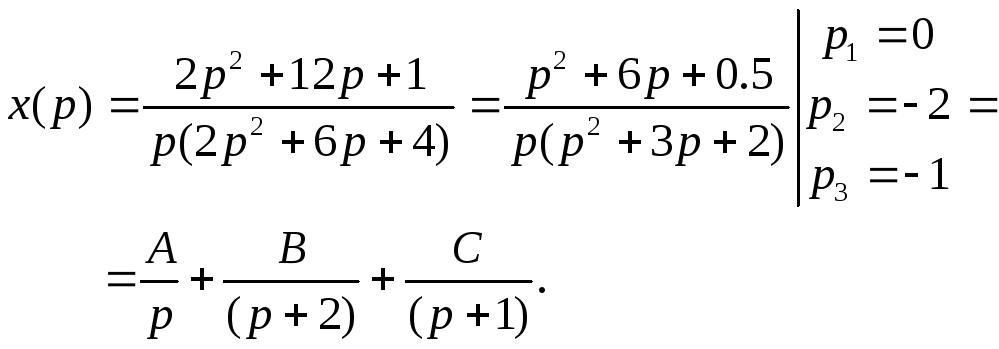
![]()
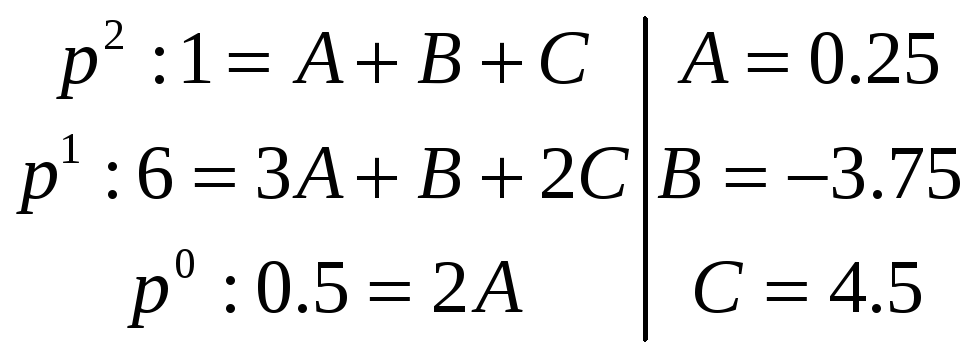
3. 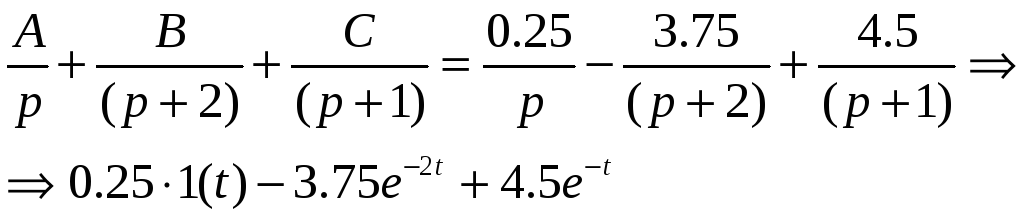
Домашнее задание
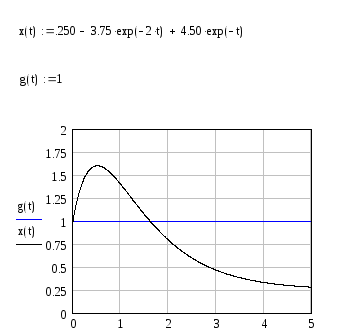
Пример решения дифференциального уравнения
в среде Mat cad
Дано: дифференциальное уравнение
![]() ,
,
начальные
условия
![]()
Требуется
определить:
![]()
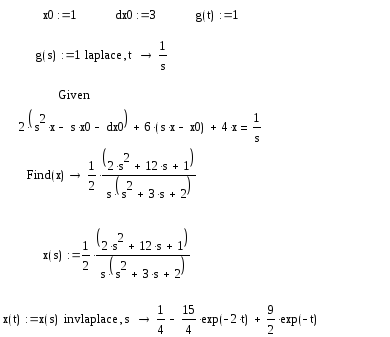
Моделирование
функции
![]() в среде Mat
cad
в среде Mat
cad