Задание д6

Считая, что при значениях S = S₁ и , взятых из задания К1 (S₁ = 0,3м, φ = 60⁰), система находится в положении равновесия, получить буквенные выражения необходимой для этого величины силы трения F_тр в промежуточной точке касания стержня АВ с направляющей опоры D. Применить принцип возможных перемещений.

Решение

Изобразим систему в заданном положении S = S₁ = 0,3 м и = 60⁰, и покажем действующие силы тяжести стержня G₁ и материальной точки G₂, а также силу трения скольжения F_тр, приложенную к стержню со стороны направляющей опоры в точке D. Реакции идеальных связей в точках О, D, А показывать не будем.

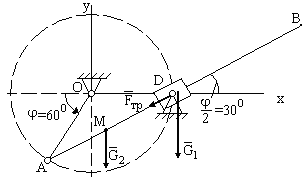
Запишем принцип возможных перемещений для системы с неидеальными связями

.

Зададим системе возможное перемещение δ и вычислим, в соответствии с принципом возможных перемещений, сумму возможных работ обозначенных на рисунке сил

.

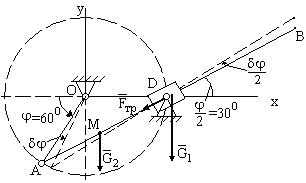
Выразим возможные перемещения δh₁, δh₂ и δS_D через δ.

Для определения δS_D следует знать, что возможные перемещения точек твердого тела относятся между собой как расстояния от этих точек до мгновенного центра скоростей Р данного тела, т.е , откуда . Отношение расстояний было найдено в задании К2, оно равно . Возможное перемещение точки А находится следующим образом: .

Величину можно найти как полный дифференциал функции , вычисленный при фиксированном времени (). Зависимость найдена в задании Д5

= – R + (АВ/2),

откуда = = .

Величину можно найти как полный дифференциал функции y_М (φ), вычисленный при фиксированном времени (). Зависимость y_М (φ) найдена в задании К1

= – R + ,

тогда = .

Подставив найденные выражения возможных перемещений в уравнение принципа возможных перемещений, получим

.

После сокращения на , найдем величину силы трения, которая сможет обеспечить равновесие системы в заданном положении

_тр = .

Задание д7

Подтвердить результаты, полученные в задании Д4, с помощью принципа Даламбера.

Решение

Принцип Даламбера говорит о том, что, «если к действующим на систему внешним силам добавить силы инерции, то получится уравновешенная система сил, для которой можно применять условия равновесия статики».

Запишем принцип Даламбера в проекциях на оси координат х и у

,

.

При решении задания на рисунке нужно показать внешние силы механической системы (они встречались в задании Д4) и силы инерции, действующие на тело АВ и точку М. Разберемся с силами инерции. Для стержня АВ, совершающего плоскопараллельное движение, силы инерции отдельных точек (или частиц) тела в общем случае приводятся к одной силе , приложенной в центре масс С₁ стержня, и паре сил с моментом . Силу инерции, действующую на точку М, обозначим .

Силы инерции направлены в сторону противоположную соответствующим ускорениям (). Момент сил инерции должен быть направлен в сторону противоположную угловому ускорению тела, но, так как угловое ускорение стержня равно нулю (смотри задание К2), значит и момент сил инерции равен нулю ( = 0) и на рисунке он не изображается.

Для того, чтобы правильно показать направления сил инерции, определим сначала величину и направление соответствующих ускорений.

Проекции на оси координат вектора ускорения центра масс стержня АВ можно найти из уравнений движения центра масс стержня, которые встречались в задании Д5

= – ОА + АС₁ = – R + (АВ/2),

= – ОА + АС₁ = – R + (АВ/2).

После вычисления производных, имеем

(),

= ().

Вычислим величины и для момента времени t = c

= () = 0,094 м/с²,

= () = 0,5038 м/с².

Так как проекции ускорения положительны (совпадают с направлением осей), то проекции силы инерции стержня АВ направлены в сторону, противоположную положительному направлению осей координат.

Найдем проекции на оси координат вектора ускорения точки М, используя для этого рисунок ускорения точки М из задания К1

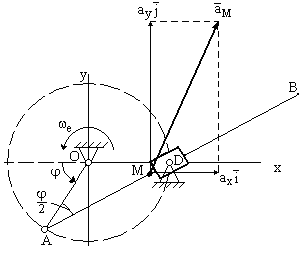
Проекции ускорения точки М на оси координат имеют вид (из задания К1)

R + R – S – S∙,

R – R –S∙ + S∙.

После подстановки  = , , , получим

R – S,

R – S.

При t = с, имеем

0,4 – 0,3 = 0,2628 м/с²,

0,4 – 0,3 = 0,6011 см/с².

Так как проекции ускорения точки М на оси координат положительны, то проекции силы инерции направлены в сторону, противоположную положительному направлению осей координат.

Изобразим все силы на рисунке.

На систему действует произвольная плоская система сил. Запишем в соответствии с принципом Даламбера условия и составим уравнения равновесия сил, причем, так как нужно определить только две неизвестных величины, то достаточно двух (из трех возможных) уравнений равновесия

,

.

В этих уравнениях обозначим = , =, где и - проекции на оси координат главного вектора внешних сил (искомые величины), которые найдем из уравнений равновесия сил

= ,

= .

Вычислим величины проекций сил инерции на оси координат

= = 15∙0,094 = 1,41 Н,

= = 15∙0,5038 = 7,557 Н.

= = 5∙0,2628 = 1,314 Н,

= = 5∙0,6011 = 3,0055 Н.

Из уравнений равновесия находим

= = 1,41 + 1,314 = 2,724 Н,

= = 7,557 + 3,0055 = 10,5625 Н.

Результаты расчетов совпадают с результатами, полученными в задании Д4.