
РГР / Nelineinie_diskretnie / 90980 ТАУ вар 8
.docВаріант 8
Раздел 2. НЕЛИНЕЙНАЯ САУ
Расчет нелинейной САУ второго порядка

Структурная схема
Задание:
-
Построение математической модели методом структурных преобразований.
-
Построение математической модели методом:
-
Фазовой плоскости
-
Изоклин
-
-
Построение переходного процесса методом:
-
Припасовывания
-
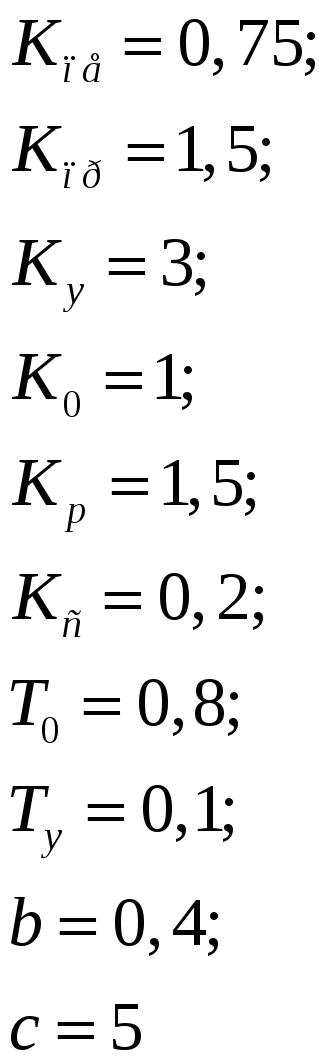
Решение
-
Побудова математичної моделі САК методом структурних перетворень
По-перше,
вузли внутрішнього контуру зворотного
зв’язку, що характеризується параметром
підсилення
![]() перенесемо. Вузол перенесемо за динамічний
елемент з параметром перетворення
перенесемо. Вузол перенесемо за динамічний
елемент з параметром перетворення
![]() ,
а суматор за елемент з коефіцієнтом
підсилення Kпе.
Отримаємо:
,
а суматор за елемент з коефіцієнтом
підсилення Kпе.
Отримаємо:

Тепер, зворотні зв’язки є паралельно з’єднаними, тому можемо зробити перетворення:

Далі, з урахуванням послідовного з’єднання можемо перетворити схему.
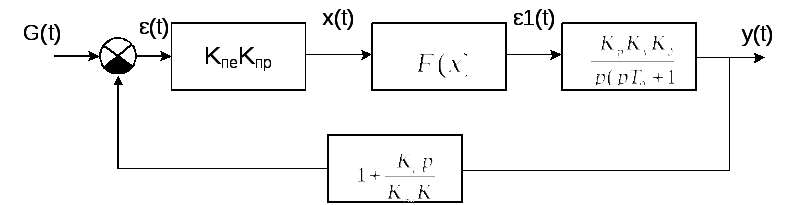
Таким чином, ми прийшли до схеми, в якій локалізовано лінійні та нелінійні елементи САК. Виходячи з цієї схеми можемо записати:
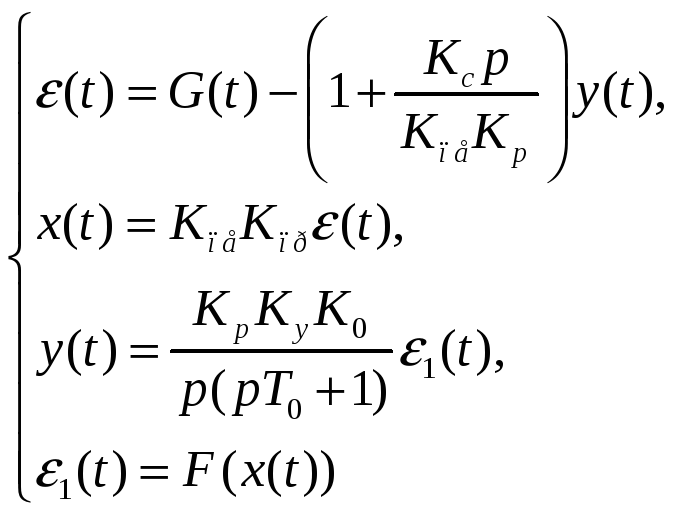
Звідки,

Звідки отримуємо рівняння, що описує нелінійну САК
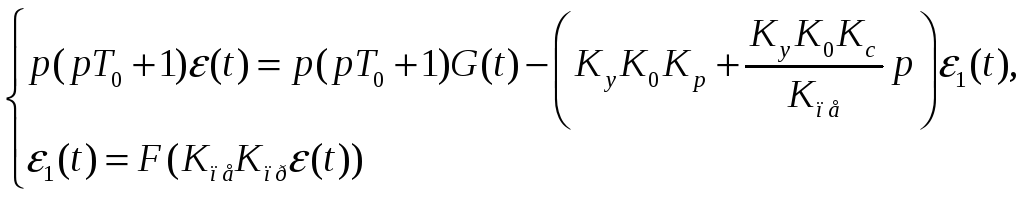
Перше рівняння описує лінійну частину, друге – нелінійну.
Тепер,
підставляємо числові дані
(![]() приймаємо
рівним 2):
приймаємо
рівним 2):
![]()
![]()
![]()
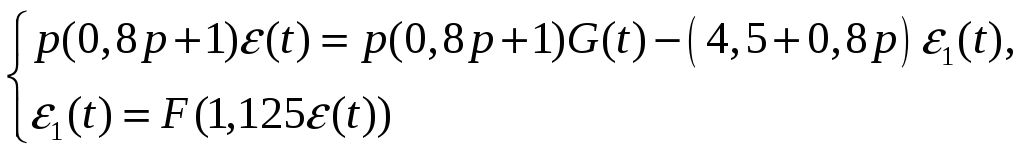
Таким чином, нелінійна САК описується нелінійним диференційним рівнянням другого порядку.
-
Метод фазової площини
Нелінійна
функція
![]() - характеристика з зоною насичення
задається рівнянням
- характеристика з зоною насичення
задається рівнянням

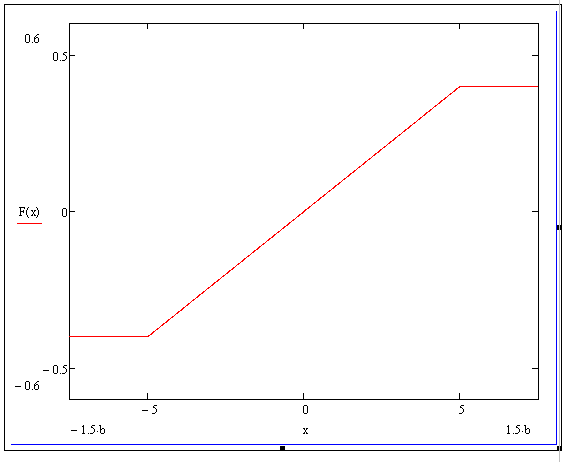
Рис. Графік нелінійної частини системи
Перепишемо систему рівнянь у вигляді

Нехай
сигнал
![]() .
Тоді,
.
Тоді,
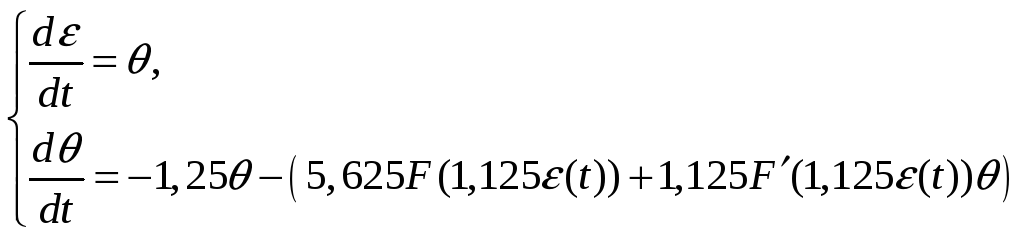
Ділимо друге рівняння на перше
![]()
Далі, розглянемо три проміжки

На першому проміжку:

Розв’язуємо це рівняння в середовищі Мathcad та будуємо фазові криві.
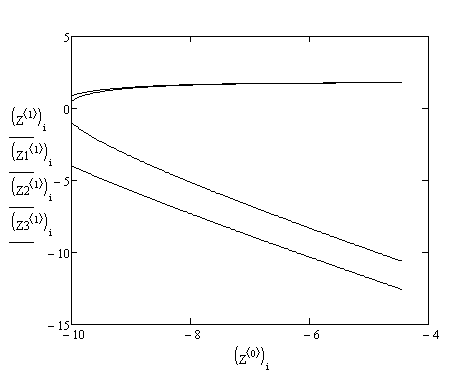
Рис. Фазові криві в першій області
Аналогічно, розв’язуємо на двох інших проміжках. Отримуємо з рівнянь графіки фазових кривих.
На другому проміжку
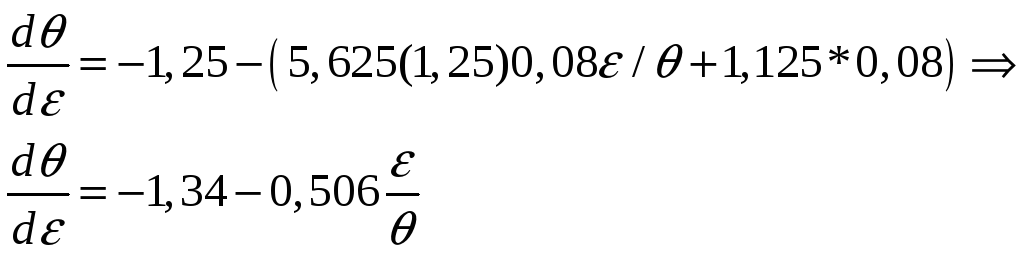
Розв’язок
рівняння можна отримати заміною
![]() .
.
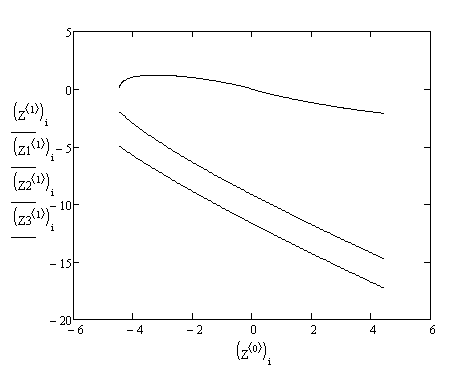
Рис. Фазові криві в другій області
На третьому проміжку

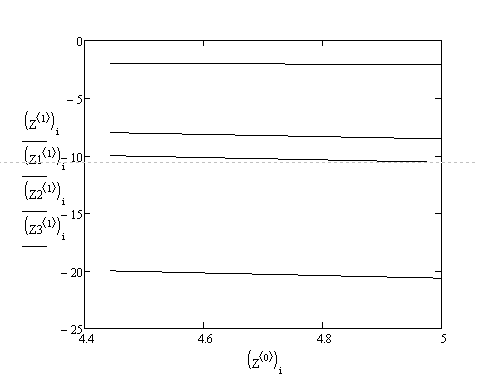
Рис. Фазові криві в третій області.
-
Метод ізоклін
В даному випадку виходимо з раніше отриманого рівняння
![]()
При цьому праву частину прирівнюємо константі.
![]()
Таким же чином як раніше розглянемо три проміжки
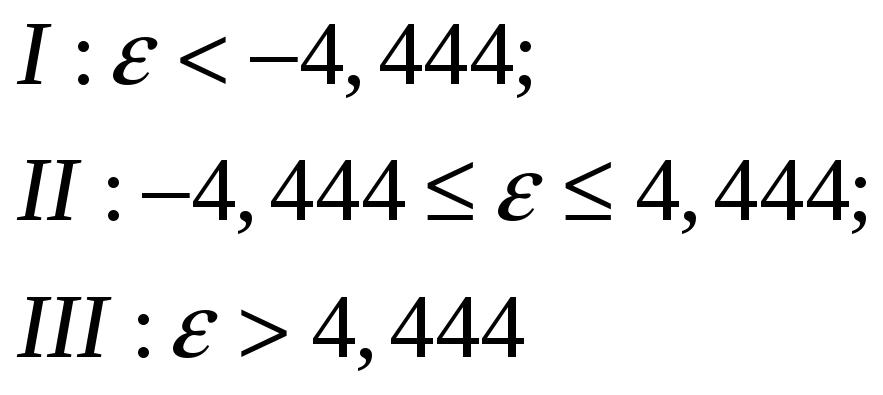
На першому проміжку
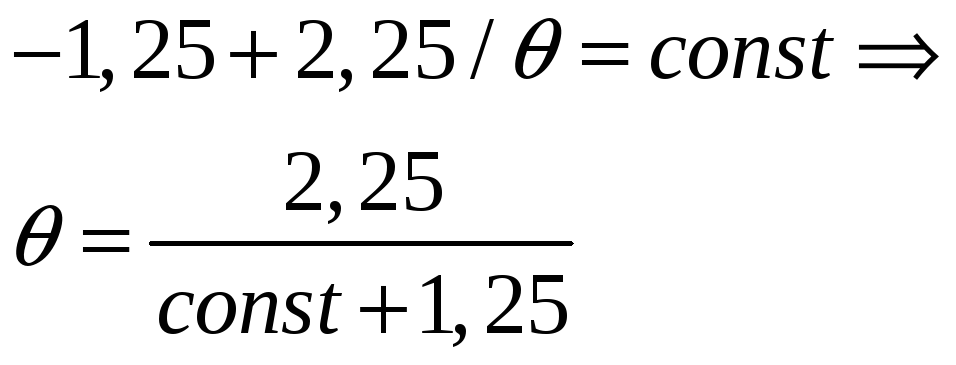
На першому проміжку ізокліни паралельні вісі абсцис.
На другому проміжку
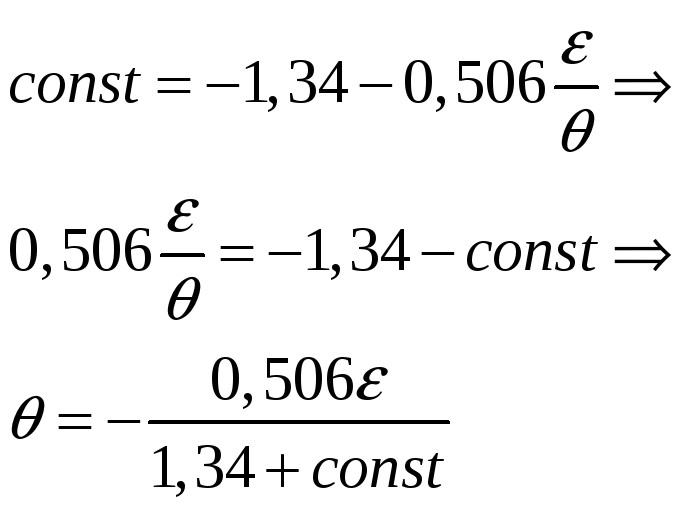
На другому проміжку вісі є прямими, що проходять через початок координат.
На третьому проміжку
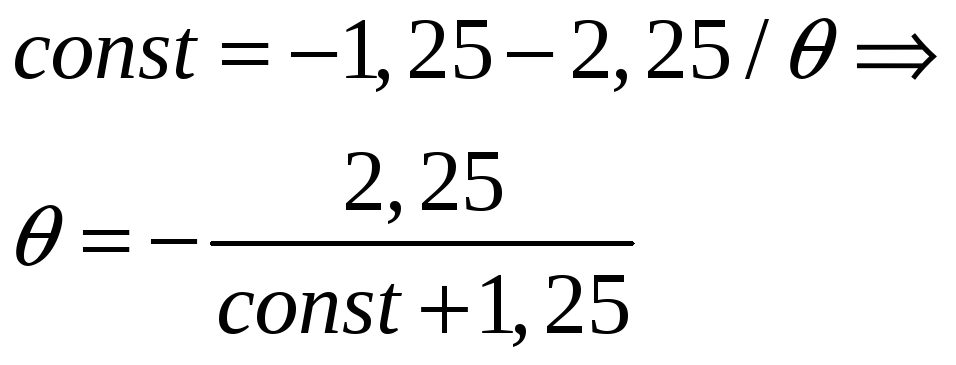
3.1. Побудова перехідного процесу методом припасовування.
Покладаємо, що вхідний сигнал одиничний З рівнянь
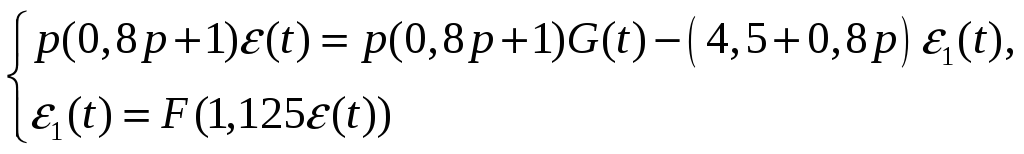
Отримуємо
![]()
Далі,
![]() .
.
Як і раніше, розглядаємо три проміжки:
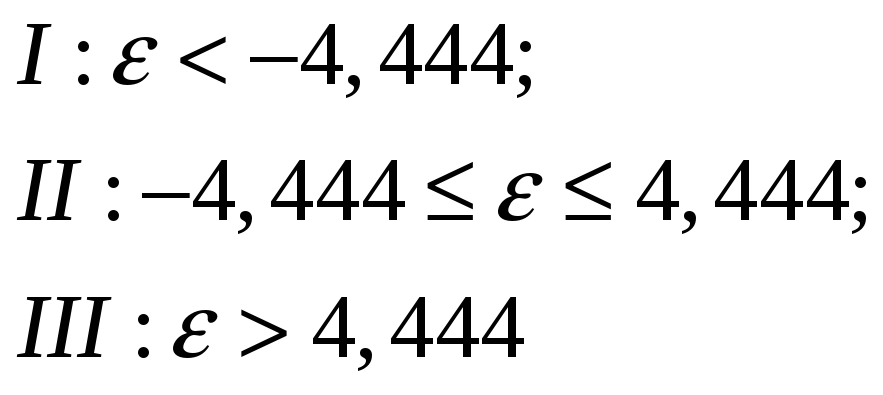
На першому проміжку
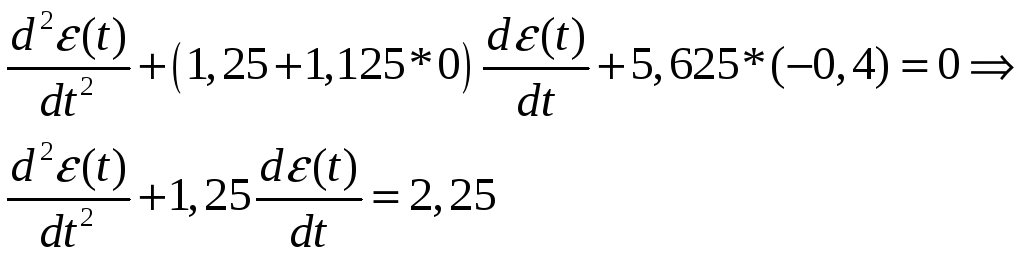
Характеристичне рівняння
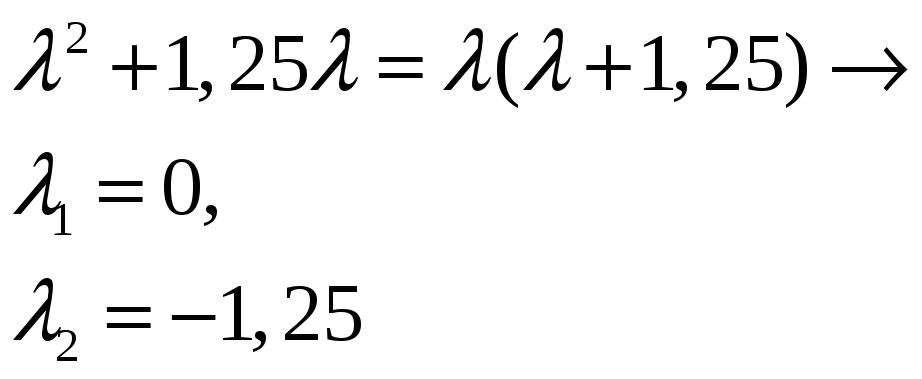
Звідки розв’язок рівняння
![]()
Задамо початкові умови
![]()
Тоді
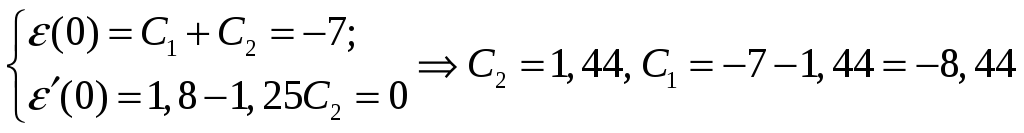
Звідки,
![]()
Визначимо, момент коли
![]()
При цьому
![]() .
.
Далі, розглядаємо рівняння на другому проміжку
![]()
Звідки,
![]()
![]()
![]()
![]()
При цьому,
![]()
З цього рівняння визначаємо константи.
Потім, визначаємо початкові умови для третього етапу розв’язку.
Розглянемо рівняння на третьому проміжку
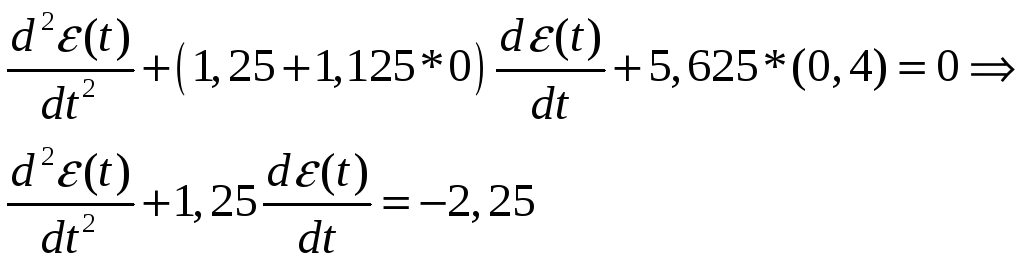
Звідки розв’язок рівняння
![]()
За значеннями отриманими на попередньому етапі отримуємо значення констант.
Таким чином, отримуємо розрахований перехідний процес в нелінійній системі.
Раздел 3. ДИСКРЕТНАЯ САУ
Расчет Дискретной САУ второго порядка
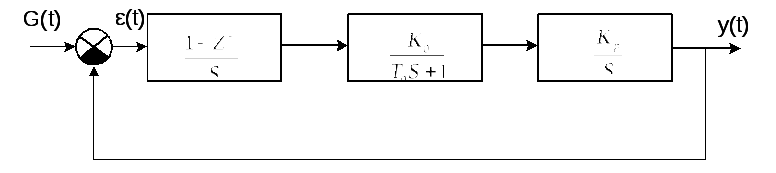
Структурная схема
Задание:
-
Составление математической модели системы
-
в
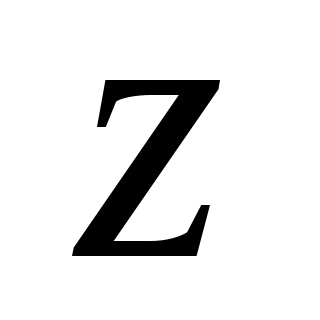 форме
форме -
В форме дискретного управления
-
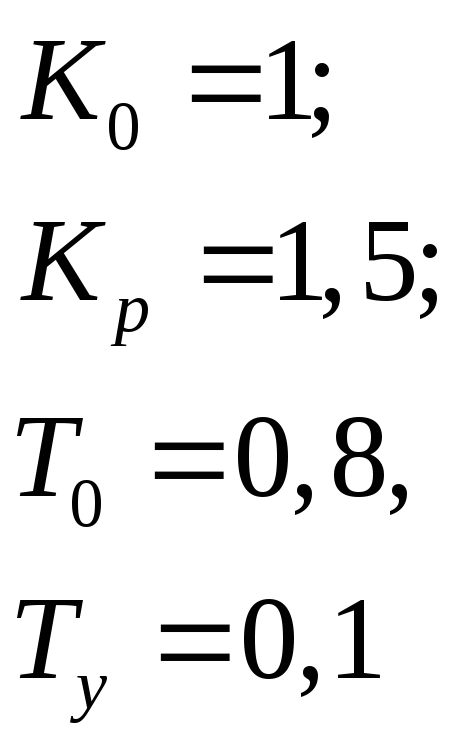
Розв’язання
1.1.
Складання математичної моделі системи
в
![]() формі
формі
Знайдемо спочатку передавальну функцію розімкненої системи. Дискретна частина являє екстраполятор нульового порядку. Передавальна функція розімкненої системи може бути записана у вигляді
![]()
Де
![]() - передавальна функція неперервної
частини.
- передавальна функція неперервної
частини.
В нашому випадку
![]() =
=![]() .
.
Тоді,
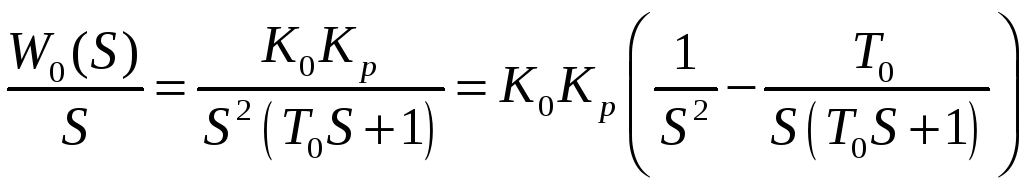
Тоді,
користуючись таблицями для
![]() -зображень
можемо знайти, що передавальна функція
розімкненої системи:
-зображень
можемо знайти, що передавальна функція
розімкненої системи:

Де
![]() ,
,
![]() -
період дискретизації.
-
період дискретизації.
Передавальна функція замкненої системи:
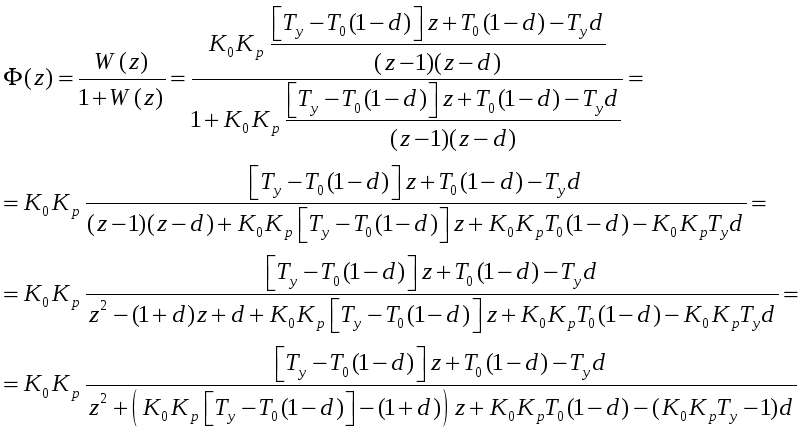
Підставляємо числові дані. Отримуємо
![]()
![]()
![]()
![]()
Звідки,
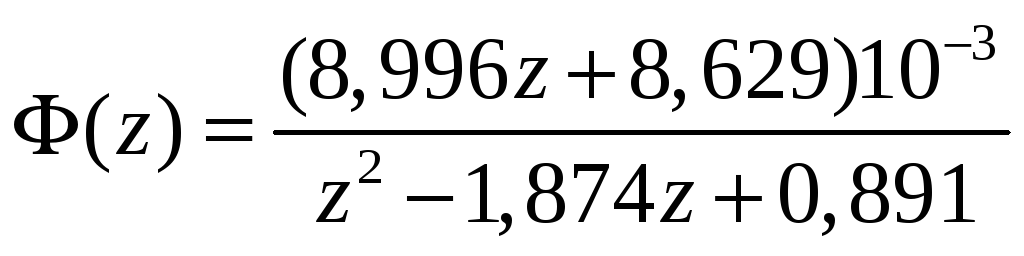
1.2. Складання математичної моделі системи в формі дискретного керування
Зображення вхідної та вихідної величин пов’язані співвідношенням
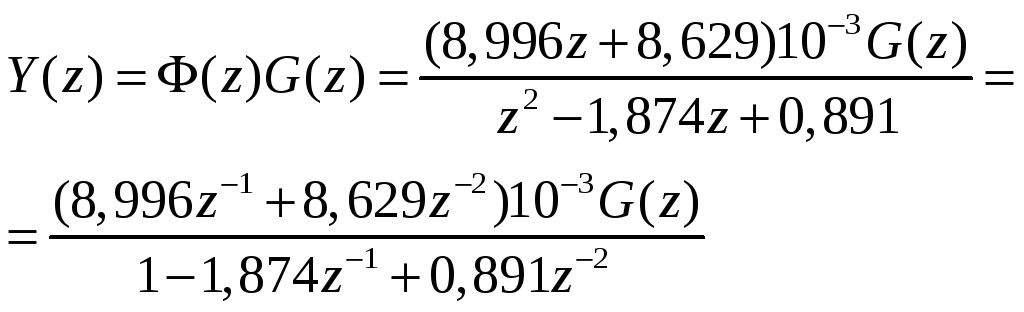
Перепишемо цю формулу у вигляді
![]() .
.
Звідки, отримуємо різницеве рівняння, що і є математичною моделлю у формі дискретного управління
![]()
