
Основные задачи динамики материальной точки.
Цель работы: знакомство с двумя основными задачами динамики материальной точки.
Задача
Д1: вычислить
и построить траекторию движения
материальной точки массой 1 кг под
действием силы ![]() ,
проекции которых на оси
,
проекции которых на оси ![]() и
и ![]() и начальные условия представлены в
табл. Д1.1 и Д1.2.
и начальные условия представлены в
табл. Д1.1 и Д1.2.
Указания: задача Д1 на интегрирование дифференциальных уравнений движения точки. Решение задачи имеет следующие этапы: составление дифференциальных уравнений, вычисление общего интеграла, нахождение закона движения материальной точки с использованием начальных условий, определение траектории точки, построение траектории точки на чертеже.
Пример
Д1: вычислить
и построить траекторию движения
материальной точки массой 1 кг под
действием силы F,
проекции которой на оси![]() и
и ![]() соответственно равны: 0 и
соответственно равны: 0 и ![]() (H),
используя начальные условия: М0
(1;4), V0=
(H),
используя начальные условия: М0
(1;4), V0=![]() .
.
|
Таблица Д1.1 (предпоследняя цифра зачетной книжки) |
|
Таблица Д1.2 (последняя цифра зачетной книжки) |
||||||
|
№ пп |
Проекция
силы на |
|
|
№ пп |
Проекция
силы на |
|
|
|
|
0 |
0 |
0 |
3 |
0 |
|
1 |
2 |
|
|
1 |
0 |
0 |
2 |
1 |
|
0 |
4 |
|
|
2 |
0 |
-2 |
1 |
2 |
|
1 |
0 |
|
|
3 |
0 |
2 |
1 |
3 |
|
1 |
0 |
|
|
4 |
0 |
1 |
2 |
4 |
2 |
2 |
3 |
|
|
5 |
0 |
-1 |
1 |
5 |
2 |
6 |
4 |
|
|
6 |
0 |
2 |
3 |
6 |
|
1 |
1 |
|
|
7 |
0 |
1 |
-2 |
7 |
|
2 |
0 |
|
|
8 |
0 |
2 |
-4 |
8 |
|
0 |
6 |
|
|
9 |
0 |
5 |
-1 |
9 |
2 |
3 |
2 |
|
Решение:
-
По второму закону Ньютона проекция силы на
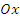 равна произведению массы материальной
точки на вторую производную от
равна произведению массы материальной
точки на вторую производную от 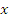 по времени
по времени 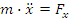 ;
т. к.
;
т. к. 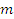 =1кг,
имеем
=1кг,
имеем 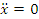 .
Интегрируя это дифференциальное
уравнение, получим
.
Интегрируя это дифференциальное
уравнение, получим 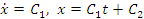 ,
где
,
где 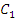 и
и 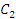 - постоянные интегрирования. Подставив
начальные условия (
- постоянные интегрирования. Подставив
начальные условия (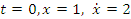 )
в данные уравнения, найдем
)
в данные уравнения, найдем 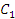 и
и 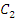 закон изменения абсциссы материальной
точки:
закон изменения абсциссы материальной
точки:
![]() .
.
-
По второму закону Ньютона проекция силы на
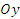 равна
равна  т.
е.
т.
е. 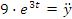 .
.
Интегрируя это дифференциальное уравнение, получим:
![]() ,
где
,
где ![]() и
и ![]() - постоянные интегрирования. Подставив
начальные условия (
- постоянные интегрирования. Подставив
начальные условия (![]() )
в данные уравнения, найдем
)
в данные уравнения, найдем ![]() и
и ![]() закон изменения ординаты материальной
точки:
закон изменения ординаты материальной
точки:
![]() .
.
-
Таком образом, уравнение движения материальной точки
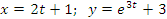 .
.
Для получения траектории следует из данных уравнений исключить параметр t:
![]() .
.
-
Построим данную кривую:
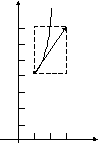 Y
Y
![]()
M0
0
X
Ответ:![]() .
.
Лабораторная работа №4.
