
Министерство образования РФ
Владимирский Государственный Гуманитарный Университет
Теоретическая механика.
Методические указания и контрольные задания.
Владимир 2010
Теоретическая механика: методические указания.
Методическая разработка предназначена для студентов; представляет собой ряд многовариантных задач по основным разделам теоретической механики, рекомендации по решению, примеры с решениями по каждому разделу.
Составитель: доцент Кошкин В. Л.
Ответственный за выпуск доцент Игонин В. А.
Печатается по решению редакционно-издательского Совета ВГГУ.
Методические указания.
В курсе теоретической механики студенты изучают три раздела: кинематику, динамику и статику.
-
Для изучения курса необходимо иметь соответствующую математическую подготовку. Во всех разделах широко используется векторная алгебра. Необходимо уметь вычислять проекции векторов на координатные оси, находить геометрически и аналитически сумму векторов, вычислять скалярное и векторное произведение двух векторов и знать свойства этих произведений, а в кинематике и динамике – дифференцировать векторы. Надо также уметь свободно пользоваться системой прямоугольных декартовых координат, знать единичные векторы (орты) этих осей и как выражаются составляющие вектора по координатным осям с помощью ортов.
Для изучения кинематики надо уметь дифференцировать функции одной переменной, строить графики этих функций, знать основы теории кривых 2-го порядка.
Для изучения динамики надо уметь находить интегралы от функций, вычислять частные производные и полный дифференциал функций нескольких переменных, а также уметь интегрировать дифференциальные уравнения 1-го порядка с разделяющимися переменными и линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами.
-
Изучать материал рекомендуется по темам или по главам учебника. Сначала следует прочитать весь материал темы, особенно не задерживаясь на том, что показалось не совсем понятным; часто это становится понятным из чтения последующего материала. Затем надо вернуться к местам, вызвавшим затруднения, и внимательно разобраться в том, что было неясно. Особое внимание при повторном чтении обратите на формулировки соответствующих определений, теорем и т. п.; в формулировках существенно каждое слово и полезно знать, почему данное положение сформулировано именно так. Не следует заучивать формулировки, важно понять их смысл и уметь изложить своими словами. Закончив изучение темы, полезно составить краткий конспект по возможности, не заглядывая в учебник.
При изучении курса особое внимание следует уделить приобретению навыков решения задач. Для этого, изучив материал данной темы надо обязательно разобраться в решениях соответствующих задач, которые приводятся в учебнике, обратив особое внимание на методические указания по их решению.
-
Закончив изучение темы, нужно проверить, можете ли вы дать ответ на все вопросы программы курса по этой теме.
Кинематика.
Лабораторная работа №1.
Траектория движения материальной точки.
Цель работы: приобретение теоретических знаний о способах задания движения материальной точки. Усвоение практических навыков вычисления параметров движения и построение траекторий движения материальной точки.
Задача
К1: материальная
точка движется в плоскости ![]() .
Закон движения задан уравнениями:
.
Закон движения задан уравнениями:
![]() ,
где
,
где ![]() и
и ![]() выражены в сантиметрах,
выражены в сантиметрах, ![]() - в секундах (табл. К1.1, К1.2). Найти:
- в секундах (табл. К1.1, К1.2). Найти:
-
Уравнение траектории движения точки;
-
Построить данную траекторию на чертеже;
-
Определить скорость, ускорение точки в момент времени
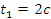 .
.
Указания:
задача К1 относится к кинематике точки
и решается с помощью формул, по которым
определяется скорость и ускорение точки
при координатном и естественном способах
задания движения. В данной задаче искомые
величины нужно определить для момента
времени ![]() .
при определении траектории движения
точки следует использовать тригонометрическую
формулу
.
при определении траектории движения
точки следует использовать тригонометрическую
формулу ![]()
Таблица К1.1 Таблица К1.2
|
(предпоследняя цифра зачетной книжки)
|
|
(последняя цифра зачетной книжки) |
||||
|
№пп |
|
|
№пп |
|
||
|
0 |
|
|
0 |
|
||
|
1 |
|
|
1 |
|
||
|
2 |
|
|
2 |
|
||
|
3 |
|
|
3 |
|
||
|
4 |
|
|
4 |
|
||
|
5 |
|
|
5 |
|
||
|
6 |
|
|
6 |
|
||
|
7 |
|
|
7 |
|
||
|
8 |
|
|
8 |
|
||
|
9 |
|
|
9 |
|
||
Пример
К1: даны
уравнения движения точки в плоскости
![]() :
:
![]()
![]() – в сантиметрах,
– в сантиметрах, ![]() – в секундах. Найти:
– в секундах. Найти:
-
Уравнение траектории точки;
-
Построить данную траекторию на чертеже;
-
Определить скорость, ускорение точки в момент времени
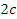 .
.
Решение:
-
Для определения уравнения траектории точки исключим из данных уравнений движения время
![]()
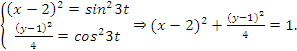
У



 равнение
траектории точки представляет собой
уравнение эллипса с центром в т. С(2;1) и
полуосями 1 и 2.
равнение
траектории точки представляет собой
уравнение эллипса с центром в т. С(2;1) и
полуосями 1 и 2.
Найдем положение
точки в момент времени
2. Скорость точки
найдем по ее проекциям на координатные
оси:
![]() .
.
![]()
![]()
![]()
![]()
![]()
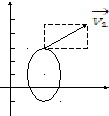 Y
Y
M1
C
O x
Рис. К1
![]() ;
; ![]()
![]()
Построим вектор
![]() на рисунке К1 в т. М1.
на рисунке К1 в т. М1.
3.Ускорение точки найдем по формулам
![]()
![]()
![]()
![]()
-8-
Ответ:![]() ;
;![]() ;
;
![]() .
.
Лабораторная работа №2.
Кинематический анализ работы плоского механизма.
Цель работы: знакомство с работой простейших плоских механизмов. Использование в практических расчетах основной теоремы кинематики, центра мгновенных скоростей. Изучение работы отдельных звеньев: кривошипа, ползуна, шатуна.
Задача
К2: плоский
механизм состоит из стержней 1-4 и ползуна
![]() ,
соединенных друг с другом и с неподвижными
опорами
,
соединенных друг с другом и с неподвижными
опорами ![]() и
и ![]() шарнирами (рис. К2.0 – К2.9). Длины стержней:
шарнирами (рис. К2.0 – К2.9). Длины стержней:
![]() .
Положение механизма определяется углами
.
Положение механизма определяется углами
![]() ,
которые вместе с другими величинами
заданы в таблице К2. Точка
,
которые вместе с другими величинами
заданы в таблице К2. Точка ![]() на всех рисунках и точка
на всех рисунках и точка ![]() на рис. 7-9 в середине соответствующего
стержня. Определить величины, указанные
в таблице в столбце «найти».
на рис. 7-9 в середине соответствующего
стержня. Определить величины, указанные
в таблице в столбце «найти».
Дуговые стрелки
на рисунках показывают углы, т. е. по
ходу или против хода часовой стрелки
(например, угол![]() на рис. 1 следует отложить от стержня
на рис. 1 следует отложить от стержня
![]() против хода часовой стрелки, а на рис.
2 – от стержня
против хода часовой стрелки, а на рис.
2 – от стержня ![]() по ходу часовой стрелки).
по ходу часовой стрелки).
Построение чертежа
начинать со стержня, направление которого
определяется углом ![]() ;
ползун
;
ползун ![]() и его направляющие для большей наглядности
изобразить, как в
и его направляющие для большей наглядности
изобразить, как в
примере К2 (см. рис.
К2). Заданную угловую скорость считать
направленной против хода часовой
стрелки, а заданную скорость ![]() – от точки
– от точки ![]() к
к ![]() .
.
Указания: задача К2 – на исследование плоскопараллельного движения твердого тела. При ее решении для определения скоростей точек механизма и угловых скоростей его звеньев следует воспользоваться теоремой о проекциях скоростей двух точек тела и понятием о мгновенном центре скоростей, применяя эту теорему (или это понятие) к каждому звену механизма в отдельности.
Предпоследняя цифра зачетной книжки
|
О 2 3
В
b
Рис. К2.0 |
A
3
O1 1 B
Рис. К2.1 |
|
О2 4
А 2 D
O1 3 B
b
Рис. К2.2 |
D B 4
Рис. К2.3 |
|
|
|
|
D B b
O1
2
O2 4 Рис. К2.4 |
3
B D
A B 1 Рис. К2.5 |
|
A
3 E 1
O1 D
B
Рис. К2.6 |
O1
2
K
4
B
O2 E Рис. К2.7 |
|
K D O2
Рис. К2.8 |
b
B
O2 Рис. К2.9 |
Таблица К2
Последняя цифра зачетной книжки
|
Номер условия |
Углы |
Дано |
Найти |
||||||||
|
|
|
|
|
|
|
|
|
||||
|
0 |
30 |
150 |
120 |
0 |
60 |
6 |
- |
- |
|
|
|
|
1 |
60 |
60 |
60 |
90 |
120 |
- |
3 |
- |
|
|
|
|
2 |
0 |
120 |
120 |
0 |
60 |
- |
- |
10 |
|
|
|
|
3 |
90 |
120 |
90 |
90 |
60 |
10 |
- |
- |
|
|
|
|
4 |
0 |
150 |
30 |
0 |
60 |
- |
4 |
- |
|
|
|
|
5 |
60 |
150 |
120 |
90 |
30 |
- |
- |
8 |
|
|
|
|
6 |
30 |
120 |
30 |
0 |
60 |
8 |
- |
- |
|
|
|
|
7 |
90 |
150 |
120 |
90 |
30 |
- |
5 |
- |
|
|
|
|
8 |
0 |
60 |
30 |
0 |
120 |
- |
- |
6 |
|
|
|
|
9 |
30 |
120 |
120 |
0 |
60 |
4 |
- |
- |
|
|
|
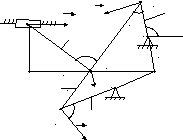 A
A
B VA 1
VB 60°
120°
-
O1
90°
C3 C2
D
2 VD O2
30°
E 4
VE
Рис. К2
Пример К2: Механизм (рис. К2) состоит из стержней 1, 2, 3, 4 и ползуна В, соединенных друг с другом с неподвижными опорами О1 и О2 шарнирами.
Дано: ![]()
![]() .
.
Определить: ![]() .
.
Решение:
-
Строим положение механизма в соответствии с заданными углами.
-
Определяем
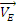 .
Точка Е принадлежит стержню АЕ. Чтобы
найти
.
Точка Е принадлежит стержню АЕ. Чтобы
найти 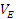 ,
надо знать скорость какой-нибудь другой
точки этого стержня и направление
,
надо знать скорость какой-нибудь другой
точки этого стержня и направление 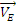 .
По данным задачи можем определить
.
По данным задачи можем определить  :
:
![]() ,
,
![]() .
.
Направление
![]() найдем,
учтя, что точка Е принадлежит одновременно
стержню О2Е,
вращающемуся вокруг О2;
следовательно,
найдем,
учтя, что точка Е принадлежит одновременно
стержню О2Е,
вращающемуся вокруг О2;
следовательно, ![]() .
Теперь, зная
.
Теперь, зная ![]() и
направление
и
направление ![]() ,
воспользуемся теоремой о проекциях
скоростей двух точек тела (стержня АЕ)
на прямую, соединяющую эти точки (прямая
АЕ). Сначала по этой теореме устанавливаем,
в какую сторону направлен вектор
,
воспользуемся теоремой о проекциях
скоростей двух точек тела (стержня АЕ)
на прямую, соединяющую эти точки (прямая
АЕ). Сначала по этой теореме устанавливаем,
в какую сторону направлен вектор
![]() (проекции
скоростей должны иметь одинаковые
знаки). Затем, вычисляя эти проекции,
находим
(проекции
скоростей должны иметь одинаковые
знаки). Затем, вычисляя эти проекции,
находим
![]() .
.
-
Определяем
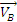 .
Точка В принадлежит стержню ВD.
Следовательно, по аналогии с предыдущим,
чтобы определить
.
Точка В принадлежит стержню ВD.
Следовательно, по аналогии с предыдущим,
чтобы определить  ,
надо сначала найти скорость точки D,
принадлежащей одновременно стержню
АЕ. Для этого, зная
,
надо сначала найти скорость точки D,
принадлежащей одновременно стержню
АЕ. Для этого, зная 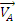 и
и 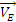 ,
построим мгновенный центр скоростей
стержня АЕ; это точка С2,
лежащая на пересечении
,
построим мгновенный центр скоростей
стержня АЕ; это точка С2,
лежащая на пересечении
перпендикуляров
![]() и
и ![]() ,
восстановленных из точек А и Е (к
,
восстановленных из точек А и Е (к ![]() и
и ![]() перпендикулярны
стержни 1 и 4). По направлению вектора
перпендикулярны
стержни 1 и 4). По направлению вектора
![]() определяем
направление поворота стержня АЕ вокруг
С2.
Вектор
определяем
направление поворота стержня АЕ вокруг
С2.
Вектор ![]() будет
перпендикулярен отрезку С2D,
соединяющему точки D
и С2,
и направлен
в сторону поворота. Величину VD
найдем из пропорции
будет
перпендикулярен отрезку С2D,
соединяющему точки D
и С2,
и направлен
в сторону поворота. Величину VD
найдем из пропорции ![]() .
.
Чтобы вычислить
![]() и
и ![]() ,
заметим, что
,
заметим, что ![]() АС2Е
– прямоугольный, т. к.острые углы в нем
равны 30 и 60°, и что
АС2Е
– прямоугольный, т. к.острые углы в нем
равны 30 и 60°, и что ![]() .
Тогда
.
Тогда ![]() АС2D
является односторонним и С2А=С2D.
в результате получим
АС2D
является односторонним и С2А=С2D.
в результате получим
![]() .
.
Так как точка В
принадлежит одновременно ползуну,
движущемуся вдоль направляющих
поступательно, то направление ![]() известно.
Тогда, восстанавливая из точек B и D
перпендикуляры к скоростям
известно.
Тогда, восстанавливая из точек B и D
перпендикуляры к скоростям ![]() и
и
![]() ,
построим мгновенный цент скоростей С3
стержня ВD.
По направлению вектора
,
построим мгновенный цент скоростей С3
стержня ВD.
По направлению вектора ![]() определяем
направление поворота стержня ВD
вокруг центра С3.
Вектор
определяем
направление поворота стержня ВD
вокруг центра С3.
Вектор ![]() будет направлен в сторону поворота
стержня ВD.
Из рис. К2 видно, что
будет направлен в сторону поворота
стержня ВD.
Из рис. К2 видно, что ![]() C3DB=30°,
а
C3DB=30°,
а ![]() DC3B=90°,
откуда С3В=
DC3B=90°,
откуда С3В=![]() 3
3
![]()
![]() 3D=
3D=![]() 3
3
![]() .
Составив пропорцию, найдем, что
.
Составив пропорцию, найдем, что
![]() .
.
-
Определяем
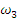 .
Так как мгновенный центр скоростей
стержня 3 известен (точка С3),
то
.
Так как мгновенный центр скоростей
стержня 3 известен (точка С3),
то
![]() .
.
Ответ:
![]() ,
,
![]() ,
,
![]() .
.
Динамика.
Лабораторная работа №3.

 1
1
 2
E
2
E
 b
2
b
2

 1 А
3
1 А
3
 O2
4
O2
4 O2
O2

 4
E 3
4
E 3