§ 1.6. Побудова початкового базисного (опорного) плану сзлп

Нехай задана СЗЛП

, (1.6.1)

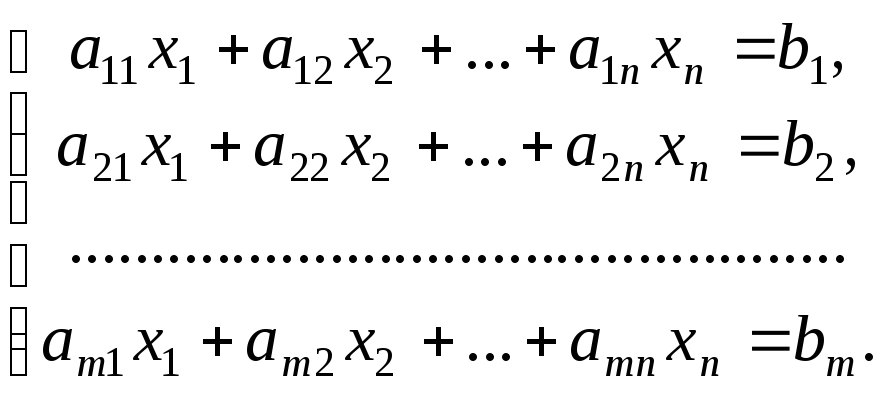(1.6.2)

, , ...,, (1.6.3)

У векторній формі задача має вигляд

,

,

.

Тут – вектор-стовпчик , .

Задачу можна записати і в матрично-векторній формі

,

,

.

Стовпцями матриці є вектори .

Якщо з якихось міркувань відомо, що змінні можуть бути базисними, то вектори-стовці утворюють базисну матрицю

.

Тоді можна отримати канонічну форму задачі у вигляді

,

,

,

де , .

Але перебір варіантів з наступним обчисленням і перевіркою умови дуже трудоємний, і з метою здійснення кроку 1 в алгоритмі симплексного методу необхідно розробити деякий регулярний метод побудови канонічної форми заданої ЗЛП.

Такий метод розроблено математиками. Він має назву – метод штучної бази. Викладемо суть цього методу.

Задачі (1.6.1) – (1.6.3) поставимо у відповідність задачу

, (1.6.4)

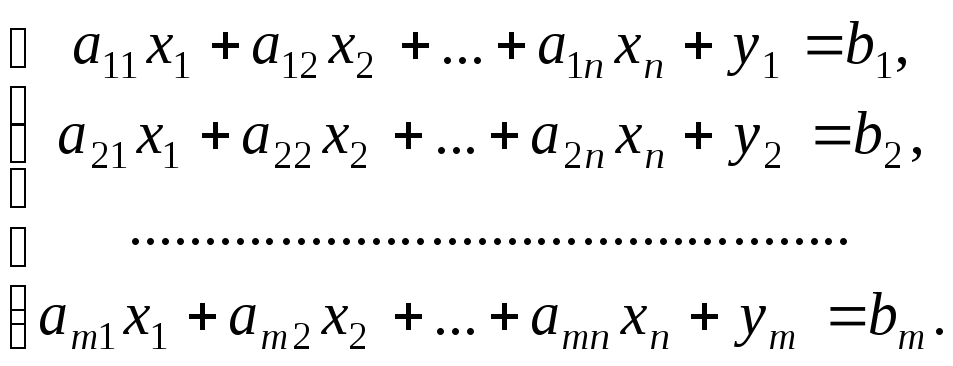(1.6.5)

, ,...,, , , …, . (1.6.6)

Ми вважаємо, що , , ..., . Якщо це не так, то відповідні рівняння системи (1.6.2) треба попередньо помножити на . Таким чином, задача (1.6.4) – (1.6.6) є ЗЛП у канонічній формі.

Для розв’язування цієї задачі можна використати симплексний метод і визначити оптимальний план

.

Вірним є таке

Твердження 1.6.1. Якщо , , ..., , то вектор є базисним (опорним) планом задачі (1.6.1) – (1.6.3). Якщо ж хоч для одного , , , то множина допустимих планів задачі (1.6.1) – (1.6.3) порожня (розв’язку не існує).

Ми не будемо доводити це твердження. З його доведенням можна ознайомитись в [1], [2].

Зробимо кілька важливих зауважень щодо використання методу.

1. Не завжди обов’язкове введення в розгляд усіх штучних змінних . Якщо, наприклад, змінна , , входить лише в одне рівняння системи обмежень (1.6.2) з коефіцієнтом одиниця, то змінної , де – номер цього рівняння, вводити в розгляд не потрібно.

2. Нехай, згідно із Твердженням 1.6.1, базисний план задачі (1.6.1) – (1.6.3). Цей вектор не обов’язково є розв’язком. Розв’язування задачі треба продовжити. Початкова таблиця симплексного методу отримується з результуючої таблиці для задачі (1.6.4) – (1.6.6) після викреслювання стовпців, відповідних штучним змінним і заміни коефіцієнтів цільової функції на коефіцієнти цільової функції . Розв’язування слід почати з перерозрахунків відносних оцінок .

Проілюструємо все на простому прикладі.

,

, .

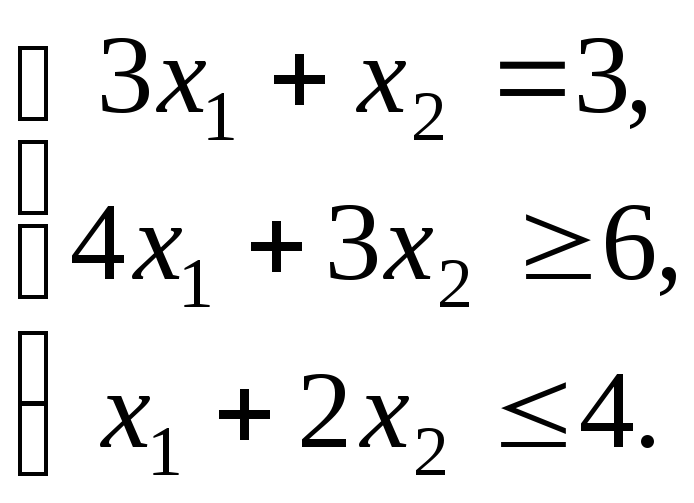
Таку задачу легко розв’язати геометрично. Ми ж використаємо симплексний метод заради ілюстрації методу штучної бази.

Перейдемо до СЗЛП, ввівши додаткові невід’ємні змінні та .

Маємо

,

, , , .

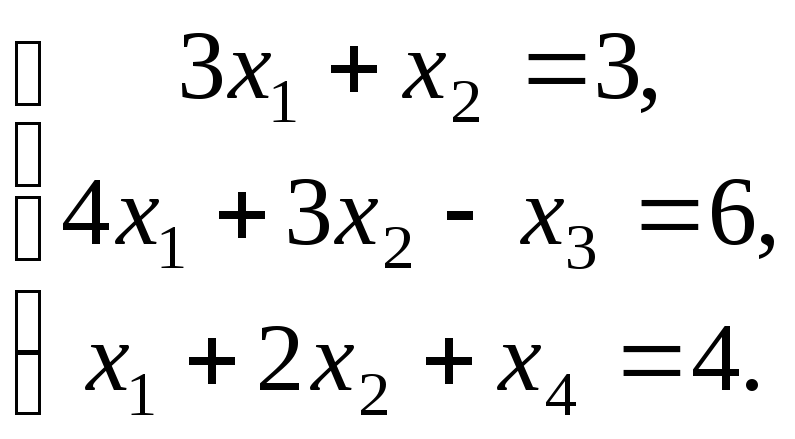
Згідно із зауваженням 1, достатньо ввести дві штучних змінних , і перейти до розв’язування допоміжної КЗЛП із початковими базисними змінними .

,

, , , , , .

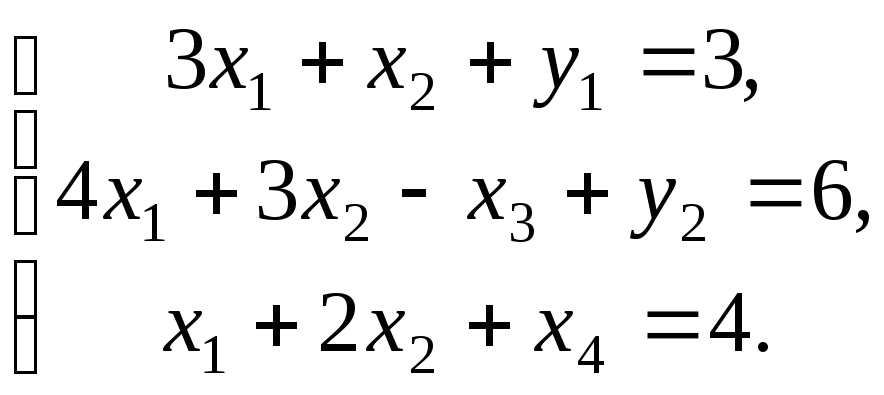
Будуємо послідовність симплексних таблиць

№ ітер.	х баз.	с баз.	0	0	0	0	1	1			Зауваження
1		1		1	0	0	1	0	3	1	ввести
		1	4	3	-1	0	0	1	6	6/4
		0	1	2	0	1	0	0	4	4	вивести
			-7	-4	1	0	0	0		9
2		0	1	1/3	0	0	1/3	0	1	3	ввести
		1	0		-1	0	-4/3	1	2	6/5	вивести
		0	0	5/3	0	1	-1/3	0	3	9/5
			0	-5/3	0	1	7/3	0		2
3		0	1	0	1/5	0	3/5	1	3/5
		0	0	1	-3/5	0	-4/5	3/5	6/5
		0	0	0	1	1	1	-1	1
			0	0	0	0	1	1		0	всі

Розв’язок допоміжної задачі має вигляд

. .

Отже, базисним (опорним) планом СЗЛП є вектор

і відповідна канонічна форма задачі має вигляд

,

, , , .

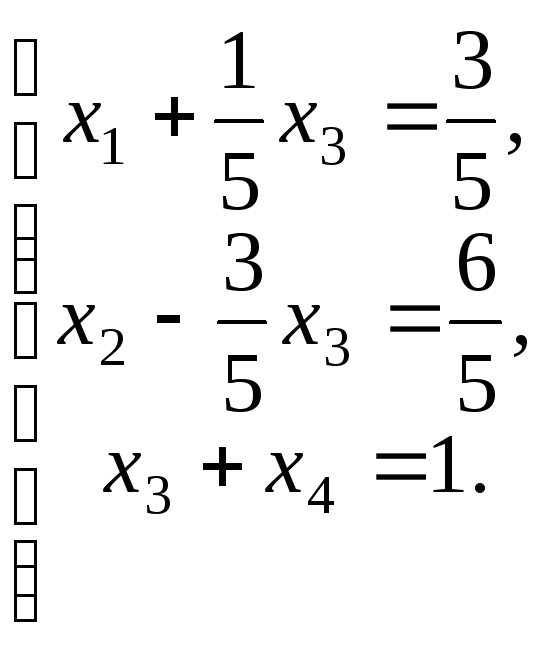
Базисними змінними є .

Будуємо симплексні таблиці

№ ітер.	х баз.	с баз.	0	0	0	0			Зауваження
1		4	4	1	0	1/5	3/5	3	ввести
		1	0	1	-3/5	0	6/5
		0	0	0		1	1	1	вивести
			0	0	-1/5	0		8/5
2		4	1	0	0	-4/5	2/5
		1	0	1	0	3/5	9/5
		0	0	0	1	1	1
			0	0	0	1/5		17/5	всі

Розв’язком стандартної задачі є вектор , а оптимальним планом заданої для розв’язування задачі – вектор . При цьому .

Іноді метод штучної бази поєднують з процесом розв’язування спеціальної задачі в канонічній формі

, (1.6.7)

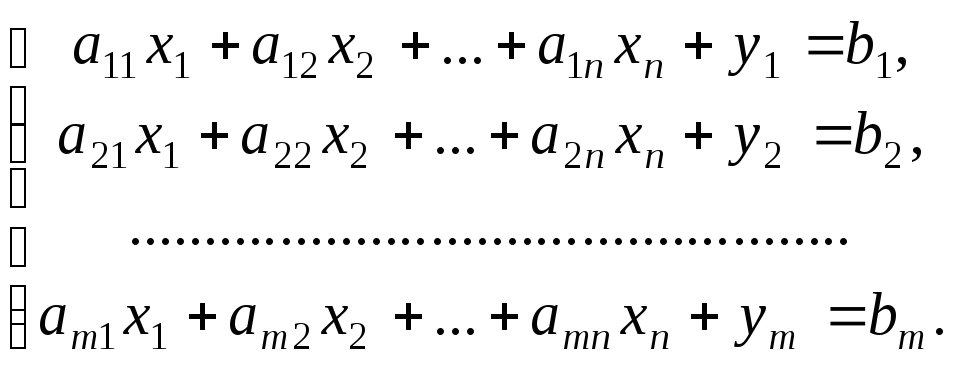(1.6.8)

, ,...,, , , …, . (1.6.9)

Тут – додатне дійсне число, більше від будь-якого числа, яке зустрічається при розв’язуванні задачі.

Після розв’язування симплексним методом задачі (1.6.7) – (1.6.9) можемо отримати один із трьох випадків:

а) в оптимальному плані задачі (1.6.7) – (1.6.9)

всі , ;

б) в оптимальному плані хоч одна із компонент більша нуля;

в) задача (1.6.7) – (1.6.9) не має розв’язку ().

Неважко довести

Твердження 1.6.2. У випадку а) оптимальним планом задачі (1.6.1) – (1.6.3) є вектор . У випадку б) множина допустимих планів задачі (1.6.1) – (1.6.3) порожня. У випадку в) цільова функція задачі (1.6.1) – (1.6.3) необмежена знизу ().

Відповідний метод розв’язування ЗЛП отримав назву -метод.

Розв’яжемо -методом СЗЛП

,

, ,...,.

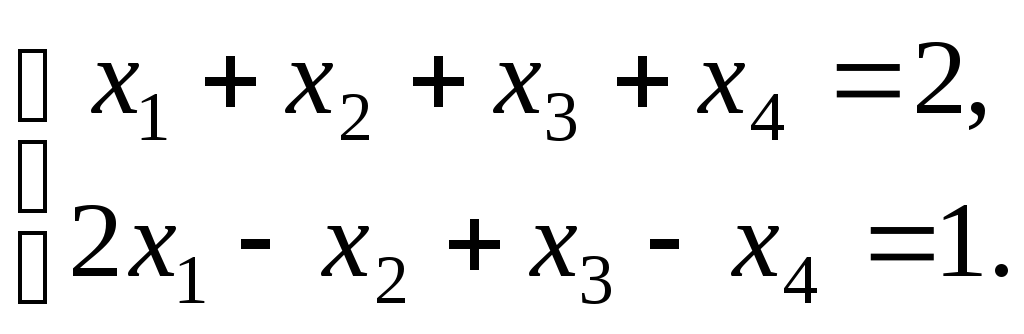
Введемо штучні змінні та і розглянемо КЗЛП

,

, ,...,,,.

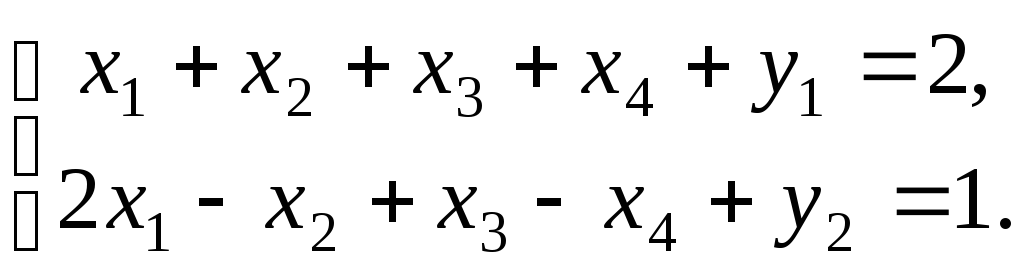
Задачу розв’язуємо симплексним методом

№ ітер.	х баз.	с баз.	-3	2	-1	-4	М	М			Заув.
1		М	1	1	1	1	1	0	2	2	ввести
		М		-1	1	-1	0	1	1		вивести
			-3М -3	2	-2М -1	-4	0	0		3М
2		М	0	3/2	1/2		1	-1/2	3/2	7/6	ввести
		-3	1	-1/2	1/2	-1/2	0	1/2	1/2		вивести
			0				0
3		-4	0	1	1/3	1	2/3	–1/3	1
		-3	1	0	2/3	0	1/3	1/3	1
			0	6	7/3	0	М+ 11/3	М– –1/3		–7	всі

Усі відносні оцінки невід’ємні. Процес розрахунків завершено.

Оптимальним планом допоміжної задачі є вектор

.

, тому, згідно із Твердженням 1.6.2, розв’язком заданої СЗЛП є

.

При цьому .

Таким чином, ми завершили ознайомлення із симплексним методом розв’язування задач лінійного програмування. На основі викладеного в розділі матеріалу можна здійснювати всі кроки наведеного у § 1.5 алгоритму.

Існують і дещо інші методи розв’язування ЗЛП. Зокрема, слід згадати так званий модифікований симплексний метод. Проте цей метод, як і методи боротьби зі згаданим в § 1.5 зациклюванням, ми розглядати не будемо. З відповідними алгоритмами можна ознайомитися, наприклад, в [2], [9], [12], [14].