Контрольные варианты к задаче 7
Вычислить пределы функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
З а д а ч а 8
Пример 10
Вычислить предел
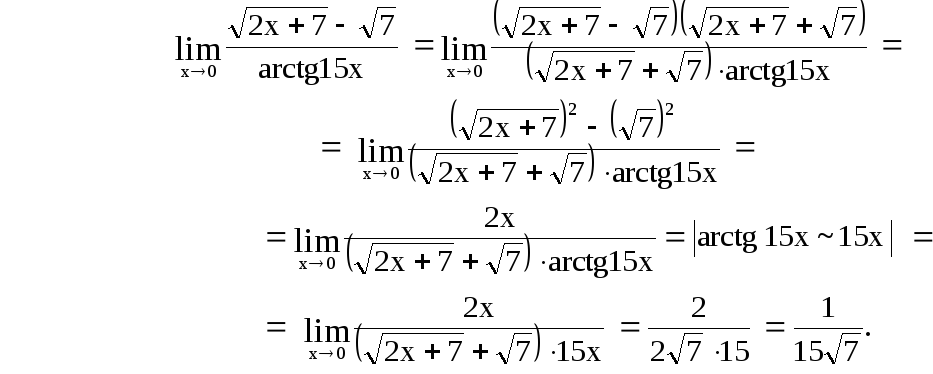
Контрольные варианты к задаче 8
Вычислить пределы функций:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
З а д а ч а 9
Пусть нужно
найти
.
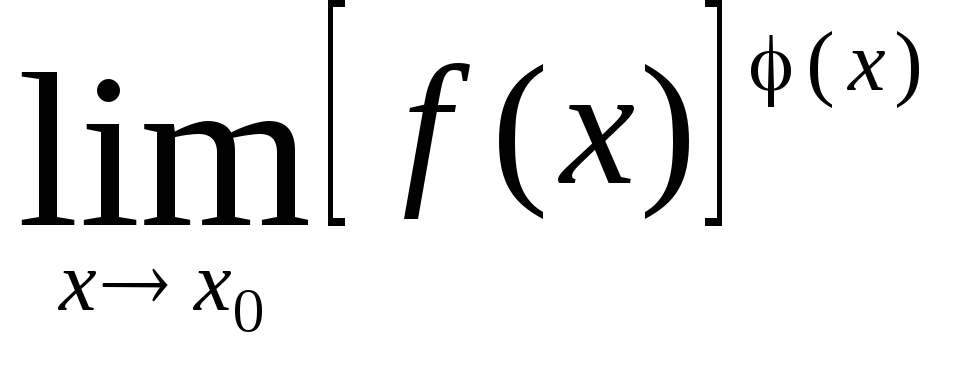Если при этом при
и
,
то имеем неопределенность
;
если
,
то имеем неопределенность
;
,
то имеем неопределенность
.
Эти неопределенности раскрываются с
помощью второго
замечательного
предела.
1.
или
2.
или
Пример 11
Вычислить
предел
.
Здесь
,
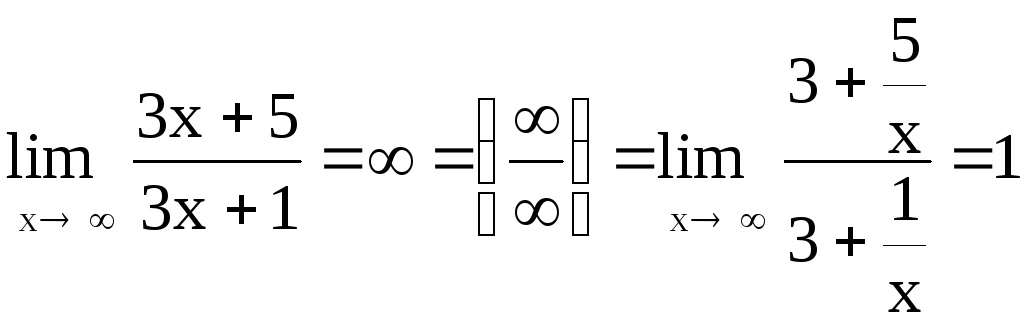поэтому
получим неопределенность
вида
.
Используем первую форму второго
замечательного предела или эквивалентность
.
Для этого преобразуем основание к виду
следующим образом:
.
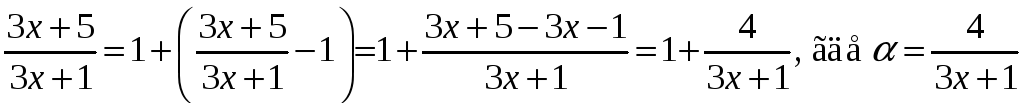Тогда
.
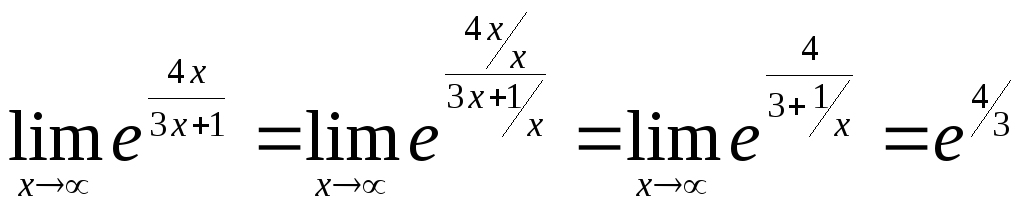Контрольные варианты к задаче 9
Вычислить пределы функций:
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
|
6. |
|
|
7. |
|
8. |
|
|
9. |
|
10. |
|
|
11. |
|
12. |
|
|
13. |
|
14. |
|
|
15. |
|
16. |
|
|
17. |
|
18. |
|
|
19. |
|
20. |
|
|
21. |
|
22. |
|
|
23. |
|
24. |
|
|
25. |
|
26. |
|
|
27. |
|
28. |
|
|
29. |
|
30. |
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
З а д а ч а 10
Пример 12
Вычислить
.
Это неопределенность вида
.
Так как
.
Найдем, используя свойство непрерывности логарифмической функции:
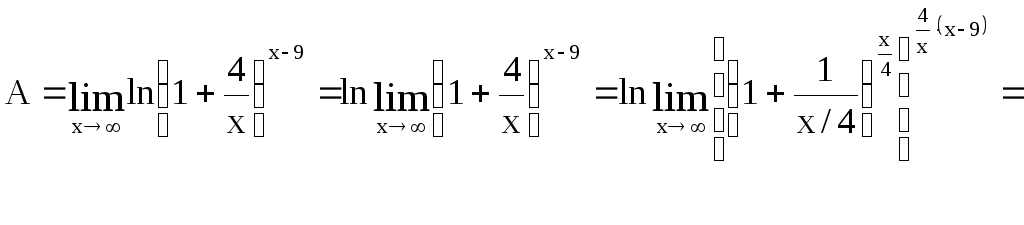
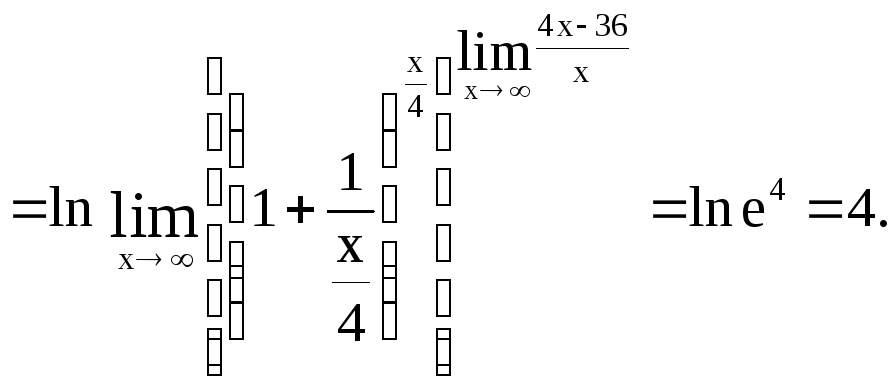
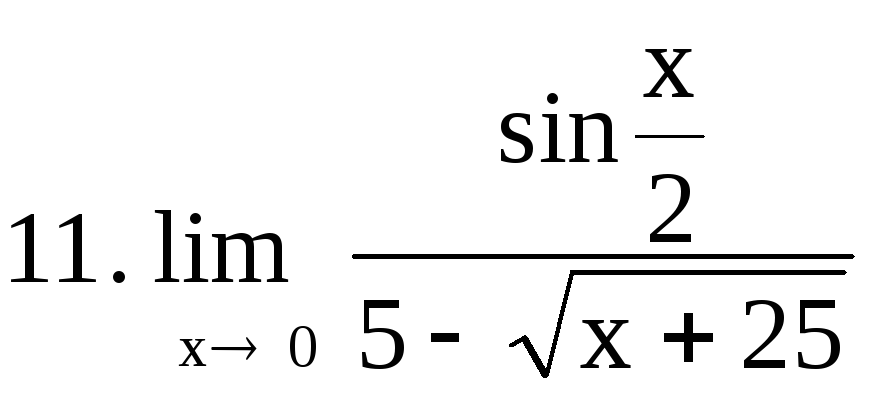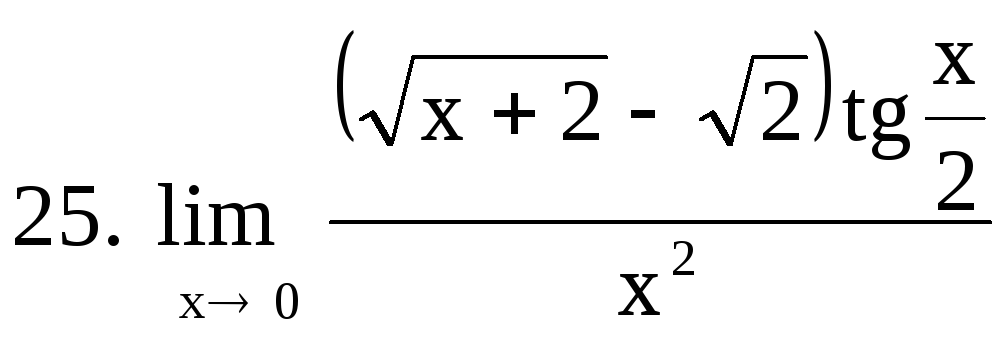