
- •Теория функций комплексного переменного
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Задачи для самостоятельного решения
- •Типовой расчет Задача 1
- •Задача 2
- •Задача 3
- •Задача 4
- •Задача 5
- •Задача 6
- •Задача 7
- •Задача 8
- •Задача 9
- •Задача 10
- •Задача 11
- •Задача 12
- •Библиографический список
- •Содержание
- •Для заметок
Задачи для самостоятельного решения
2.10.
Будет ли дифференцируемой функция
![]()
2.11.
Показать, что функция
![]() дифференцируема и найти ее производную.
дифференцируема и найти ее производную.
2.12.
При каком значении
![]() функция
функция
![]() дифференцируема?
дифференцируема?
2.13.
При каком значении
![]() функция
функция
![]() дифференцируема?
дифференцируема?
2.14.
Найти аналитическую функцию
![]() ,
если
,
если
а)
![]() б)
б)
![]() в)
в)
![]() .
.
2.15.
Найти коэффициент растяжения и угол
поворота при отображении
![]() :
:
а)
![]() в точках
в точках
![]()
б)
![]() в точках
в точках
![]() .
.
ИНТЕГРАЛ ОТ ФУНКЦИИ КОМПЛЕКСНОГО ПЕРЕМЕННОГО
Интеграл от
непрерывной функции комплексного
переменного
![]()
![]() вдоль кусочно-гладкой дуги АВ вычисляется
по формуле
вдоль кусочно-гладкой дуги АВ вычисляется
по формуле
![]() .
.
Или, если
![]() т. е.
т. е.
![]()
![]() – параметрические уравнения дуги АВ,
– параметрические уравнения дуги АВ,
![]() ~
~
![]() ,
,
![]() ~
~
![]() ,
то
,
то
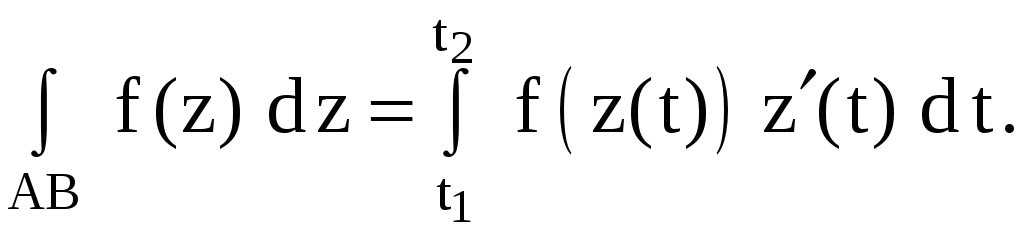
Пример 9.
Вычислить
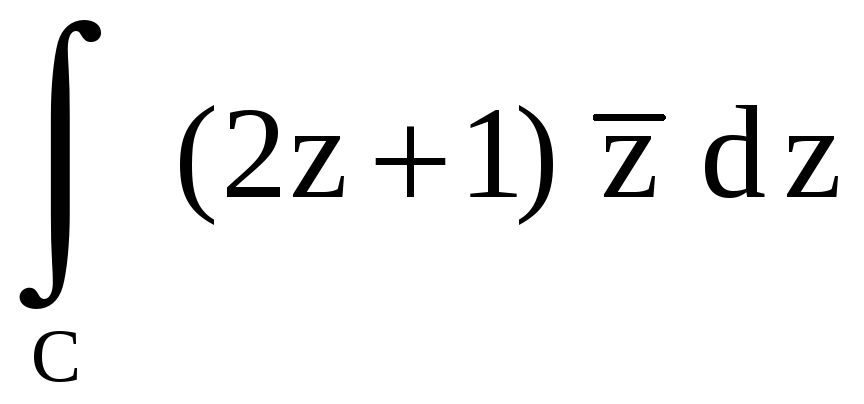 ,
если
,
если
![]() – окружность
– окружность
![]() .
.
Решение.
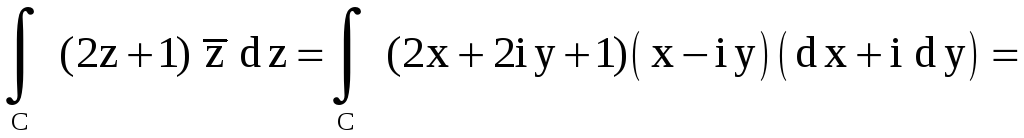
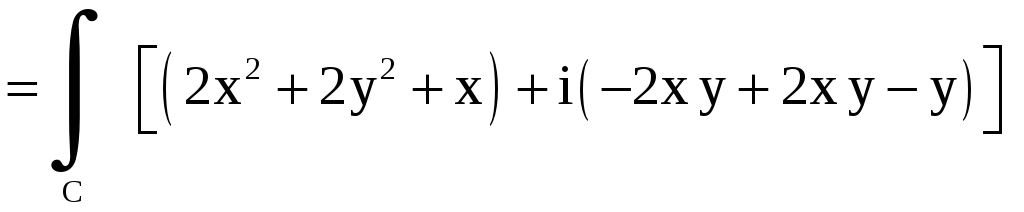
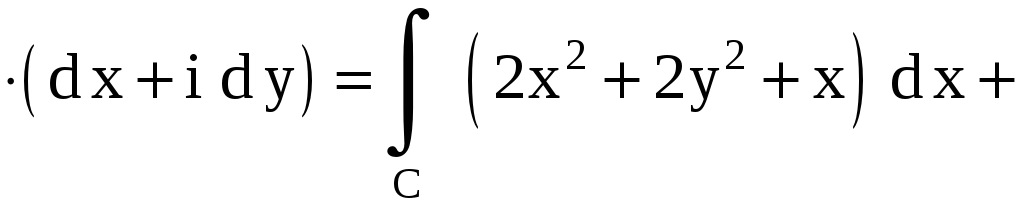
|
0 1 x
Рисунок 11 |
Для вычисления
полученных криволинейных интегралов
используем параметрические уравнения
окружности
|
Тогда
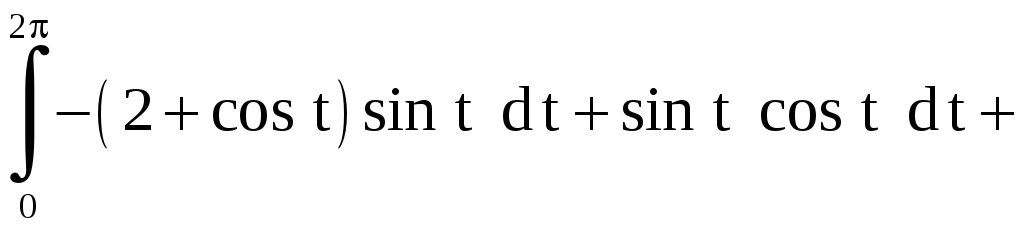
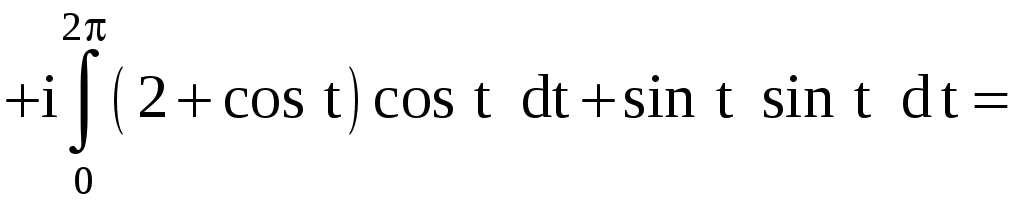
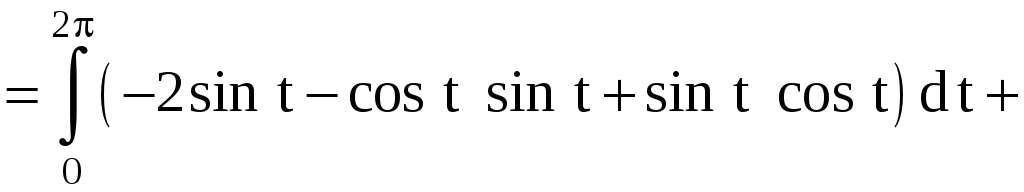
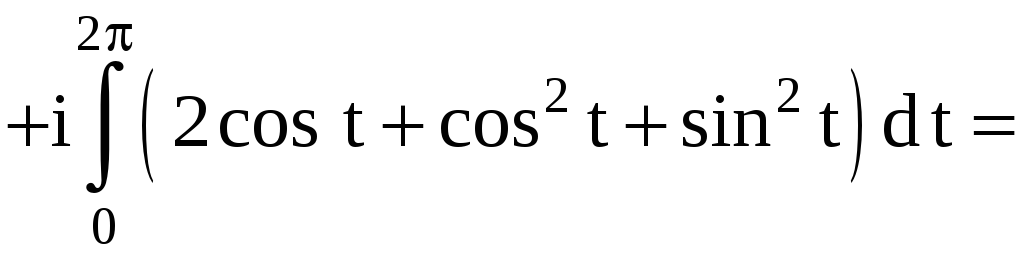
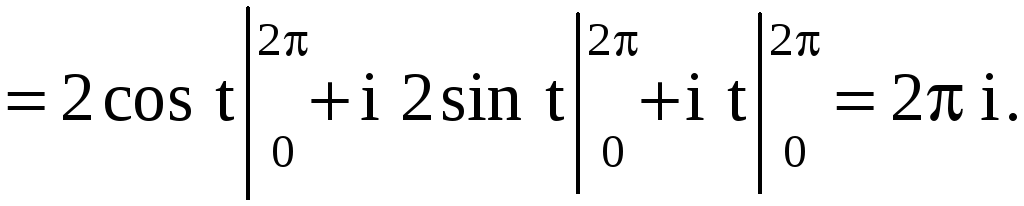
Иначе, уравнением
окружности будет
![]() .
.
Тогда
![]() .
.
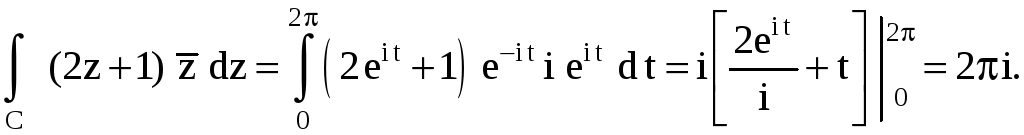
Если
![]() – аналитическая функция в односвязной
области
– аналитическая функция в односвязной
области
![]() ,
то значение интеграла
,
то значение интеграла
![]() ,
взятого вдоль произвольной кусочно-гладкой
дуги
,
взятого вдоль произвольной кусочно-гладкой
дуги
![]() ,
принадлежащей области
,
принадлежащей области
![]() ,
не зависит от дуги
,
не зависит от дуги
![]() ,
а определяется лишь положениями начальной
и конечной точек этой дуги, и вычисление
интеграла производится по формуле
Ньютона-Лейбница:
,
а определяется лишь положениями начальной
и конечной точек этой дуги, и вычисление
интеграла производится по формуле
Ньютона-Лейбница:
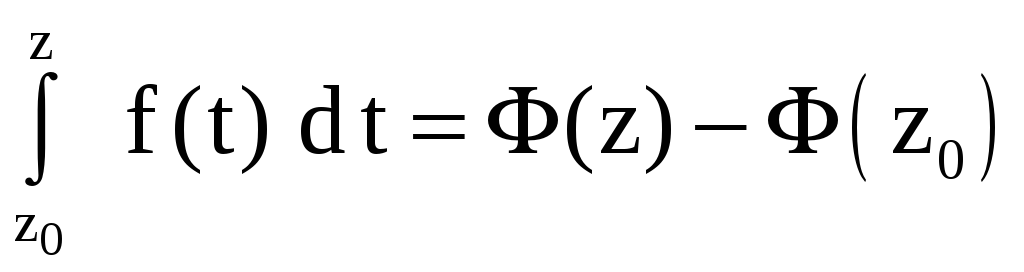 ,
,
где
![]() – какая-нибудь первообразная функция
по отношению к
– какая-нибудь первообразная функция
по отношению к
![]() .
.
Для нахождения
первообразной функции по отношению к
аналитической функции
![]() применяются обычные формулы интегрирования.
применяются обычные формулы интегрирования.
Пример 10.
Вычислить
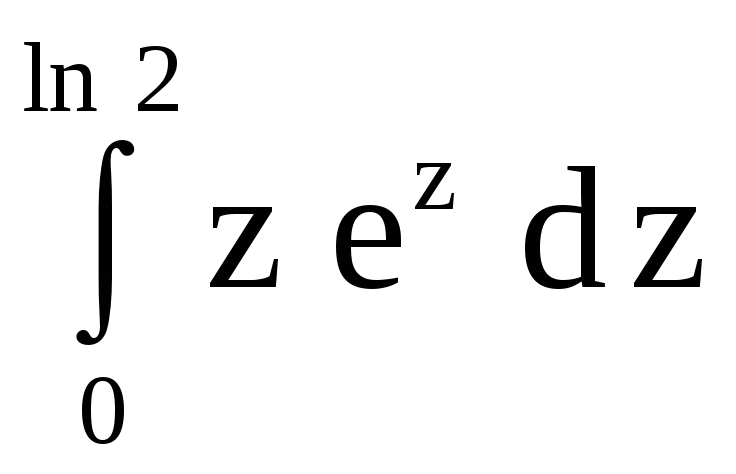 .
.
Решение.
![]() .
.
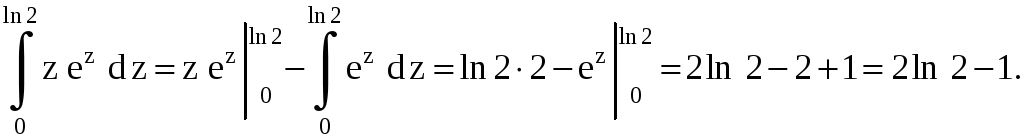
Пример 11.
Вычислить интеграл
![]() ,
где
,
где
![]() – верхняя половина окружности с центром
– верхняя половина окружности с центром
![]() единичного радиуса; направление обхода
положительное (
единичного радиуса; направление обхода
положительное (![]() – главное значение корня, получаемое
из общей формулы при
– главное значение корня, получаемое
из общей формулы при
![]() ).
).
Решение.
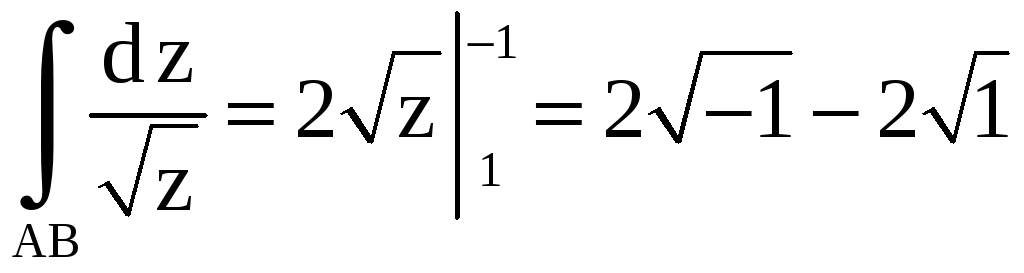 .
.
|
B 0 A x
Рисунок 12 |
При
|
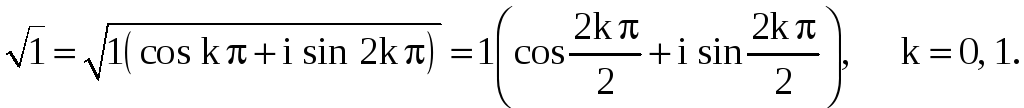
При
![]()
![]()
Основная теорема
Коши для односвязной области.
Если функция
![]() аналитична в односвязной области
аналитична в односвязной области
![]() ,
то интеграл от этой функции вдоль всякого
кусочно-гладкого замкнутого контура
,
то интеграл от этой функции вдоль всякого
кусочно-гладкого замкнутого контура
![]() ,
лежащего в
,
лежащего в
![]() ,
равен нулю.
,
равен нулю.
Пусть
![]() – простой (несамопересекающийся)
кусочно-гладкий замкнутый контур,
– простой (несамопересекающийся)
кусочно-гладкий замкнутый контур,
![]() – простые кусочно-гладкие замкнутые
контуры, лежащие внутри
– простые кусочно-гладкие замкнутые
контуры, лежащие внутри
![]() ,
но вне друг друга. Если функция
,
но вне друг друга. Если функция
![]() аналитична в многосвязной области,
лежащей между контуром
аналитична в многосвязной области,
лежащей между контуром
![]() и контурами
и контурами
![]() ,
и на этих контурах, то
,
и на этих контурах, то
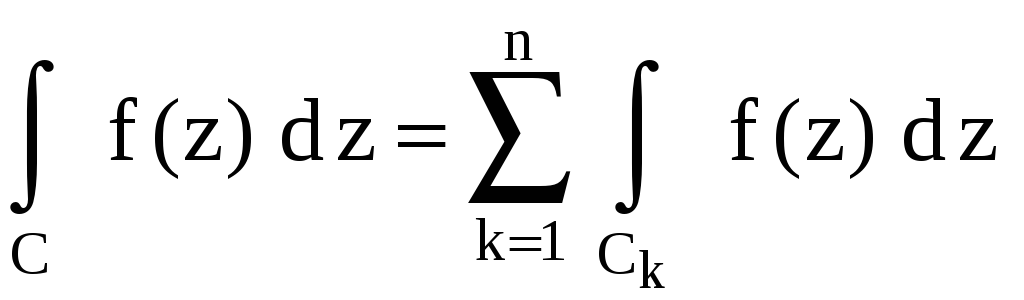 .
.
(основная теорема Коши для многосвязной области).
Пример 12.
Найти значение интеграла
![]() ,
если путь интегрирования не проходит
через начало координат.
,
если путь интегрирования не проходит
через начало координат.
Решение. Если путь интегрирования не обходит начало координат
(рис. 13а), то
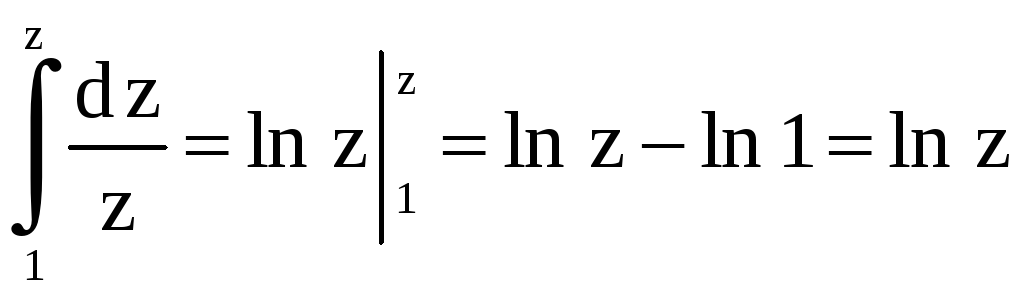 .
.
|
z
0 1 x
а) |
z С
m А 0 1 B x
б) |
z С
m А 0 1 B x
в) |
|
|
Рисунок 13 |
|
Пусть путь интегрирования обходит один раз нулевую точку в положительном направлении (рис. 13б). Тогда (рис. 13в)
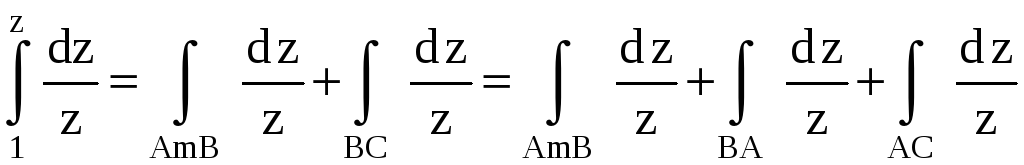 (рис. 13в);
(рис. 13в);
|
m
0 1 x
Рисунок 14 |
т.
к. в области между двумя контурами
|
Вычислим
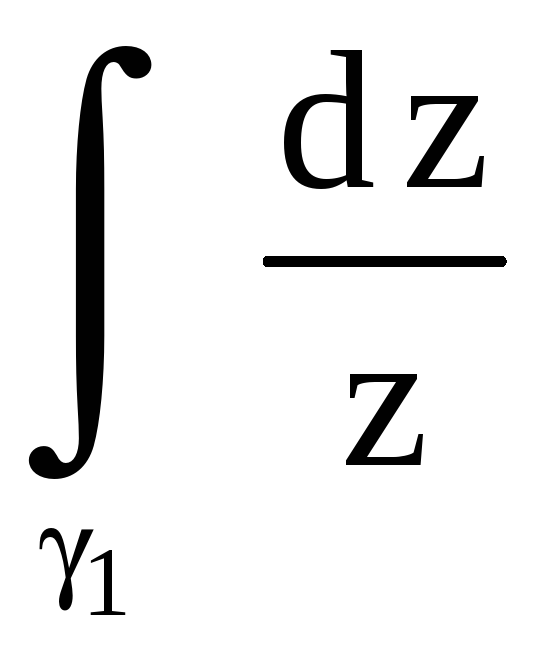 .
.
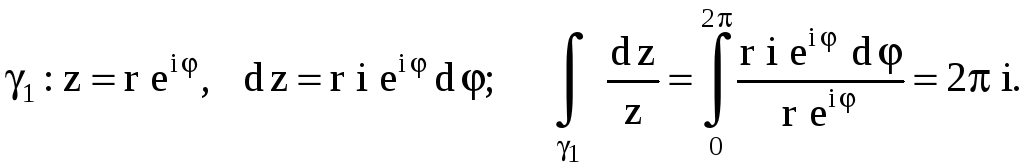
Тогда
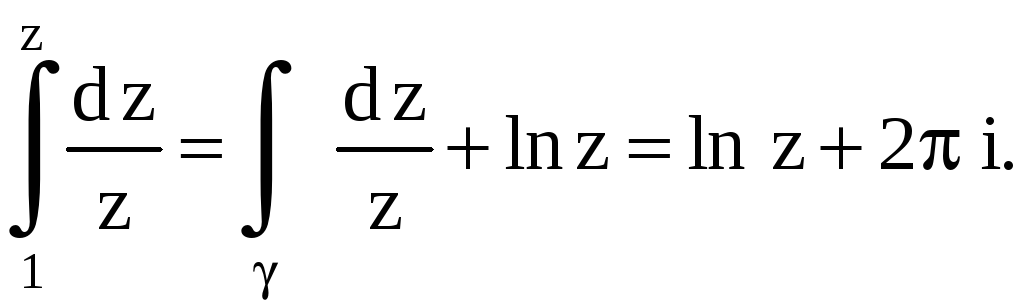
Если путь
интегрирования делает
![]() оборотов в положительном (или
отрицательном) направлении около нулевой
точки, то, очевидно, к значению
оборотов в положительном (или
отрицательном) направлении около нулевой
точки, то, очевидно, к значению
![]() прибавляется (или отнимается) число
прибавляется (или отнимается) число
![]() .
Таким образом, при всяком
.
Таким образом, при всяком
![]()
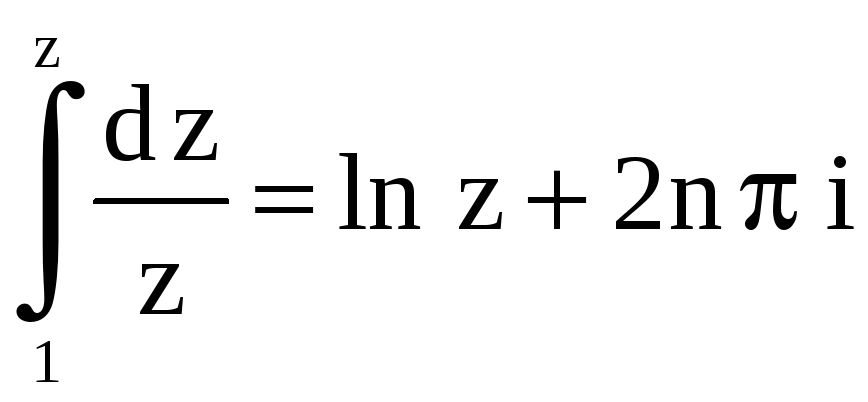 .
.
Если функция
![]() аналитична в области, лежащей внутри
простого кусочно-гладкого замкнутого
контура
аналитична в области, лежащей внутри
простого кусочно-гладкого замкнутого
контура
![]() и на этом контуре, то для любой точки
и на этом контуре, то для любой точки
![]() ,
лежащей внутри
,
лежащей внутри
![]() ,
справедливы формулы
,
справедливы формулы
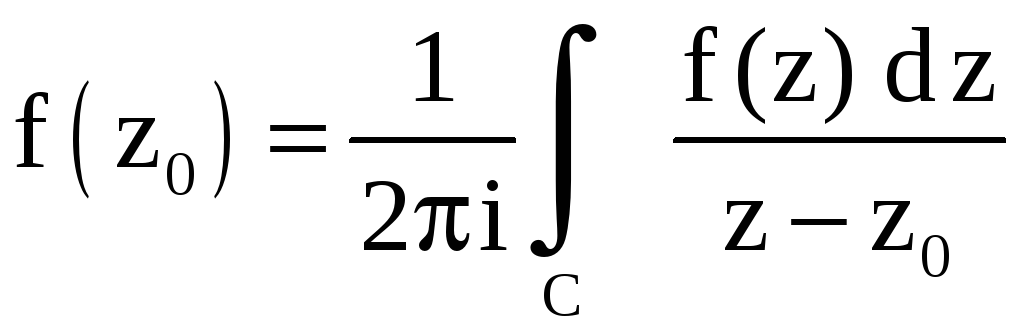 (формула
Коши),
(формула
Коши),
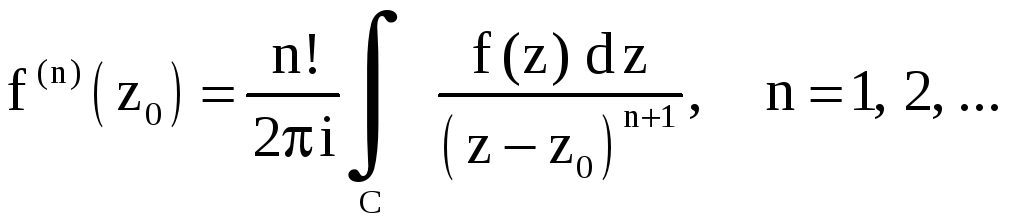 (обобщенная
формула Коши).
(обобщенная
формула Коши).
Пример 13. Вычислить
интеграл
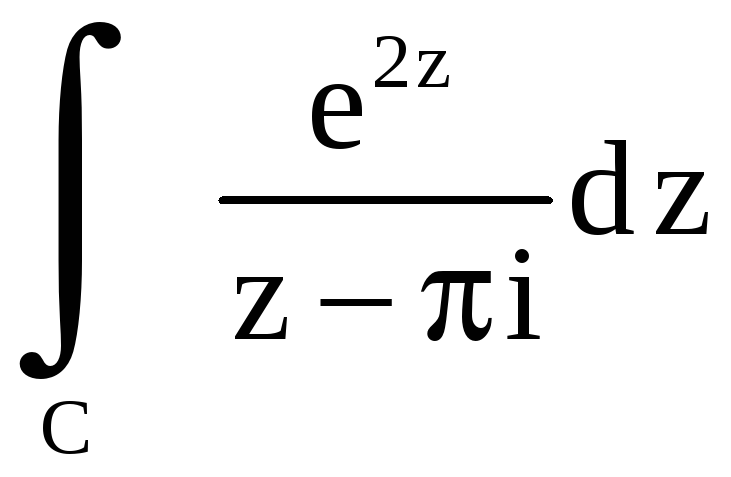 ,
,
где 1)
![]() ;
2)
;
2)
![]() .
.
Решение.
1)
![]() аналитична в круге
аналитична в круге
![]() .
Используя формулу
.
Используя формулу
|
0 4 x
Рисунок 15 |
Коши, получаем
|
2) Так как
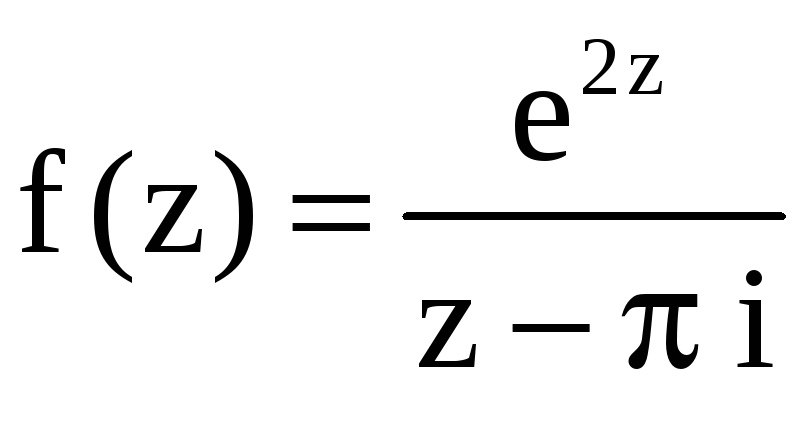 аналитична внутри области, ограниченной
окружно-
аналитична внутри области, ограниченной
окружно-
|
0 x
Рисунок 16
|
стью
|
Пример 14.
Вычислить интеграл
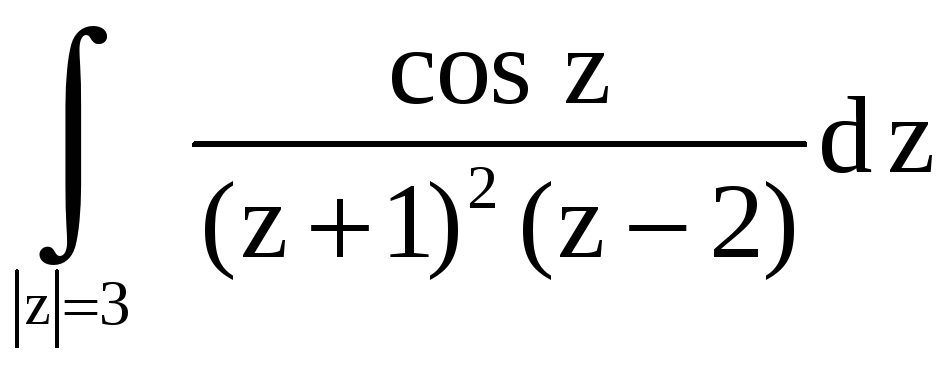 .
.
|
y
-1 2 3 x
Рисунок 17 |
Решение.
Подынтегральная
функция
Функция
|
Следовательно, по теореме Коши для многосвязной области
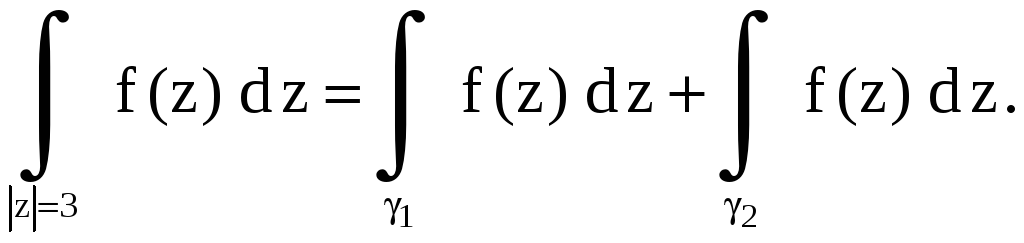
Для вычисления
интеграла по контуру
![]() применим обобщенную формулу Коши, где
применим обобщенную формулу Коши, где
![]() аналитична внутри контура
аналитична внутри контура
![]() .
.
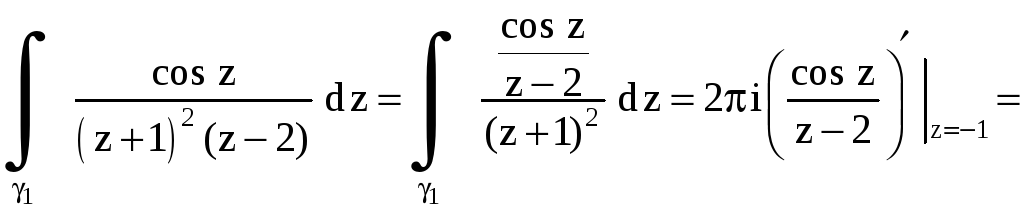
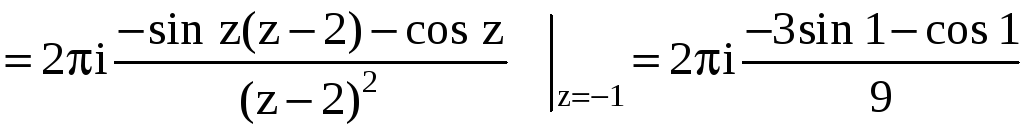 .
.
Для вычисления
интеграла по контуру
![]() применим формулу Коши, где
применим формулу Коши, где
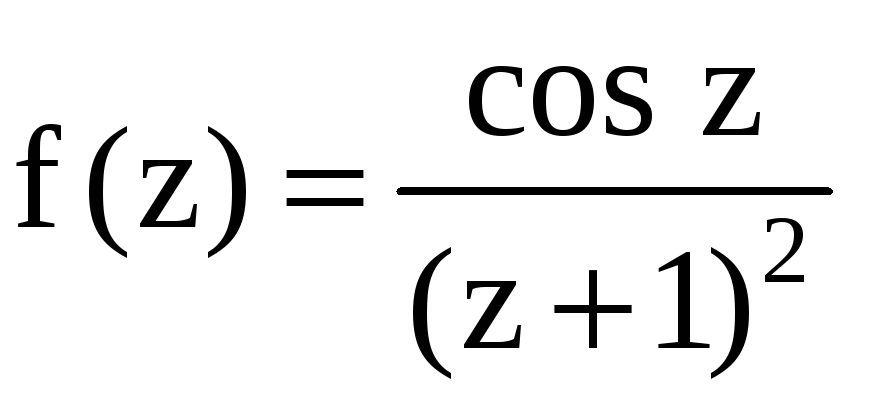 аналитична внутри контура
аналитична внутри контура
![]() :
:
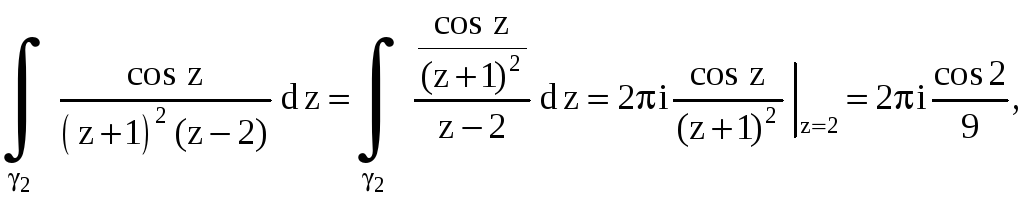
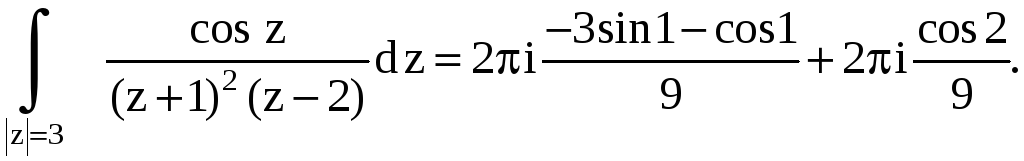
Задачи
3.1.
Вычислить
![]() ,
где
,
где
![]() – дуга параболы
– дуга параболы
![]() от точки
от точки
![]() до точки
до точки
![]() .
.
3.2.
Вычислить
![]() ,
где
,
где
![]() – прямолинейный отрезок, соединяющий
точки
– прямолинейный отрезок, соединяющий
точки
![]() и
и
![]() .
.
3.3.
Вычислить
![]() по левой полуокружности с центром в
точке
по левой полуокружности с центром в
точке
![]() и радиусом
и радиусом
![]() ,
если
,
если
![]() .
.
3.4.
Вычислить
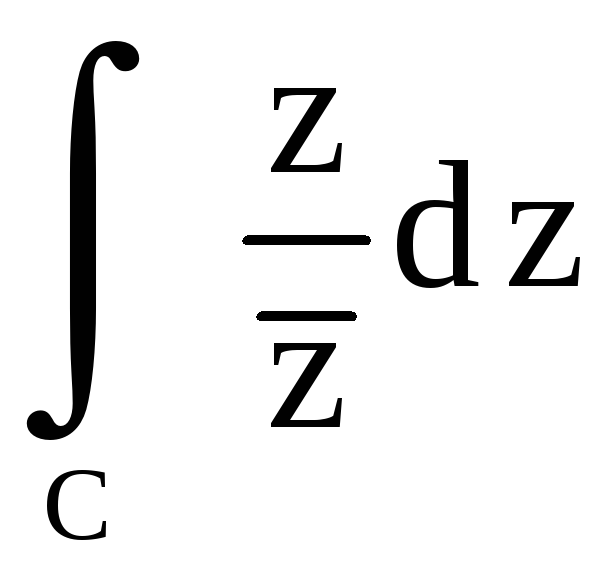 ,
где
,
где
![]() – граница области
– граница области
![]() .
.
3.5.
Вычислить
![]() ,
где
,
где
![]() – произвольная линия, соединяющая точки
– произвольная линия, соединяющая точки
![]() .
.
3.6.
Вычислить
![]() .
.
3.7.
Вычислить
![]() по следующим контурам:
по следующим контурам:
а) по полуокружности
![]() (
(![]() – ветвь,
получаемая из общей формулы при
– ветвь,
получаемая из общей формулы при
![]() );
);
б) по полуокружности
![]()
![]() .
.
3.8.
Вычислить
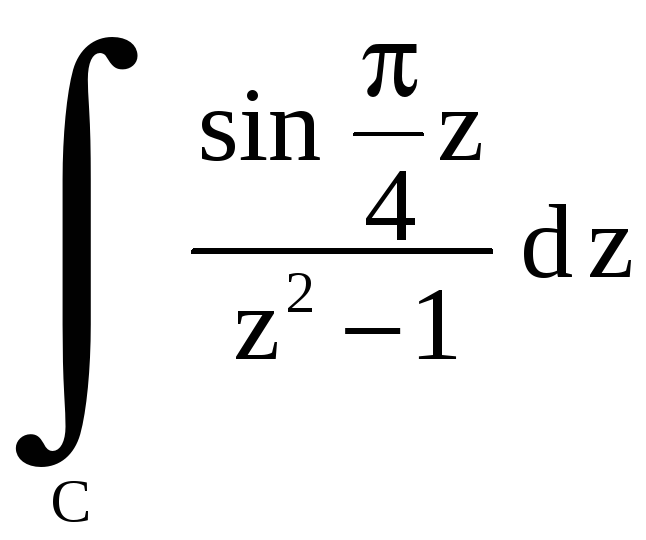 ,
где
,
где
![]() .
.
3.9.
Вычислить
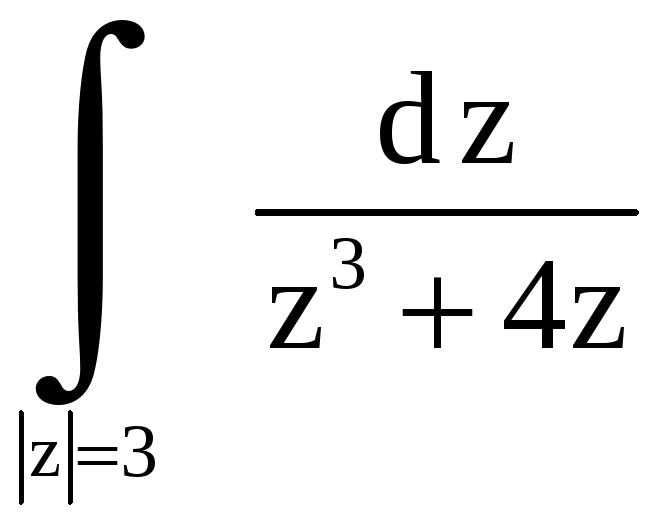 .
.
3.10.
Вычислить
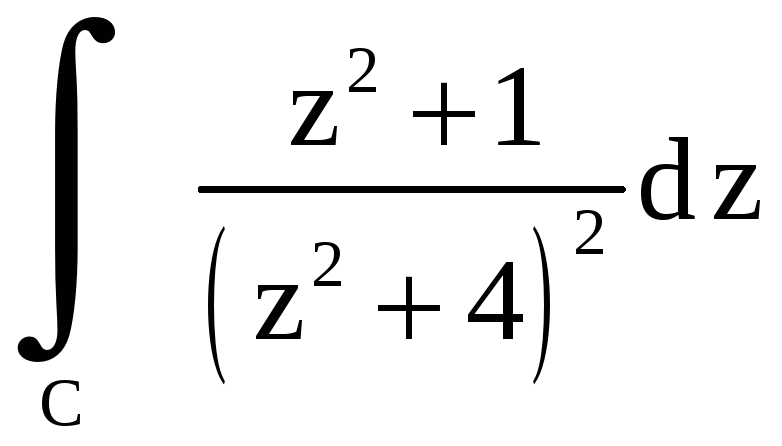 ,
где а)
,
где а)
![]() ;
б)
;
б)
![]() .
.
3.11.
Вычислить
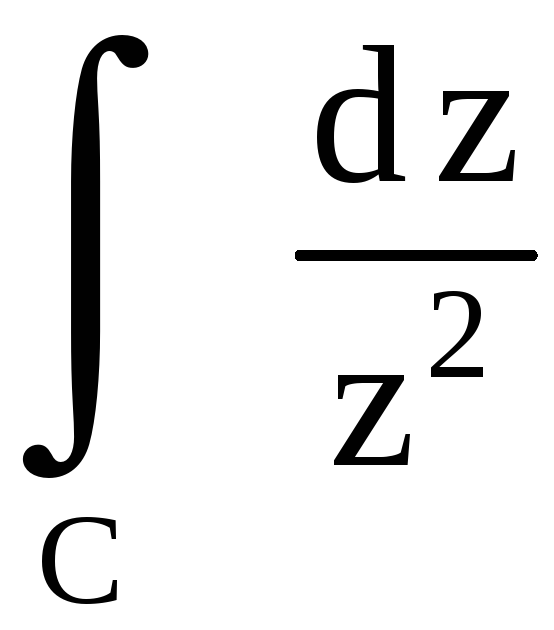 ,
где
,
где
![]() – окружность
– окружность
![]() .
.
3.12.
Вычислить
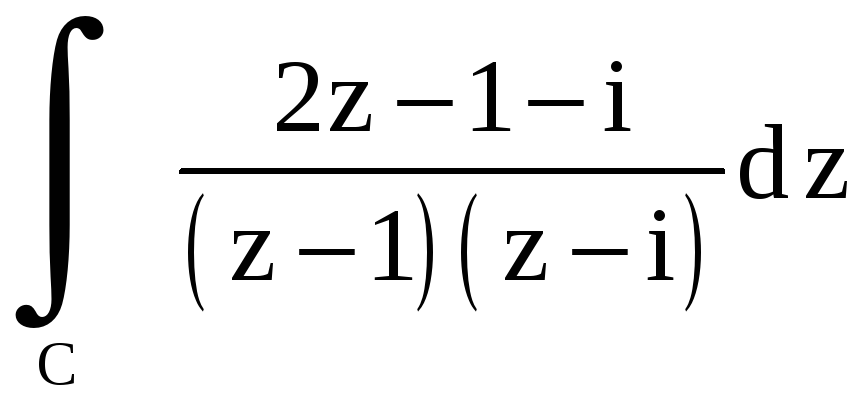 ,
где
,
где
![]() – окружность
– окружность
![]() .
.
3.13.
Вычислить
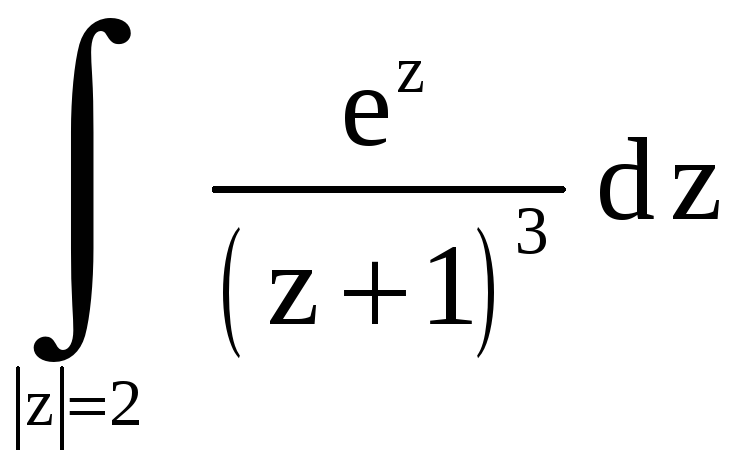 .
.

 y
y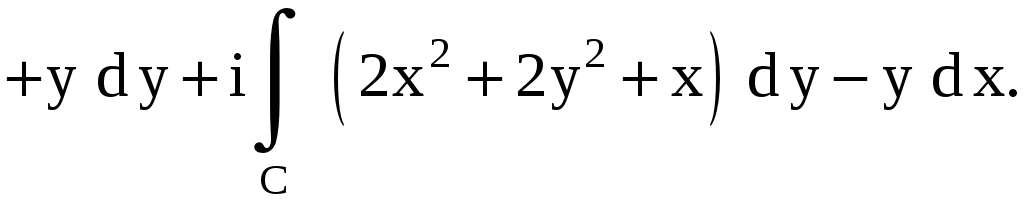
 y
y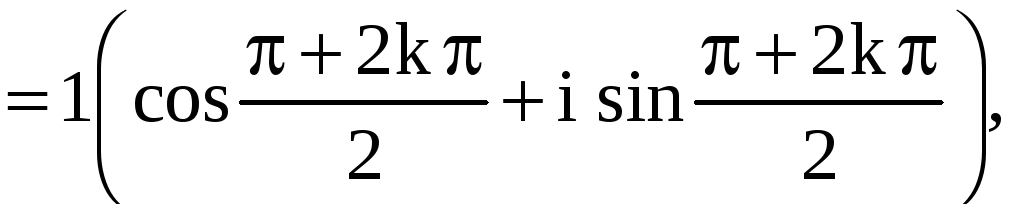
 y
y y
y y
y y
y
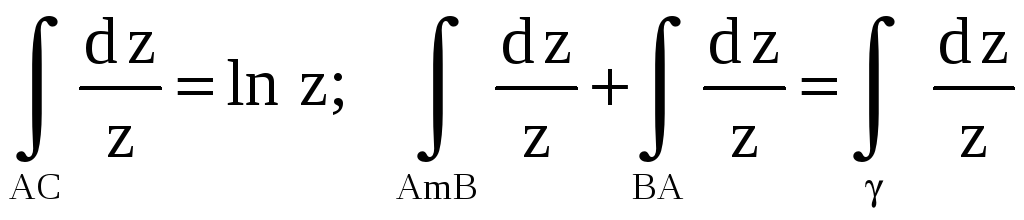 (рис.14);
(рис.14); ,
где
,
где
 y
y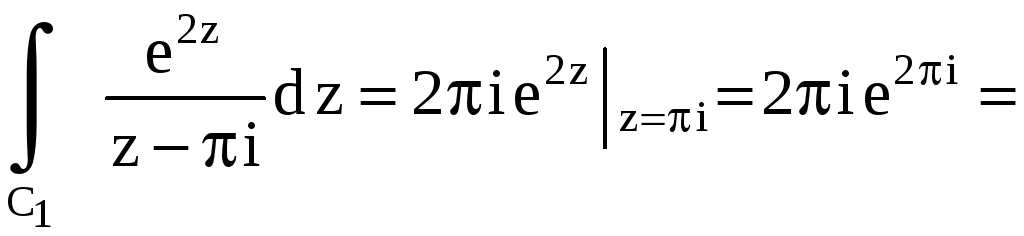
 y
y 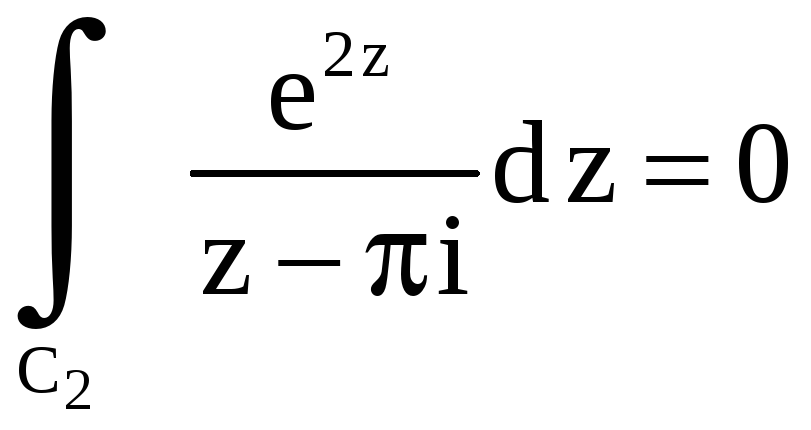 .
.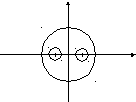
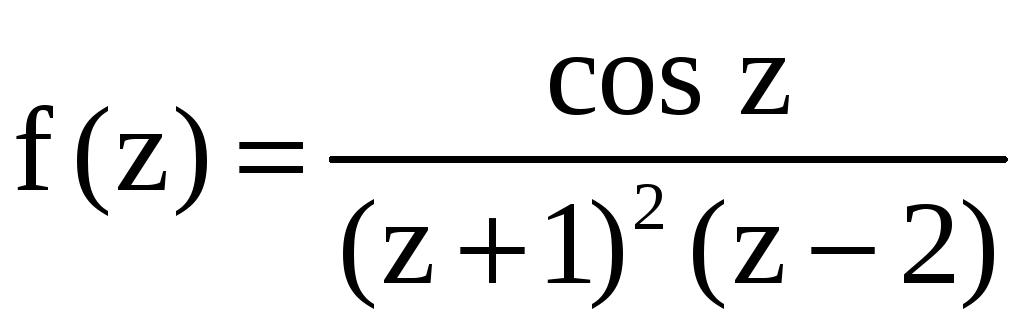 аналитична везде, кроме точек
аналитична везде, кроме точек