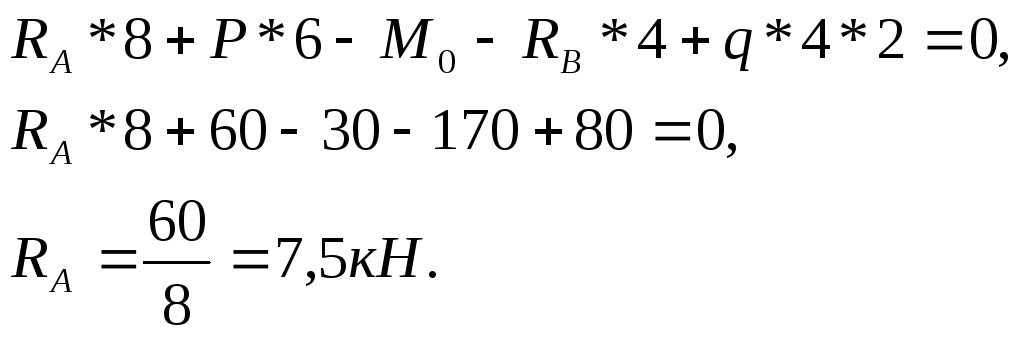Эпюра м(х).
Участок №1: ![]() Уравнение для
Уравнение для
![]()
(слева)
![]() -
(уравнение наклонной прямой)
-
(уравнение наклонной прямой)
x1=0: М(x1)= 0,
x1=3:
М(x1)=![]() = 42кНм.
= 42кНм.
Участок №2: ![]() Уравнение для
Уравнение для
![]()
(слева)
![]() -
(уравнение параболы)
-
(уравнение параболы)
Для построения параболы найдем три точки
X2=0:
М(x2)=
![]() кНм,
кНм,
X2=4:
М(x2)=
![]() .
.
Для определения третьей точки параболы воспользуемся дифференциальной зависимостью:

Подставим значение координаты Х20=1,9м в уравнение для М(х2) и найдем экстремальное значение изгибающего момента на данном участке (в нашем случае- максимум, т. к. вторая производная от М(х2)-отрицательна)
![]()
По правилу «зонтика»- парабола выпуклостью вверх.
Участок №3: ![]() Уравнение для
Уравнение для
![]()
(справа)
![]() -
(уравнение наклонной прямой)
-
(уравнение наклонной прямой)
x3=0: М(x3)= 0,
x3=2:
М(x3)=
![]() = 63 кНм.
= 63 кНм.
В точке приложения сосредоточенного момента Мо=25 кНм. На эпюре М(х) будет наблюдаться скачок, равный величине этого момента.
Условие прочности:
![]()
Максимальный изгибающий момент с М(х)
![]()
Момент сопротивления
для прямоугольного сечения:
![]() .
.
![]()
Из условия прочности
![]() откуда
откуда

![]()
Задача №3.
Дано:
Проверка
Эпюра Q(x)
Участок №1:
(слева)
параллельная оси
Х
x1=0:
Q(x1)=
P2=
5 кН,
x1=2:
Q(x1)=
P2=
5кН.
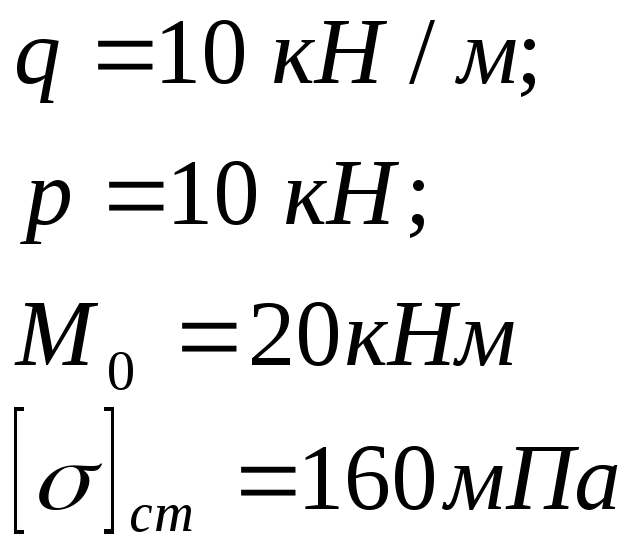
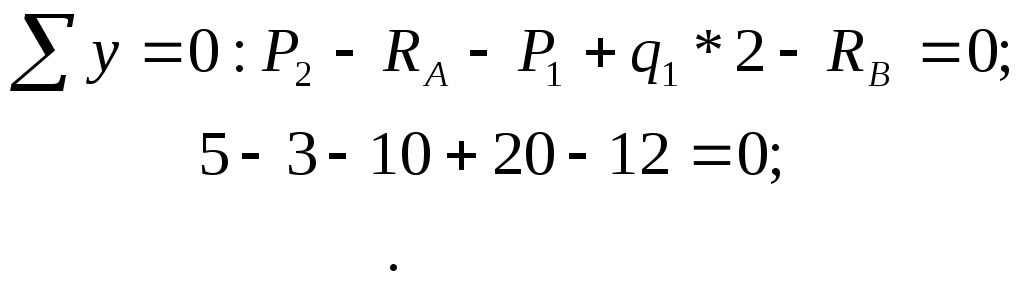
![]() Уравнение для
Уравнение для
![]()
![]() -
не зависит от Х1
, прямая
-
не зависит от Х1
, прямая
Составим уравнения статики:
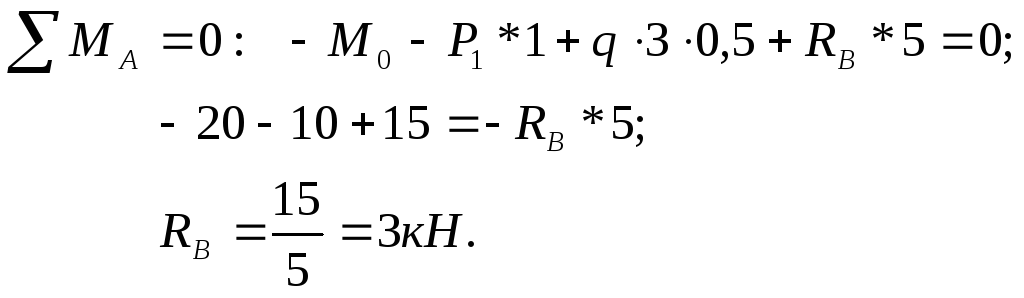
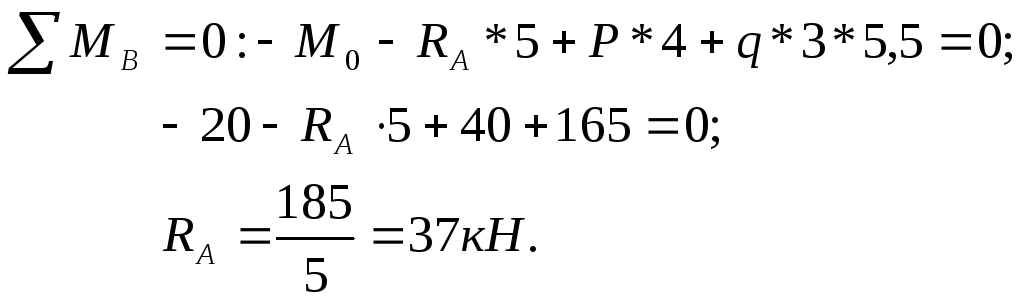
Проверка
![]()
Величина и направление реакции опор
определены правильно.
Эпюра Q(x)
Участок №1: ![]() Уравнение для
Уравнение для
![]()
(слева)
![]() -
уравнение наклонной прямой
-
уравнение наклонной прямой
Х1=0;Q(x1)=0
X1=2;Q(х1)=-q*2=-20кН
Участок №2: ![]() Уравнение для
Уравнение для
![]()
(слева)
![]() -
уравнение
наклонной прямой
-
уравнение
наклонной прямой
x2=0:
Q(x2)=
![]() =
17кН,
=
17кН,
x2=1:
Q(x2)=
![]() = 7кН.
= 7кН.
В точке приложения реакции опоры RA=37кН,
на эпюре Q(x) будет наблюдаться скачок,
равный величине этой реакции.
Участок №3: ![]() Уравнение для
Уравнение для
![]()
(справа)
![]() -не
зависит от x
-не
зависит от x![]() -
прямая, параллельная оси x.
-
прямая, параллельная оси x.
x3=0; Q(x3)=-RB =-3кH;
x3=4; Q(x3)= -RB=-3кН.
В точке приложения сосредоточенной силы Р1=10кН на эпюре Q(x) будет наблюдаться скачок равный величине этой силы.
Эпюра м(х).
Участок №1: ![]() Уравнение для
Уравнение для
![]()
(слева)
![]() -
уравнение
параболы
-
уравнение
параболы
x1=2:
М(x1)=![]()
По правилу «зонтика»- парабола выпуклостью вверх.
Участок №2: ![]() Уравнение для
Уравнение для
![]()
(слева)
![]() -
уравнение
параболы
-
уравнение
параболы
X2=0;
М(x2)
=
![]() кНм,
кНм,
X2=1;
М(x2)=
![]() .
.
По правилу «зонтика»- парабола выпуклостью вверх.
Участок №3: ![]() Уравнение для
Уравнение для
![]()
(справа)
![]() -
уравнение
наклонной прямой
-
уравнение
наклонной прямой
x3=0;
М(x3)=
-М EMBED Equation.3
![]() =-20кНм,
=-20кНм,
x3=4;
М(x3)=
-М EMBED Equation.3
![]() +RB
*4 EMBED
Equation.3
+RB
*4 EMBED
Equation.3
![]() = -8кНм.
= -8кНм.
Условие прочности:
EMBED
Equation.3
![]()
Максимальный изгибающий момент с М(х)
EMBED Equation.3
![]()
Из условия прочности
EMBED Equation.3
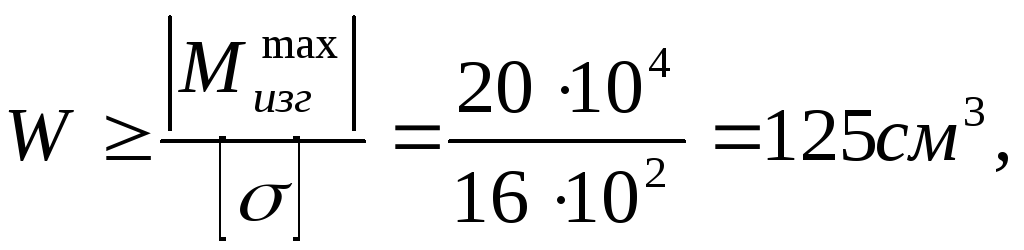
Из таблицы
стандартных профилей находим ближайшее
большее к расчетному значение EMBED
Equation.3
![]() ,
т.к. ближайшее меньшее W=109см
EMBED Equation.3
,
т.к. ближайшее меньшее W=109см
EMBED Equation.3
![]() не
удовлетворяет условию: EMBED Equation.3
не
удовлетворяет условию: EMBED Equation.3
![]() .
.
Выбираем двутавр №18.
Задача №4
Дано:
Определяем
неизвестные реакции опор, составляя
уравнения равновесия статики. Так как
неизвестных реакций три, то для
составления третьего уравнения
воспользуемся тем свойством, что момент
в шарнире «с» равен нулю.
1.
2.
3.
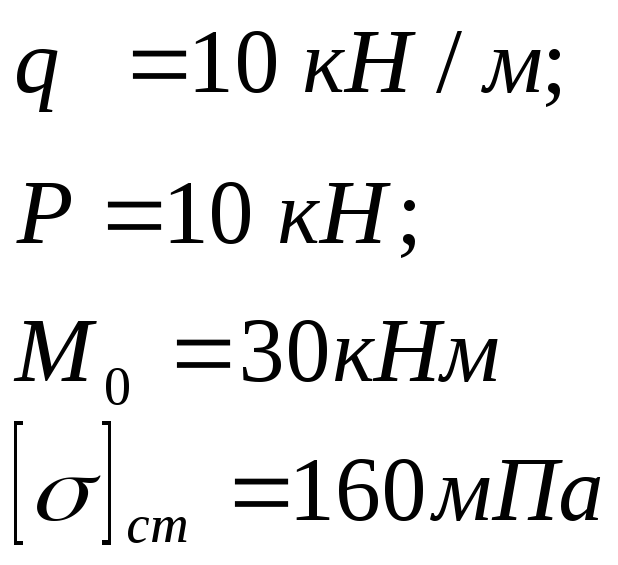
![]()
![]()
![]()
![]()
Подставим значение
EMBED Equation.3
![]() в
уравнение (1), находим значение RB
в
уравнение (1), находим значение RB
EMBED Equation.3
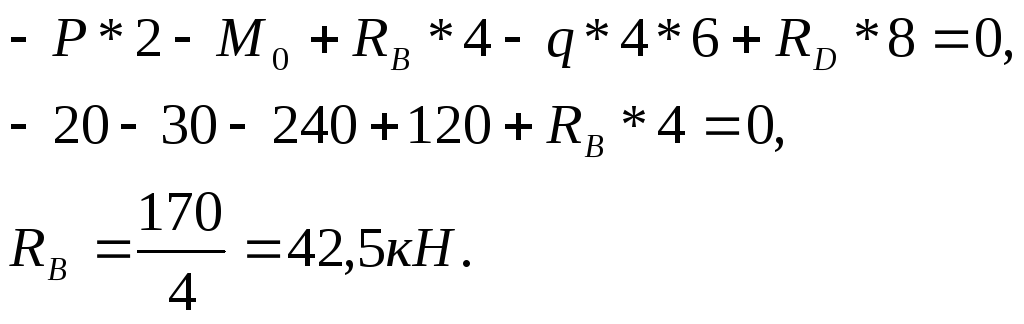
Подставим значение RB в (2), вычислим RA
EMBED Equation.3