
Министерство образования Российской Федерации
Санкт-Петербургский государственный горный институт
(Технический Университет)
Кафедра механики
Расчётно-графическая работа № 2
Дисциплина: Сопротивление материалов.
Тема: Построение эпюр перерывающих и изгибающих моментов
и подбор сечения балок.
Вариант №22
Выполнил: студент группы ГГ-01 _____________ / Цветкова Э.Э./
Проверил: профессор _____________ /Яковлев А.А./
Санкт-Петербург
2004г.
Задача №1.
Поскольку опора
представляет собой защемление (заделку),
то реакции этой опоры (R![]() ,M
,M![]() )
можно не определять. Они получаются
автоматически при построении эпюр
перерезывающих сил и изгибающих моментов.
Правила знаков при построении эпюр
перерезывающих сил и изгибающих моментов.
)
можно не определять. Они получаются
автоматически при построении эпюр
перерезывающих сил и изгибающих моментов.
Правила знаков при построении эпюр
перерезывающих сил и изгибающих моментов.
Правила знаков при построении эпюр:
перерезывающая
сила (слева):
![]()
изгибающий момент
(слева): (
![]() )
)
![]()
Дано:
Будем рассматривать
сечения по длине балки:- слева.
Участок
№1:
(слева)
На данном участке
поперечные силы отсутствуют. Поэтому
эпюрой перерезывающих сил является
ось X,
т.е.
Участок №2:
(слева)
x2=0:
Q(x2)=-P=-10
кН,
x2=4:
Q(x2)=-Р=-10
кН
Эпюра q(X)
![]() Уравнение для
Уравнение для
![]()
![]()
![]() Уравнение для
Уравнение для
![]()
![]() -
(не зависит от Х2-прямая, параллельная
оси Х)
-
(не зависит от Х2-прямая, параллельная
оси Х)
ф
Участок №3:
![]() Уравнение
для Q
(x
Уравнение
для Q
(x![]() )
)
(слева)
Q(x![]() )
=-Р-q*x
)
=-Р-q*x![]() - уравнение наклонной прямой
- уравнение наклонной прямой
x![]() =0;
Q(x
=0;
Q(x![]() )
=-Р=-10кН
)
=-Р=-10кН
x![]() =4;
Q(x
=4;
Q(x![]() )=-Р-q*4=-50кН
)=-Р-q*4=-50кН
Проверка:
![]() ; -Р-q*4+R
; -Р-q*4+R![]() =0
; -10-40+50=0
=0
; -10-40+50=0
Эпюра м(х).
Участок №1: ![]() Уравнение для
Уравнение для
![]()
(слева)
На данном участке
моменты от внешних сил отсутствуют,
поэтому эпюрой изгибающих моментов
является ось X,
т.е. М(x![]() )=0.
)=0.
Участок №2: ![]() Уравнение для
Уравнение для
![]()
(слева)
![]() -
(уравнение наклонной прямой)
-
(уравнение наклонной прямой)
X2=0: М(x2) = 0,
X2=4: М(x2) = -P*4=-40кНм,
Участок №3:
![]() ;
Уравнение для М(x
;
Уравнение для М(x![]() )
)
М(x![]() )=
)=![]() -уравнение
параболы
-уравнение
параболы
x![]() =0
;
=0
;![]()
![]()
В точке приложения
сосредоточенного момента М![]() =30
кНм, на эпюре М(x)
, будет наблюдаться скачок, равный
величине этого момента.
=30
кНм, на эпюре М(x)
, будет наблюдаться скачок, равный
величине этого момента.
По правилу «зонтика»- парабола выпуклостью вверх.
Проверка:
![]()
Условие прочности:
![]()
Максимальный изгибающий момент с эпюры М (х):
![]()
Момент сопротивления
для круглого сечения:
![]() .
.
Из условия прочности:
![]() откуда
откуда
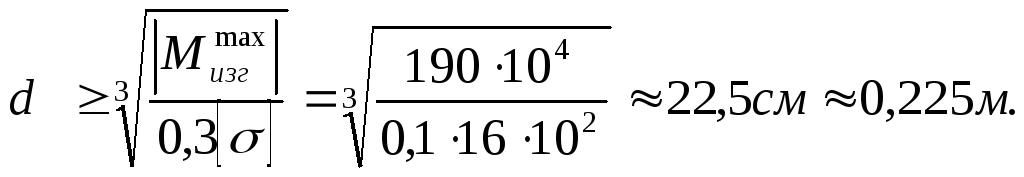
Задача№2
Дано:
Определяем
неизвестные реакции опор,
составляя
уравнения статики:
Проверка
Реакции опор
определены правильно.
Участок №1:
(слева)
x1=0:
Q(x1)=RA=
10,71
кН,
x1=2:
Q(x1)=
RA=10,71кН.
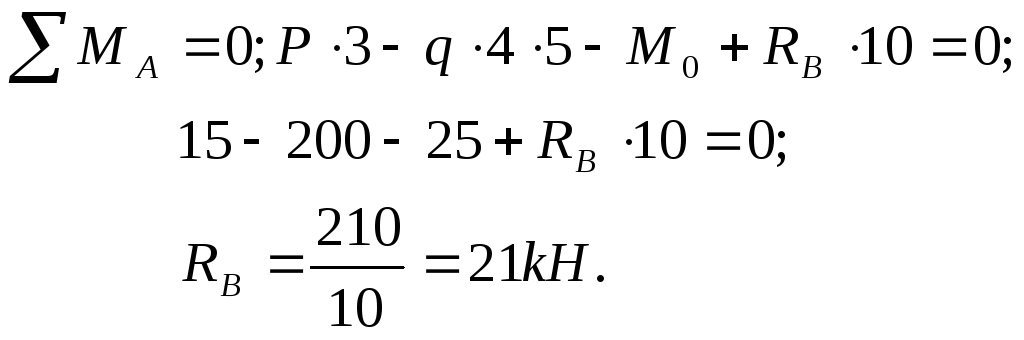
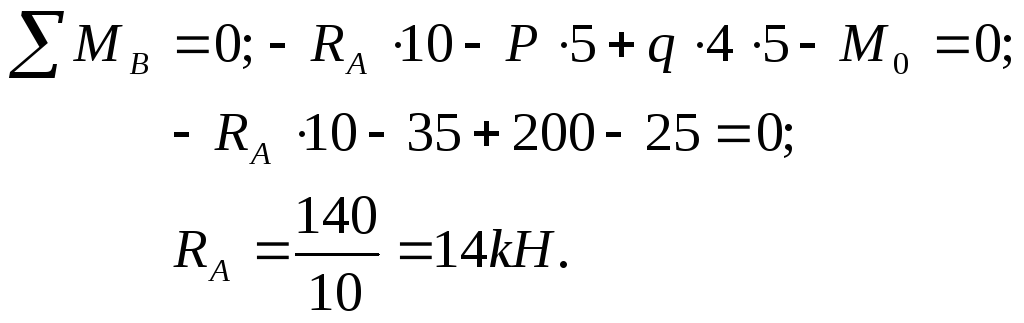
![]()
![]() Уравнение для
Уравнение для
![]()
![]() -
(не зависит от Х1,прямая,параллеоьная
оси Х)
-
(не зависит от Х1,прямая,параллеоьная
оси Х)
Задача №2. Эпюра q(X)
Участок №1:
![]() ; Уравнение для Q(x
; Уравнение для Q(x![]() )
)
(слева)
![]() -
не зависит от x
-
не зависит от x![]() -прямая,
параллельная оси x.
-прямая,
параллельная оси x.
![]()
Участок №2: ![]() Уравнение для
Уравнение для
![]()
(слева)
![]() -
(уравнение наклонной прямой)
-
(уравнение наклонной прямой)
x2=0: Q(x2)= RA+P=14+5 =19кН,
x2=4: Q(x2)= RA+P-q*4=14+5-40 = -21кН.
В точке приложения сосредоточенной силы Р=5 кН. На эпюре Q(х) будет наблюдаться скачок, равный величине этой силы. Эпюра Q (х2)пересекает ось Х, меняя знак с плюса на минус.
Найдем значение координаты Х20, при котором Q(X2)=0
![]()
![]()
Участок №3: ![]() Уравнение для
Уравнение для
![]()
(справа)
![]() -
(не зависит от Х3, прямая,
параллельная оси Х)
-
(не зависит от Х3, прямая,
параллельная оси Х)
x3=0: Q(x3)= -RВ = -21кН,
x3=2: Q(x3)= -RВ = -21кН.
