Содержание курса

 

Глава 8. Радиоастрономия и космология

8.1. Основные сведения о космологических моделях

8.2. Статистические подсчеты радиоисточников. Зависимость logN–logS

8.3. Реликтовое фоновое радиоизлучение

8.1. Основные сведения о космологических моделях

Основной наблюдательный параметр, имеющий отношение к крупномасштабной структуре Вселенной и к ее моделям – постоянная Хаббла H₀. Согласно закону Хаббла, для объектов на больших расстояниях их скорости удаления от наблюдателя пропорциональны расстояниям: v = H₀l. По современным определениям, большинство исследователей принимает величину H₀ = = 75 км/(с×Мпк). Обратная величина  = H₀^–1 = 1.3·10¹⁰ лет – “возраст” Вселенной (т.е. время, прошедшее с начала расширения, если расширение шло с постоянной скоростью).

Космологические модели описываются зависимостью масштабного фактора от времени R(t). Масштабный фактор вводится через величину четырехмерного линейного элемента

ds² = c²dt² – R²(t)du², (8.1)

du – элемент расстояния в сопутствующей трехмерной системе координат. Сопутствующей называется система, покоящаяся относительно вещества, находящегося в ближайшей окрестности. Введем сферическую систему координат (r, , ) с началом в некоторой точке, покоящейся относительно вещества. Тогда, при условии однородности и изотропности

(8.2)

где r – безразмерное расстояние, k – индекс кривизны. Индекс k принимает значения –1, 0, +1: k =–1 – Вселенная с отрицательной кривизной (двумерный аналог – седло или псевдосфера), k = 0 – плоская Вселенная (называемая также Вселенной Эйнштейна–де Ситтера), k = +1 – Вселенная с положительной кривизной (аналог – сфера).

Параметр R(t) характеризует "размер" Вселенной для данного момента времени t. Он входит в дифференциал расстояния dl между двумя наблюдателями, безразмерные радиальные координаты которых отличаются на dr:

при r << 1 l @ R(t)r. (8.3)

Если k = 0 и R(t) = const, то имеем плоское евклидово простран-ство.

Относительная скорость двух наблюдателей

(8.4)

т.е. выражается законом Хаббла.

Движение фотона в этой системе происходит по геодезической линии, которая определяется уравнением ds² = 0:

(8.5)

Если фотон излучается в отдаленной точке r_e в момент времени t_e, то он придет к наблюдателю, находящемуся в точке r = 0, в момент t₀. Момент t₀ определяется из уравнения геодезической

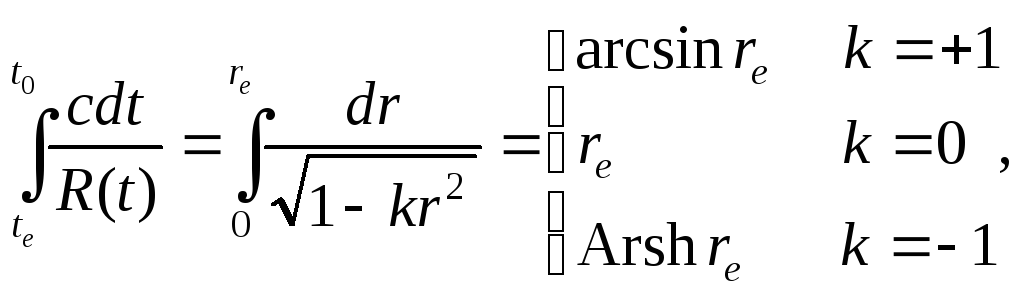(8.6)

где – обратная гиперболическая функция (ареа-синус). Таким образом, момент времени t₀ зависит только от r_e. Пусть наблюдаемый источник излучает монохроматическую волну и один гребень волны излучен в момент t_e, а следующий (через один период) – в момент t_e + t_e; первый гребень придет в точку r = 0 в момент t₀, а следующий – в момент t₀ + t₀. Из уравнения геодезической

(8.7)

Если за период волны R(t) не успеет заметно измениться, то

(8.8)

и изменение частоты фотона составит

(8.9)

Если R(t) растет со временем (Вселенная расширяется), то z > 0,  растет, и наблюдается красное смещение. Таким образом, красное смещение – естественное следствие эволюции Вселенной.

Эволюция фактора R(t) выводится из уравнений гравитационного поля. Предполагается, что известна средняя плотность вещества во Вселенной . Приведем без вывода некоторые соотношения

(8.10)

для настоящего момента времени

; (8.11)

индекс "0" означает величины, относящиеся к настоящему моменту времени. Величина

(8.12)

называется параметром замедления. В модели Эйнштейна–де Ситтера q₀= ½; для замкнутой Вселенной q₀ > ½; для открытой Вселенной q₀ < ½. Плотность вещества в современную эпоху

(8.13)

Критическая плотность (для случая q₀= ½)

(8.14)

при H₀ = 100h км/(с×Мпк).

По величине ₀ космологические модели делятся на открытые и закрытые. Критическое значение _cr ~ 1.9×10^–29h² г/см³ отделяет открытые модели (< _cr, q₀ < ½) от замкнутых (_cr, q₀ > ½). Зависимость фактора R(t) от времени в модели Эйнштейна–де Ситтера (q₀= ½)

(8.15)

При q₀ < ½ R(t) монотонно возрастает, причем по более быстрому закону, чем t^2/3. При q₀ > ½ функция R(t) вначале возрастает, проходит максимум, затем начинает уменьшаться – расширение сменяется сжатием. На рис. 8.1 представлены графики зависимости м

Рис. 8.1. Зависимость масштабного фактора от времени для разных типов космологических моделей.

асштабного фактора от времени для разных типов космологических моделей.

Итак, основные параметры, описывающие любую модель Вселенной – постоянная Хаббла H₀ и параметр замедления q₀.

Радиоастрономия позволяет наблюдать объекты, находящиеся на огромных расстояниях, где влияние переменности R(t) со временем становится существенным. Поэтому разработаны тесты, которые в принципе могут позволить сделать выбор в пользу той или иной космологической модели. Главный из них – подсчет числа радиоисточников в зависимости от плотности потока N(S).