4. Пульсары

Пульсары– источники пульсирующего р

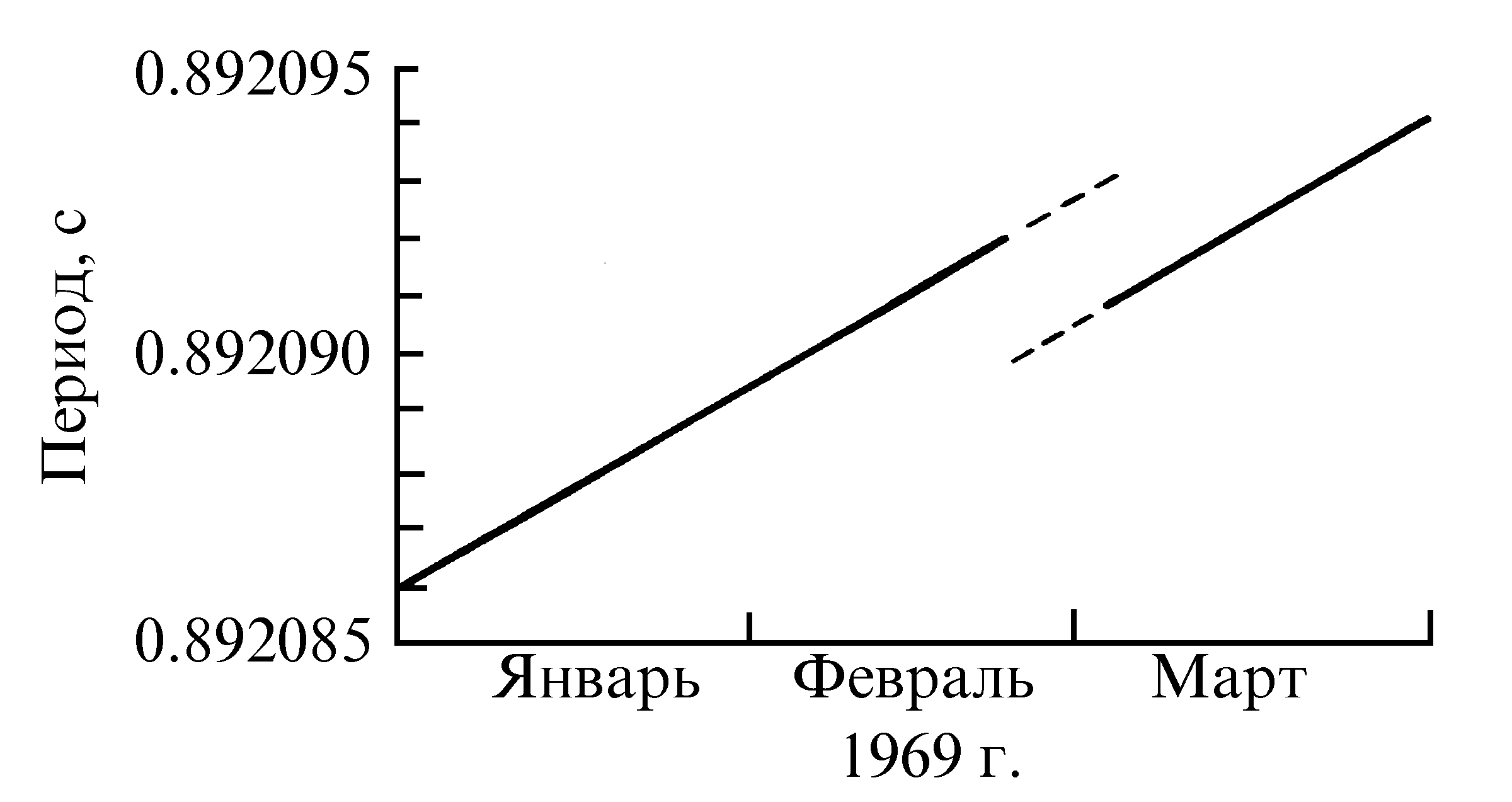
Рис. 6.8. Скачок периода пульсара Vela.

адиоизлучения. Это быстро вращающиеся нейтронные звезды, звездные остатки вспышек Сверхновых. Первые пульсары были открыты в 1967 г. К настоящему времени известно свыше тысячи пульсаров.

Пульсарное радиоизлучение поступает в виде правильно повторяющихся импульсов. Периоды повторения импульсов от ~1.5 мс до ~10 с. Стабильность повторения импульсов до 10^–9, но при этом у большинства пульсаров периоды со временем растут. Итак, два основных параметра любого пульсара – период следования импульсов P и производная периода . Время от времени у пульсаров наблюдаются сбои периода (glitches), когда период скачком уменьшается, а затем продолжает возрастать, но уже с несколько иной скоростью (рис. 6.8).

Скважность излучения от 10 до 100. Бывают интеримпульсы (то есть вторичные импульсы в промежутках между главными). Отдельные импульсы также могут обладать сложной внутренней структурой, которая может меняться от одного импульса к другому. Светимости радиопульсаров достигают 10³⁸ эрг/с.

Спектры пульсаров в диапазоне метровых волн (~ 100 – 400 МГц) линейные (S µ ^–), довольно крутые (в среднем  ~ ~ 3 ± 1), на частотах  > 1000 МГц наступает завал. Наблюдается сильная линейная поляризация излучения. В течение одного импульса происходит поворот плоскости поляризации. От импульса к импульсу свойства поляризации существенно меняются.

П

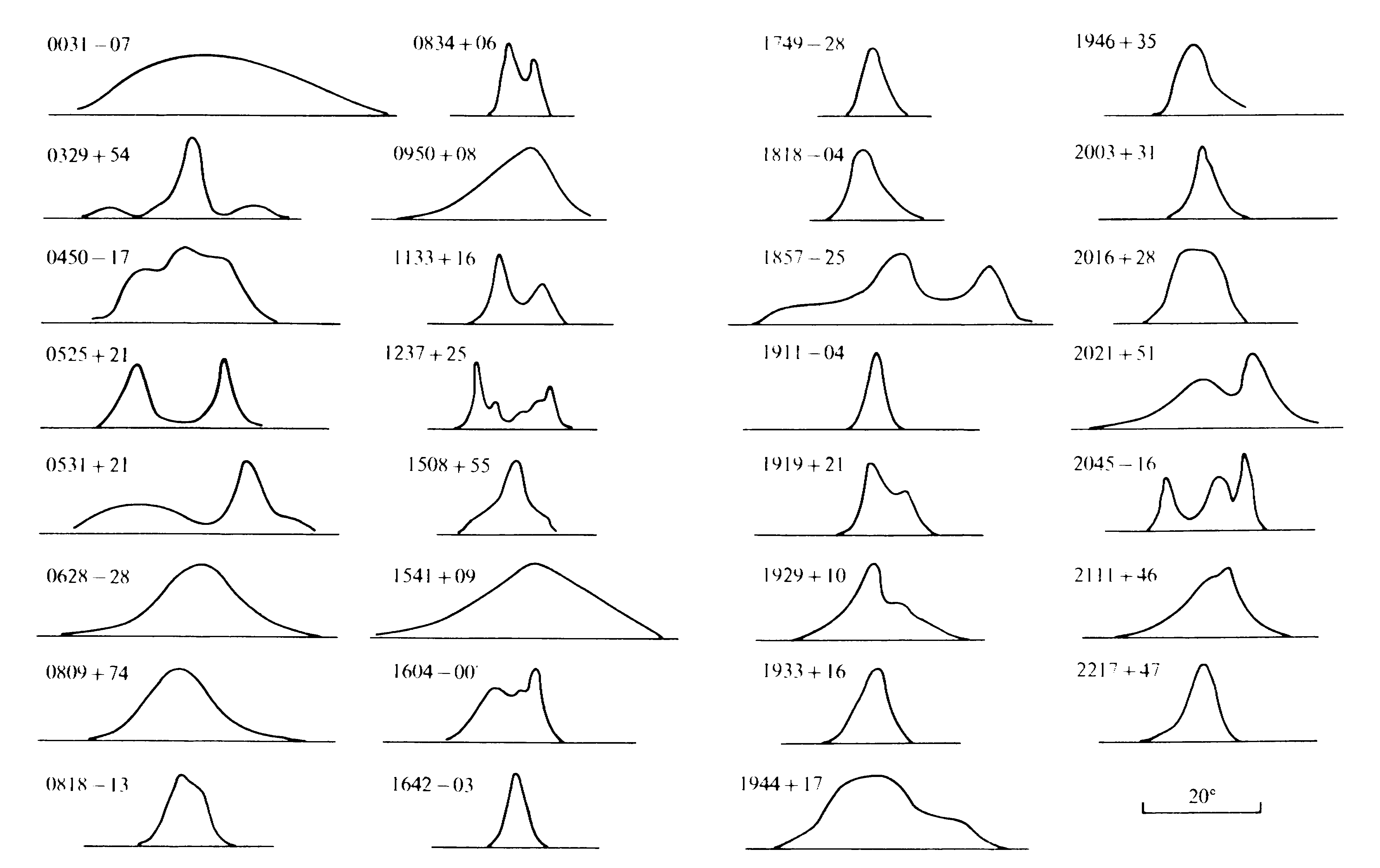
Рис. 6.9. Форма импульсов некоторых пульсаров.

ульсары интересны сами по себе. Но, благодаря уникальному характеру радиоизлучения в виде коротких импульсов широком диапазоне частот, они дают также возможность диагностики межзвездной среды на пути распространения сигнала к наблюдателю. Вследствие дисперсии радиоизлучения в слабоионизованной межзвездной среде запаздывание импульсов пульсара (по сравнению со временем L/c, L – расстояние до пульсара):

t =1.345×10^–3 ^–2 n_e L [с],

где  [Гц], n_e [см^–3], L [см], или

t = 4.15 (DM) ^–2 [с],

где  [МГц], DM [пк/см³].

Величина DM называется мерой дисперсии пульсара, она характеризует среднюю столбцовую плотность ионизованной среды в направлении пульсара и может использоваться для грубой оценки расстояния.

Излучение большинства пульсаров имеет линейную поляризацию. При прохождении ионизованной среды с магнитным полем плоскость поляризации испытывает фарадеевское вращение (из-за различия коэффициентов преломления для обыкновенной и необыкновенной волн, см. главу 2). Угол поворота плоскости поляризации

[рад] = (RM)² [рад], (6.9)

n_e [см^–3]; H_║ [мкГс] – продольная составляющая межзвездного магнитного поля (параллельная лучу зрения); l [пк];  [м]; RM [рад/м²] – мера вращения в межзвездной среде в направлении пульсара.

Наряду с периодом P и его производной , мера дисперсии DM и мера вращения RM – основные параметры пульсаров, определяемые непосредственно из наблюдений.

Простейший способ оценки возраста пульсаров использует свойство возрастания их периодов. Экстраполируем величину периода пульсара назад по времени к тому моменту, когда P = 0 (то есть считаем, что в момент рождения пульсар имел нулевой период). Тогда, очевидно, приближенный возраст пульсара  можно оценить как . Прокалибровать шкалу  можно по объектам, возраст которых известен из других данных. Пример такого объекта – пульсар в Крабовидной туманности, для которого точно известен момент рождения (вспышки Сверхновой) – 1054 год н.э. Оценка дает ~2000 лет. Поэтому обычно формулу для оценки возраста используют в виде

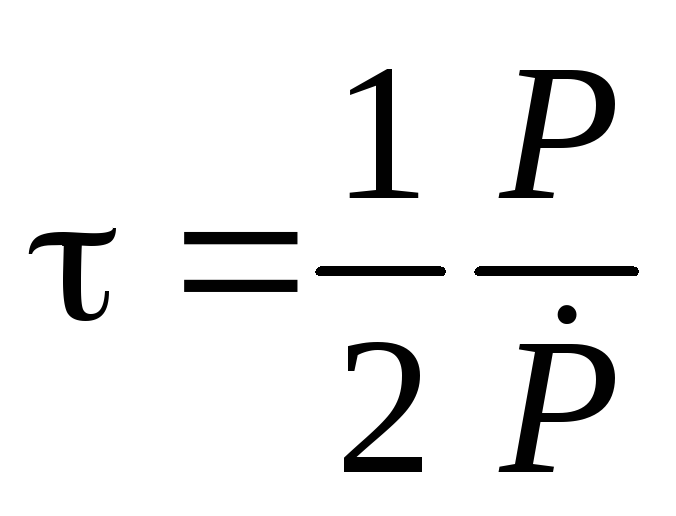, (6.10)

где ½ – "нормировочный множитель".

Оцененные по формуле (6.10) возрасты лежат в пределах 10⁶–10⁷ лет. Пульсар в Крабе – один из самых короткопериодических (P = 33 мс) и самых молодых ( ~ 950 лет). Относительно молод также пульсар Vela (P = 89 мс,  ~ 10⁴ лет).

Некоторые число пульсаров входит в двойные системы. Двойственность пульсара определяется по периодическим изменениям периода P пульсара. Один из пульсаров, входящих в двойную систему – PSR 1913+16. Период следования импульсов P = 59 мс, орбитальный период системы P_orb = 7^h45^m. Очень велик эксцентриситет орбиты: e = 0.61. Имеется смещение периастра со скоростью 3.6° в год и вековое уменьшение орбитального периода, что может свидетельствовать об излучении гравитационных волн. Таким образом, пульсары, входящие в двойные системы, предоставляют возможность проверки Общей теории относительности.

Имеется группа короткопериодических ("миллисекундных") пульсаров. Их периоды заключены в пределах от 1.5 до ~10 мс. Всего известно около пятидесяти миллисекундных пульсаров. По своим свойствам и эволюционному положению они сильно отличаются от "классических" пульсаров с более длинными периодами. У них производная периода < 10^–19, иногда даже отрицательна, магнитное поле ~10⁸ Гс, а возраст достигает 10⁹ лет. Практически обо всех миллисекундных пульсарах известно, что они входят в тесные двойные системы; в том числе – имеются пульсары в старых шаровых скоплениях. Двойственность дает ключ к пониманию их природы: это нейтронные звезды, испытавшие повторную "раскрутку" вследствие аккреции вещества с вторичного компонента, который уже достиг стадии красного гиганта и заполнил полость Роша.

У пульсара PSR B1257+12 по колебаниям периода обнаружены маломассивные спутники (0.2, 4.3 и 3.6 массы Земли), которые могут быть планетами, обращающимися вокруг пульсара.

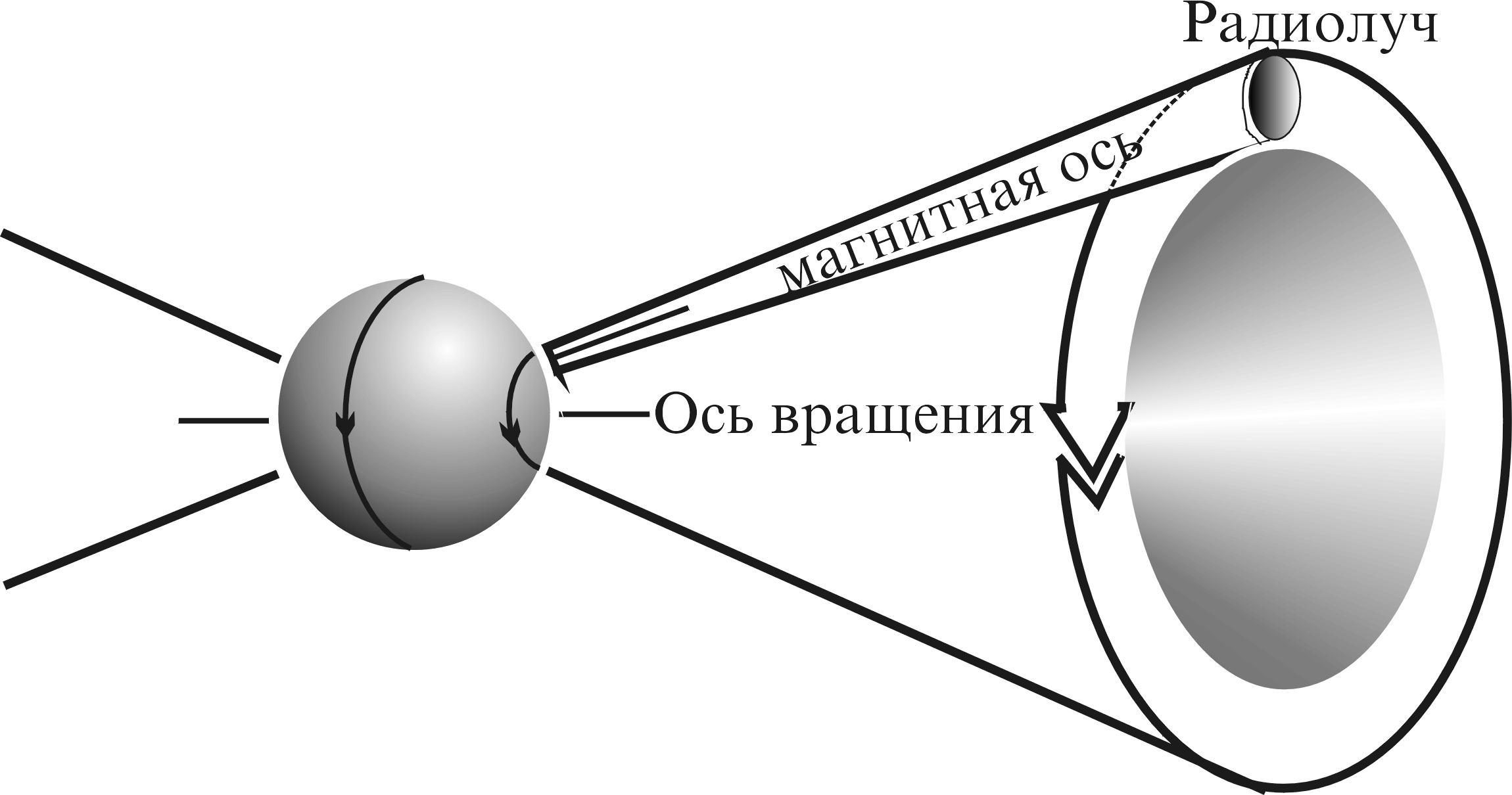
Модели пульсаров. Общепринятой является модель быстро вращающейся нейтронной звезды с сильным магнитным полем (~10¹² Гс). Поле имеет приблизительно дипольную структуру, магнитная ось, вообще говоря, не совпадает с осью вращения (рис. 6.10). Такой вращающийся диполь будет излучать волны на ч

Рис. 6.10. Модель радиоизлучения пульсара.

астоте вращения. Потеря вращательной энергии E вследствие магнитодипольного излучения

(6.11)

Здесь – энергия вращения, I – момент инерции нейтронной звезды,  – угловая скорость вращения, – период пульсара , m – компонент магнитного момента, перпендикулярный к оси вращения. Отсюда получим:

(6.12)

Масса и размер нейтронной звезды достаточно хорошо известны, а, следовательно, и момент инерции I. Отсюда можно найти магнитный момент и напряженность поля на поверхности нейтронной звезды (~10¹² Гс).

Следствие быстрого вращения магнитного поля – генерация сильного электрического поля в результате динамо-эффекта. Электрическое поле ускоряет заряженные частицы до очень высоких энергий.

Совместное вращение плазмы и магнитного поля возможно только внутри светового цилиндра (r = c/).

Ускоряемые частицы летят вдоль силовых линий. Излучение идет преимущественно в направлении движения. На Земле излучение принимается тогда, когда конус, в котором излучают частицы, направлен на Землю.

Предложены два типа моделей пульсаров:

1) излучение возникает вблизи поверхности светового цилиндра;

2) излучение возникает вблизи поверхности нейтронной звезды.

В моделях первого типа направленность излучения – следствие релятивистской тангенциальной скорости вращающейся плазмы вблизи поверхности светового цилиндра; частицы излучают при помощи синхротронного механизма.

В моделях второго типа имеет место излучение частиц, летящих вдоль силовых линий магнитного поля, в направлении вектора мгновенной скорости.

Сбои периода пульсаров (glitches) вызваны звездотрясениями, разломами в структуре нейтронной звезды. Разломы приводят к уменьшению момента инерции, а, следовательно, и периода. При этом достаточно очень малого изменения размера нейтронной звезды. Момент инерции сплошного шара массой M равен ; из формул вращательного движения имеем

(6.13)

При сбое периода пульсара в Крабе в сентябре 1969 г. было . При R = 10 км требуемое изменение радиуса R всего лишь 5 мкм. При звездотрясении, вероятно, происходит растрескивание коры нейтронной звезды, меняется момент инерции, однако нейтронную жидкость внутри звезды это очень мало затрагивает.

Массы нейтронных звезд M от 0.15 до 1.7. При массе >1.7образуется черная дыра. При M < 1звезда может быть и белым карликом, но при вспышке Сверхновой происходит существенная перестройка всей структуры звезды, и гораздо вероятнее образование именно нейтронной звезды (или черной дыры).

Структура нейтронной звезды (при радиусе R = 10 км): ядро радиусом 1 км – твердое, содержит только наиболее массивную нейтронную компоненту; далее до радиуса 9 км – "нейтронная жидкость", состоящая из смеси нейтронов, протонов и электронов; и внешняя кора толщиной 1 км, состоящая из тяжелых ядер.

При быстром вращении замагниченной нейтронной звезды возникает сильное электрическое поле:

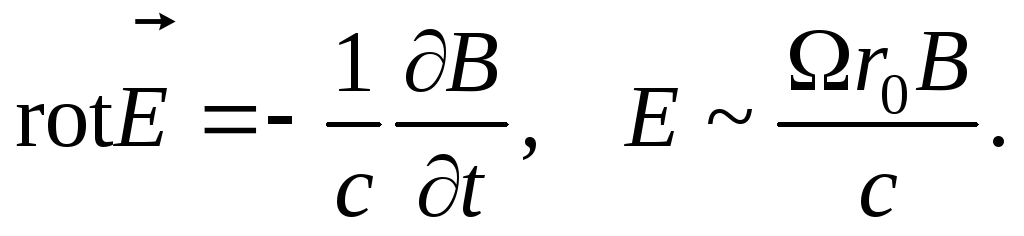(6.14)

Здесь r₀ – радиус светового цилиндра. Для пульсара в Крабе  = = 200 с^–1, B = 10¹² Гс, отсюда напряженность электрического поля ~10¹⁸ В/см, а разность потенциалов между полюсом и экватором ~10¹⁸ В. Следовательно, энергия ускоряемых частиц может достигать ~10¹⁸ эВ (если только поле не изменено экранирующим объемным электрическим зарядом). Таким образом, пульсары – важные источники космических лучей в Галактике. Однако трудность данной модели в том, что частицы, которые теряет звезда, приводят к появлению на ее поверхности заряда, который запирает дальнейшее вырывание частиц. Выход состоит в генерации электрон-позитронных пар в сильном магнитном поле -квантами синхротронного происхождения от первичных частиц.