Розділ 2: послідовності незалежних випробовувань. Формула бернуллі

Якщо досліди проводити послідовно один за одним в одних і тих же умовах, причому так, що ймовірність реалізації події А не залежить від наслідку інших випробувань, то такі випробування рахуються незалежними відносно подій А.

В подальшому будемо рахувати, що ймовірність події А в усіх випробовуваннях (спробах) одна і та ж.

Під складною подією будемо розуміти суміщення кількох подій, які будемо називати проектами.

Нехай приводиться „n” спроб отримати подію А, причому в кожній спробі ймовірність появи події „А” одна і та ж і рівна „p”. Ймовірність не реалізації події А буде q = 1 – p. Нехай необхідно дізнатися ймовірність отримати подію А „k” раз якщо здійснено „n” спроб.

Зрозуміло, що позитивна реалізація події А не повинна бути якоюсь певною. Шукану ймовірність можна обчислити по формулі Бернуллі.

Вивід формули Бернуллі:

Згідно теореми множення ймовірностей, якщо в „n” спробах реалізується „k” раз подія, то ймовірність однієї спроби даної ситуації обчислюється за формулою

P_n⁽¹⁾ (k) = p^k q^n-k

В даній формулі реалізується лише одна, певна послідовність виникання події А.

Наприклад 10001110... (тут k одиничок та n-k нулів)

Число комбінацій, які сприяють появі даного результату з ”n” спроб „k” позитивна реалізація події визначається:

C_n^k = n!/k! (n-k)!

Якщо допускається, що до мети (виникнення „k” помірних реалізацій при „n” спробах) веде довільна комбінація як така 1010101..., так і інша 001110… то згідно суми ймовірностей незалежних подій шукана ймовірність буде:

P_n(k) = C_n^k P^k q^n-k = 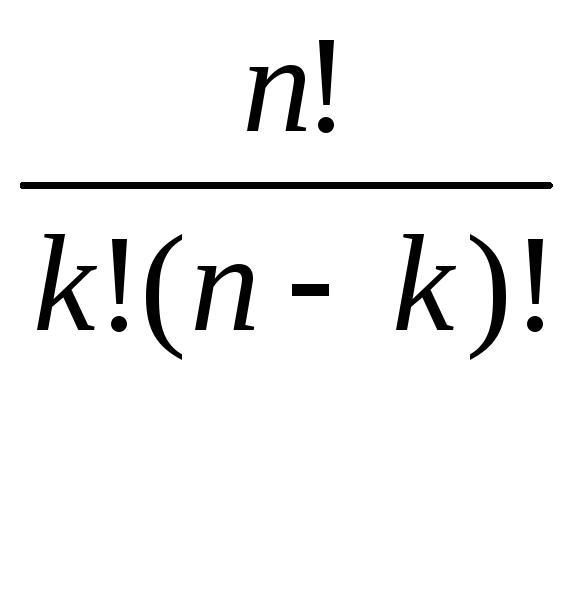P^k q^n-k (1)

Отримана формула називається формулою БЕРНУЛЛІ.

ПРИКЛАД: Ймовірність того, що на протязі доби екзаменаційні сесії двійок отримає не більше p = 0,1; Знайти ймовірність того, що за всю сесію (20 днів) на протязі 7 довільних днів отримало двійку не більше p = 0,1 студентів.

Ясно що при p = 0,1 a = 0,9 шукана ймовірність обчислюється за формулою:

P₂₀(7) = C₂₀⁷ P⁷ q^20-7 = 0,1⁷ 0,9¹³

Набір чисел k = 0,1,2,...,n називається біноміальним розподілом, а саму формулу

P_n(k) = C_n^k P^k q^n-k

біноміальною формулою.

Оскільки 1ⁿ = 1, то

(p + q)ⁿ = C_n^k P^k q^n-k = 1 (2)

Число настання події являється найімовірнішим, якщо ймовірність даної події більша, за усі інші. Ясно, що для різних „k” ймовірність буде різною. Якщо n число незалежних випробовувань, p – ймовірність настання даної події в одній спробі а

q = 1 – p – ймовірність не послання події, то найімовірніше число настання події „k₀” задовольняє нерівності :

(3)

Оскільки k_0­ – додатнє число, а різниця np + p – (nр – q) = p + q = 1, то завжди існує оптимальне значення k₀.

Поведінка функції біномного розподілу від „k” можна дослідити так:

Обчислимо відношення

= () для довільних k = 0,1,2,3,...,n

Ясно, що коли

> 1 – то ймовірність зростає.

Якщо ж

< 1 – то спадає.

Тоді

> 1 => pn – kp > kq + q,

pn – q > k (p + q), aле p + q = 1

Отже при k < pn – q ймовірність зростає.

Якщо ж k > pn – q, то функція буде спадати. Схематичний графік даної функції:

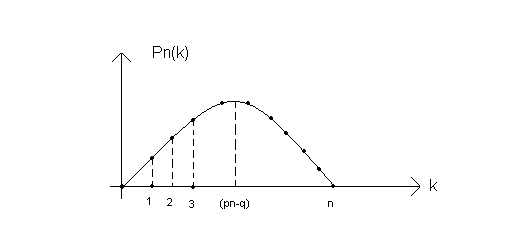
Як бачимо максимум обов’язково є.

Зрозуміло, що pn – q – не є цілим числом. Якщо врахувати однак , що k₀ є цілим числом, то , як виявляється k₀ мусить задовольняти нерівності .

Якщо ймовірність „p” одного порядку з величиною (1/n) при великих „n” або при

Р< 0,1 то обчислення згідно формули (1) можна здійснити спрощеним чином

(4)

де λ= n p

Необхідність заміни (1) на (4) виникає досить часто у випадках великого числа n, адже значно складніше проводити обчислення n!.

Формула (4) називається розподілом Пуассона. Даний розподіл є в таблицях.

Наприклад: На факультеті є близько 500 студентів. Яка ймовірність того, що 1-го вересня в 3-х студентів день народження. Ймовірність того, що в одного студента день народження 1-го вересня P = (365 днів у році); згідно (4) p n = = λ= 1,37 .

Тоді шукана ймовірність буде.

Спроба провести дані обчислення за допомогою (1) привела б до необхідності обчислення великих чисел, порядку 365!.

Що ж робити у тому випадку коли порушуються умови застосування формули Пуассона? Якщо, наприклад, p=0.4.