Указания к выполнению контрольной работы №1 Примеры решения задач.

I. Элементы линейной алгебры и аналитической геометрии.

Пример 1. Даны векторы ₁(2 ; 4 ; 3 ; 2), ₂(4 ; 2 ; 2 ; 8), ₃(4 ; 5 ; 8 ; 7), ₄(6 ; 7 ; 5 ; 3) и (18 ; 24 ; 13 ; 6). Показать, что векторы ₁, ₂, ₃, ₄ образуют базис четырехмерного линейного пространства R₄ и найти координаты вектора в этом базисе.

Решение.

Выражение х₁+₁+х₂₂+…+х_кк называется линейной комбинацией векторов ₁, ₂, …_к с коэффициентами х₁, х₂, …х_к. Любая линейная комбинация векторов линейного пространства представляет собой вектор того же пространства. Если некоторый вектор _{линейного пространства представлен в виде линейной комбинации векторов 1},…, _к того же пространства, т.е.

(1)

то говорят, что вектор разложен по векторам ₁,…_к Система векторов ₁, ₂, …_к некоторого линейного пространства называется линейно независимым, если равенство

(2)

имеет место только при нулевых значениях коэффициентов х₁, х₂, … , х_к, если же равенство (2) выполняется и при условии, что хотя бы один из коэффициентов х₁, х₂, … , х_к, отличен от нуля, то система векторов ₁, ₂, …_к называется линейно зависимой.

Для векторов с заданными координатами ₁(х₁, y₁, z₁, p₁), ₂(x₂, y₂, z₂, p₂), ₃(x₃, y₃, z₃, p₃), ₄(x₄, y₄, z₄, p₄), составим определитель и вычислим его.

(3)

Подставим в (3) данные векторы 1, 2, 3, 4 , получим

Так как , то векторы линейно независимы и они образуют базис линейного пространства R₄ . Для вычисления координат вектора в этом базисе составим систему линейных уравнений из координат векторов ₁, ₂, ₃, ₄ и и решим ее методом Гаусса:

*

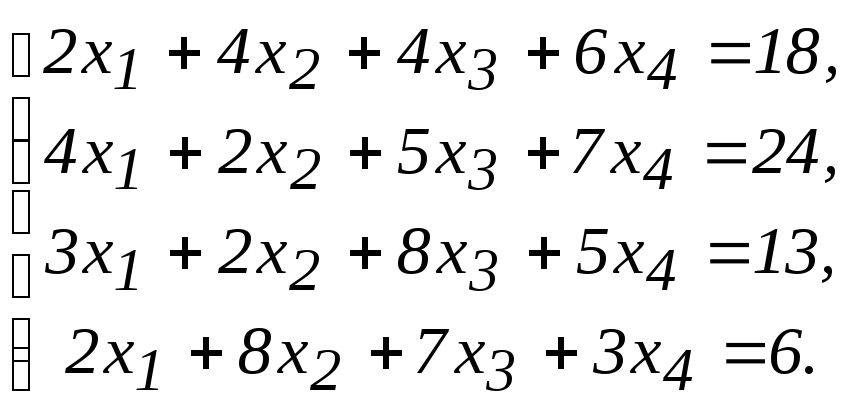Составим матрицу системы и преобразуем ее к треугольному виду, т.е. будем последовательно получать нули ниже главной диагонали матрицы, на которых находятся элементы 2, 2, 8, 3.

Разделим каждый элемент I строки на 2, затем полученную I строку умножим последовательно на -4; -3; -2 и сложим соответственно со II; III и IV строками, получим:

~

Разделим III строку на (-2) и поменяем ее местами со II строкой.

Новую II строку умножим последовательно на 3; -2 и сложим соответственно с III и IV строками, получим:

III строку умножим на 5, IV на 6 и сложим их, получим:

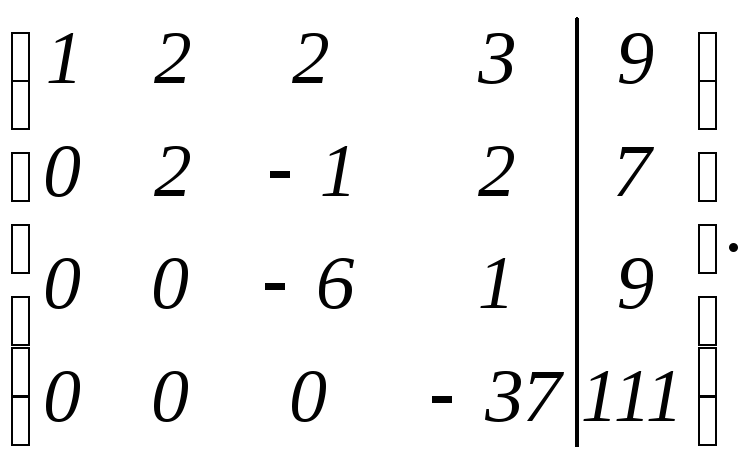
Таким образом получим матрицу ступенчатого вида, например х₁, х₂, х₃, х₄,

откуда х₄ = 3, х₃ = -1, х₂ = 0, х₁ = 2.

Решение системы * (2; 0; -1; 3) образует совокупность координат вектора в базисе ₁, ₂, ₃, ₄ , т.е. в этом базисе (2; 0; -1; 3) или = 2₁ -₃ + 3₄.

Пример 2. Даны координаты вершин пирамиды А₁(2; 1; 0), А₂(3; -1; 2), А₃(13; 3; 10), А₄(0; 1; 4).

Найти: 1) длину ребра А₁А₂;

2) угол между ребрами А₁А₂ и А₁А₄;

3) угол между ребрами А₁А₄ и гранью А₁ А₂ А₃;

4) площадь грани А₁ А₂ А₃;

5) объем пирамиды;

6) уравнение прямой А₁А₂;

7) уравнение плоскости А₁ А₂ А₃;

8) уравнение высоты, опущенной из вершины А₄ на грань А₁ А₂ А₃ . Сделать чертеж.

Решение.

1) Расстояние d между точками А(х₁, y₁, z₁) и В(х₂, y₂, z₂), определяется по формуле

(1)

Подставим в (1) координаты точек А₁ и А₂ , находим длину ребра А₁А₂:

А₁А₂=

2) Угол между ребрами А₁А₂ и А₁А₄ равен углу φ между направляющими векторами этих ребер и . Косинус угла между двумя векторами = скалярному произведению этих векторов, деленному на произведение их модулей:

(2)

Координаты вектора с началом в точке А₁(x₁, y₁, z₁) и концом в точке А₂(x₂, y₂, z₂)

(3)

Применяя (3), получим (1; -2; 2), (-2; 0; 4). Применяя (1), получим модули векторов

Скалярное произведение двух векторов с заданными координатами равны сумме произведений соответствующих координат, т.е если (а₁, а₂, а₃), (), то их скалярное произведение

(4)

Применяя (4), найдем . Следовательно,

3) Угол между ребром А₁А₄ и гранью А₁ А₂ А₃ равен углу φ между направляющим вектором данного ребра и нормальным вектором плоскости А₁ А₂ А₃ .

Уравнение плоскости, проходящей через 3 данные точки А₁(х₁, y₁, z₁) и А₂(х₂, y₂, z₂), А₃(х₃, y₃, z₃) имеет вид

(5)

Подставим в (5) координаты точек А₁ А₂ А₃, получим:

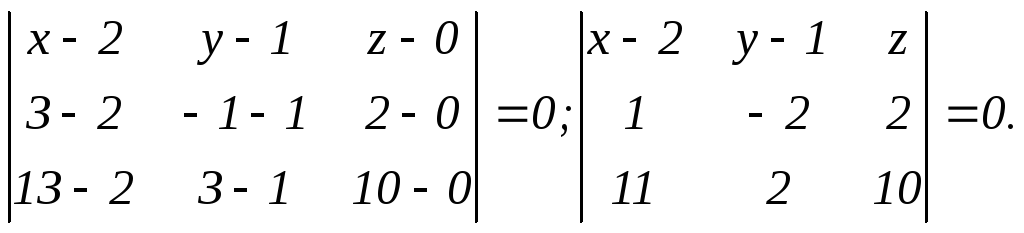
Разложим определитель по элементам I строки:

Сократив на (-12), получим уравнение плоскости А₁ А₂ А₃ :

2x – 4 – y + 1 - 2z = 0

2x – y - 2z – 3 = 0

Если уравнение плоскости α задано в каноническом виде Ax + By + Cz + Д = 0, то ее нормальный вектор _α (А; В; С), т.е. нормальный вектор плоскости А₁ А₂ А₃ имеет координаты (2; -1; -2). Синус угла α между вектором и плоскостью А₁ А₂ А₃

(6)

Найдем скалярное произведение по формуле (4):

_{= -2 2 + 0 (-1) + 4 (-2) = - 4 – 8 = -12.}