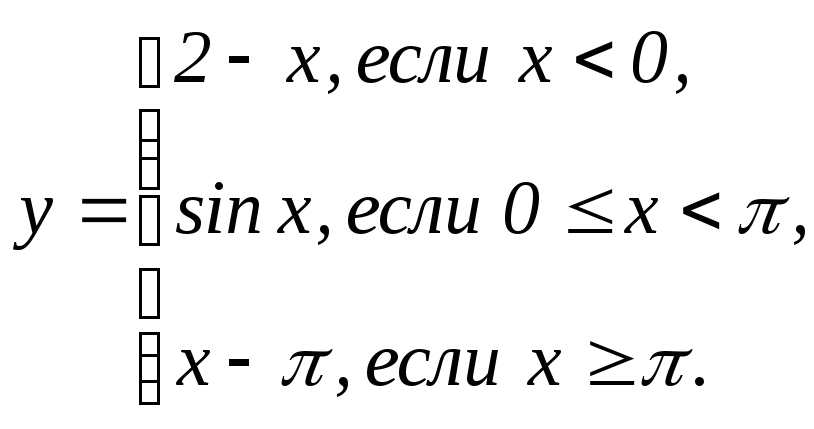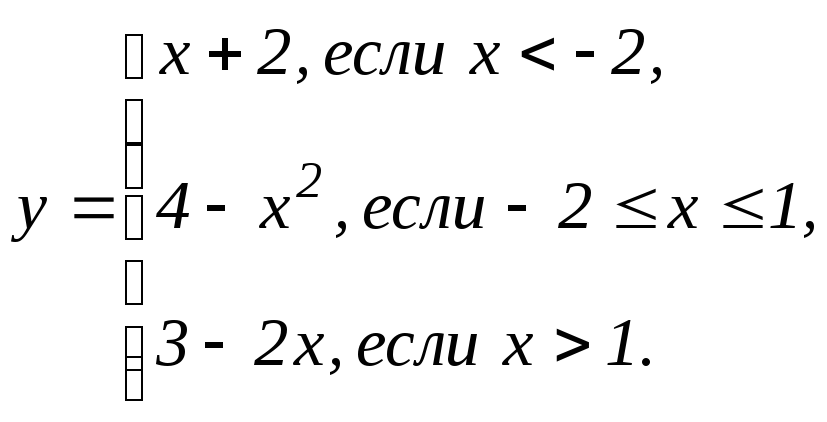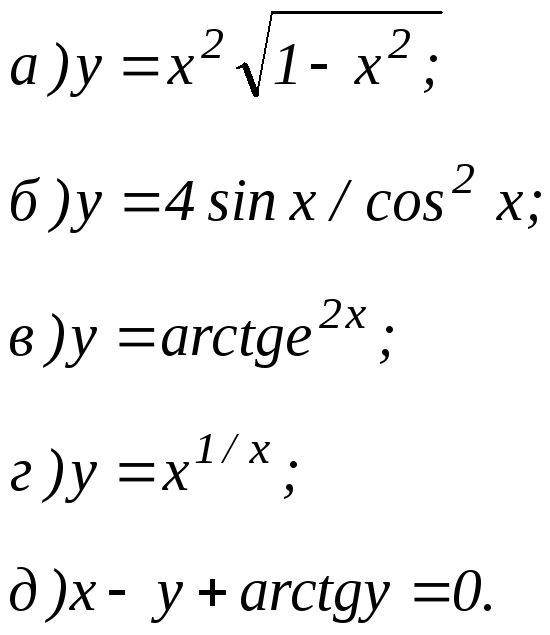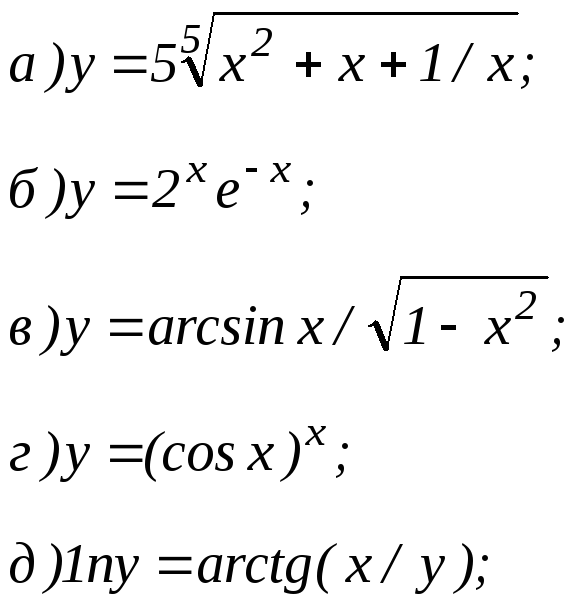- •Высшая математика методические указания и контрольные задания
- •Задания для контрольных работ по математике для студентов заочной формы обучения
- •Указания к выполнению контрольной работы №1 Примеры решения задач.
- •I. Элементы линейной алгебры и аналитической геометрии.
- •Подставим в (3) данные векторы 1, 2, 3, 4 , получим
- •Применяя формулу (1), получим
- •Если определитель системы уравнений то такая система уравнений имеет одно определенное решение, получаемое по формулам
- •Ιι. Введение в матаматический анализ
- •III. Производная и ее приложения
- •Формула Тейлора
- •IV. Функции нескольких переменных
- •V. Неопределенный и определенный интегралы.
- •Определенный интеграл
- •Числовые ряды
- •Знакопеременные ряды
- •Функциональные и степенные ряды
- •Ряды Фурье
- •Уравнение математической физики Решение уравнения колебания струны методом характеристик (методом Даламбера)
- •Элементы операционного исчисления
- •Теория вероятностей и математическая статистика
- •Контрольные задания
Задания для контрольных работ по математике для студентов заочной формы обучения
Контрольная работа №1
1 - 10. Даны векторы а (а1; а2; а3), b (b1; b2; b3), с (с1; с2; с3) и d (d1; d2; d3) в некотором базисе. Показать, что векторы а, b, c образуют базис, и найти координаты вектора d в этом базисе.
-
а (1;2;3), b (-1;3;2), с (7;-3;5), d (6;10;17).
-
а (4;7;8), b (9;1;3), с (2;-4;1), d (1;-13;-13).
-
а (8;2;3), b (4;6;10), с (3;-2;1), d (7;4;11).
-
а (10;3;1), b (1;4;2), с (3;9;2), d (19;30;7).
-
а (2;4;1), b (1;3;6), с (5;3;1), d (24;20;6).
-
а (1;7;3), b (3;4;2), с (4;8;5), d (7;32;14).
-
а (1;-2;3), b (4;7;2), с (6;4;2), d (14;18;6).
-
а (1;4;3), b (6;8;5), с (3;1;4), d (21;18;33).
-
а (2;7;3), b (3;1;8), c (2;-7;4), d (16;14;27).
-
а (7;2;1), b (4;3;5), с (3;4;-2), d (2;-5;-13).
11 - 20. Даны координаты вершин пирамиды А1А2А3А4. Найти 1) длину ребра А1А2; 2) угол между ребром А1А2 и А1А4; 3) угол между ребрами А1А4 и гранью А1А2А3; 4)площадь грани А1А2А3; 5) объем пирамиды; 6) уравнение прямой А1А2; 7) уравнение плоскости А1А2А3; 8) уравнение высоты, опущенной из вершины А4 на грань А1А2А3. Сделать чертеж.
11. А1 (4;2;5), А2 (0;7;2), А3 (0;2;7), А4 (1;5;0).
-
А1 (4;4;10), А2 (4;10;2), А3 (2;8;4), А4 (9;6;4).
-
А1 (4;6;5), А2 (6;9;4), А3 (2;10;10), А4 (7;5;9).
-
А1 (3;5;4), А2 (8;7;4), А3 (5;10;4), А4 (4;7;8).
-
А1 (10;6;6), А2 (-2;8;2), А3 (6;8;9), А4 (7;10;3).
-
А1 (1;8;2), А2 (5;2;6), А3 (5;7;4), А4 (4;10;9).
-
А1 (6;6;5), А2 (4;9;5), А3 (4;6;11), А4 (6;9;3).
-
А1 (7;2;2), А2 (5;7;7), А3 (5;3;1), А4 (2;3;7).
-
А1 (8;6;4), А2 (10;5;5), А3 (5;6;8), А4 (8;10;7).
-
А1 (7;7;3), А2 (6;5;8), А3 (3;5;8), А4 (8;4;1).
-
Уравнение одной из сторон квадрата х + 3у – 5 = 0. Составить уравнения трех остальных сторон квадрата, если (-1;0) – точка пересечения его диагоналей.
-
Даны уравнения одной из сторон ромба х - 3у + 10 = 0 и одной из его диагоналей х + 4у – 4 = 0; диагонали ромба пересекаются в точке (0, 1). Найти уравнения остальных сторон ромба.
-
Уравнения двух сторон параллелограмма х + 2у + 2 = 0 и х + у = 0, а уравнение одной из его диагоналей х – 2 = 0. Найти координаты вершин параллелограмма.
-
Даны две вершины А(-3;3) и В(5;-1) и точка D(4;3) пересечения высот треугольника. Составить уравнения его сторон.
-
Даны вершины А(-3;-2), В(4;-1), С(1;3) трапеции АВСD (AD
 ВС).
Известно, что диагонали трапеции взаимно
перпендикулярны. Найти координаты
вершины D
этой трапеции.
ВС).
Известно, что диагонали трапеции взаимно
перпендикулярны. Найти координаты
вершины D
этой трапеции.
-
Даны уравнения двух сторон треугольника 5х - 4у + 15 = 0 и 4х + у – 9 = 0. Его медианы пересекаются в точке (0;2). Составить уравнение третьей стороны треугольника.
-
Даны две вершины А(2;-2) и В(3;-1) и точка Р(1;0) пересечения медиан треугольника АВС. Составить уравнение высоты треугольника, проведенной через третью вершину С.
-
Даны уравнения двух высот треугольника х + у = 4 и у = 2х и одна из его вершин А(0;2). Составить уравнения сторон треугольника.
-
Даны уравнения двух медиан треугольника х - 2у + 1 = 0 и у – 1 = 0 и одна из его вершин (1;3). Составить уравнения его сторон.
-
Две стороны треугольника заданы уравнениями 5х - 2у – 8 = 0 и 3х - 2у – 8 = 0, а середина третьей стороны совпадает с началом координат. Составить уравнение этой стороны.
-
Составить уравнение линии, расстояние каждой точки которой от начала координат и от точки А(5;0) относятся как 2:1.
-
Составить уравнение линии, расстояние каждой точки которой от точки А(-1;0) вдвое меньше расстояния ее от прямой х = - 4.
-
Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 5х + 8 = 0 относятся как 5 : 4.
-
Составить уравнение линии, каждая точка которой находится вдвое дальше от точки А(4;0), чем от точки В(1;0).
-
Составить уравнение линии, расстояния каждой точки которой от точки А(2;0) и от прямой 2х + 5 = 0 относятся как 4 : 5.
-
Составить уравнение линии, расстояние каждой точки которой от точки А(3;0) вдвое меньше расстояния от точки В(26;0).
-
Составить уравнение линии, каждая точка которой одинаково удалена от точки А(0;2) и от прямой у – 4 = 0.
-
Составить уравнение линии, каждая точка которой равноотстоит от оси ординат и от окружности х2 + у2 = 4х.
-
Составить уравнение линии, каждая точка которой равноудалена от точки А(2;6) и о прямой у + 2 = 0.
-
Составить уравнение линии, каждая точка которой отстоит от точки А(-4;0) втрое дальше, чем от начала координат.
-
– 50. Линия задана уравнением r = r(φ) в полярной системе координат. Требуется: 1) построить линию по точкам, начиная от φ = 0 до φ = 2π и придавая φ значения через промежуток π/8; 2) найти уравнение данной линии в прямоугольной декартовой ситеме координат, у которой начало координат совпадает с полюсом, а положительная полуось абсцисс – с полярной осью; 3) по полученному уравнению определить, какая это линия.
41.
![]()
43.
![]()
45.
![]()
47.
![]()
49.
![]()
42.
![]()
44.
![]()
46.
![]()
48.
![]()
50.
![]()
51 - 60. Дана система линейных уравнений:

Доказать ее совместность и решить двумя способами: 1) методом Гаусса; 2) средствами матричного исчисления.
51.
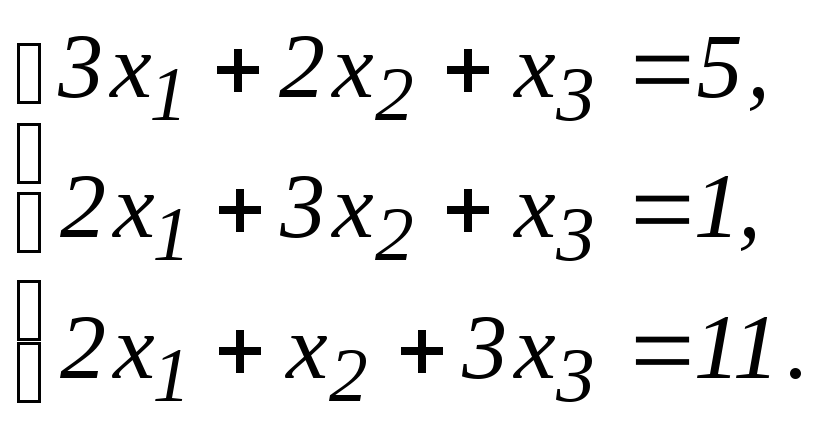 52.
52.

53.
 54.
54.

55.
 56.
56.

57.
 58.
58.

59.
 60.
60.

61 - 80. Решить систему трех уравнений с тремя неизвестными при помощи определителей.
61.
 62.
62.

63.
 64.
64.

65.
 66.
66.

67.
 68.
68.

69.
 70.
70.

71.
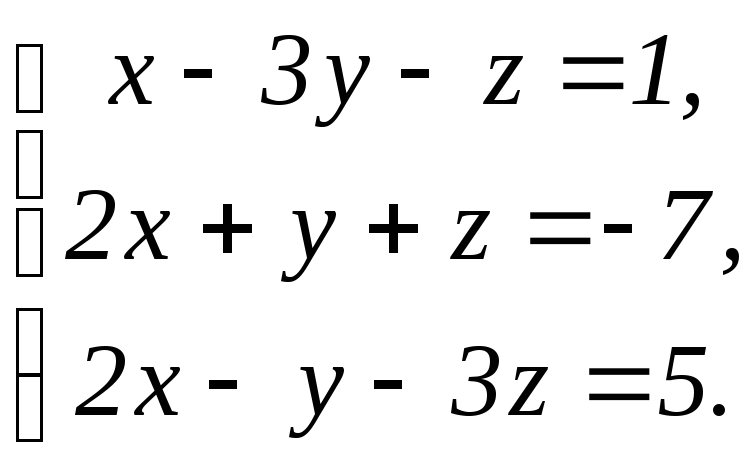 72.
72.

73.
 74.
74.
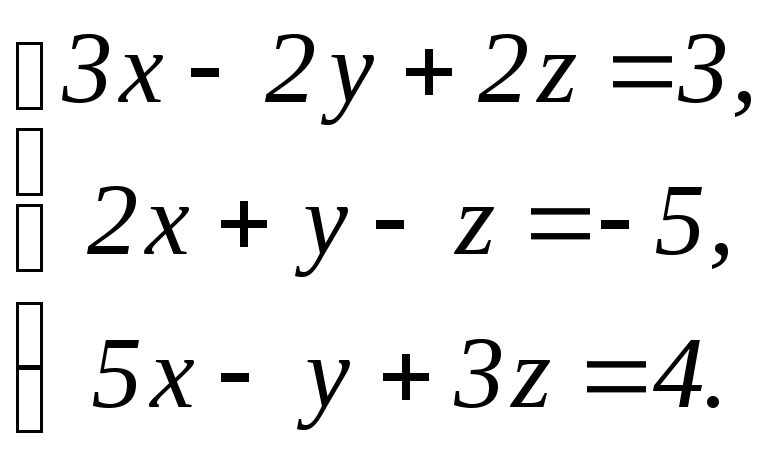
75.
 76.
76.

77.
 78.
78.

79.
 80.
80.

Контрольная работа №2
81 - 90. Дано комплексное число а. Требуется:1) записать число а в алгебраической и тригонометрической формах; 2) найти все корни уравнения z3 + а = 0.
81.
![]() .
82.
.
82.
![]() .
.
83.
![]() .
84.
.
84.
![]()
85.
![]() .
86.
.
86.
![]()
87.
![]() .
88.
.
88.
![]() .
.
89.
![]() .
90.
.
90.
![]() .
.
91 - 95. Построить график функции у = Аsin(ax+b) преобразованием графика функции у = sin x.
91.
![]() .
.
92.
![]() .
.
93.
![]() .
.
94.
![]() .
.
95.
![]() .
.
96 - 100. Построить график функции y = A cos(ax+b) преобразованием графика функции y = cos x.
96.
![]() .
.
97.
![]() .
.
98.
![]() .
.
99.
![]() .
.
100.
![]() .
.
101 - 120. Найти пределы функций, не пользуясь правилом Лопиталя.
|
101. |
а)
|
б)
|
|
в)
|
г)
|
|
|
102. |
а)
|
б)
|
|
в)
|
г)
|
|
|
103. |
а)
|
б)
|
|
в)
|
г)
|
|
|
104. |
а)
|
б)
|
|
в)
|
г)
|
|
|
105. |
а)
|
б)
|
|
в)
|
г)
|
|
|
106. |
а)
|
б)
|
|
в)
|
г)
|
|
|
107. |
а)
|
б)
|
|
в)
|
г)
|
|
|
108. |
а)
|
б)
|
|
в)
|
г)
|
|
|
109. |
а)
|
б)
|
|
в)
|
г)
|
|
|
110. |
а)
|
б)
|
|
в)
|
г)
|
|
|
111. |
а)
|
б)
|
|
в)
|
г)
|
|
|
112. |
а)
|
б)
|
|
в)
|
г)
|
|
|
113. |
а)
|
б)
|
|
в)
|
г)
|
|
|
114. |
а)
|
б)
|
|
в)
|
г)
|
|
|
115. |
а)
|
б)
|
|
в)
|
г)
|
|
|
116. |
а)
|
б)
|
|
в)
|
г)
|
|
|
117. |
а)
|
б)
|
|
в)
|
г)
|
|
|
118. |
а)
|
б)
|
|
в)
|
г)
|
|
|
119. |
а)
|
б)
|
|
в)
|
г)
|
|
|
120. |
а)
|
б)
|
|
в)
|
г)
|
121 - 130. Задана функция y = f(x) и два значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной для каждого из данных значений аргумента; 2) в случае разрыва функции найти ее пределы в точке разрыва слева и справа; 3) сделать схематический чертеж.
121. f(x)=91/(2-x), x1=0, x2=2.
123. f(x)=121/x, x1=0, x2=2.
125. f(x)=81/(5-x), x1=3, x2=5.
127. f(x)=141/(6-x), x1=4, x2=6.
129. f(x)=111/(4+x), x1=-4, x2=-2.
122. f(x)=41/(3-x), x1=1, x2=3.
124. f(x)=31/(4-x), x1=2, x2=4.
126. f(x)=101/(7-x), x1=5, x2=7.
128. f(x)=151/(8-x), x1=6, x2=8.
130. f(x)=131/(5+x), x1=-5, x2=-3.
В задачах 131 - 140 даны функции y = f(x) и значения аргумента х1 и х2. Требуется: 1) установить, является ли данная функция непрерывной или разрывной при данных значениях аргумента; 2) найти односторонние пределы в точках разрыва; 3)построить график данной функции.
131.
![]()
133.
![]()
135.
![]()
137.
![]()
139.
![]()
132.
![]()
134
![]()
136.
![]()
138.
![]()
140.
![]()
В задачах 141 - 150 функция у задана различными аналитическими выражениями для различных областей изменения аргумента х. Требуется: 1) найти точки разрыва функции, если они существуют; 2) найти односторонние пределы и скачок функции в точках разрыва; 3) сделать чертеж.
|
141. |
|
146. |
|
|
142. |
|
147. |
|
|
143. |
|
148. |
|
|
144. |
|
149. |
|
|
145. |
|
150. |
|
151 - 160. Задана функция y = f(x). Найти точки разрыва функции, если они существуют. Сделать чертеж.
151.


152.


153.

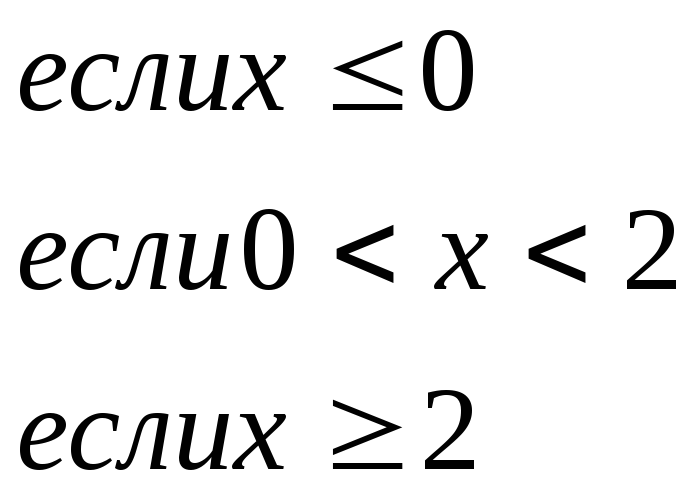
154.

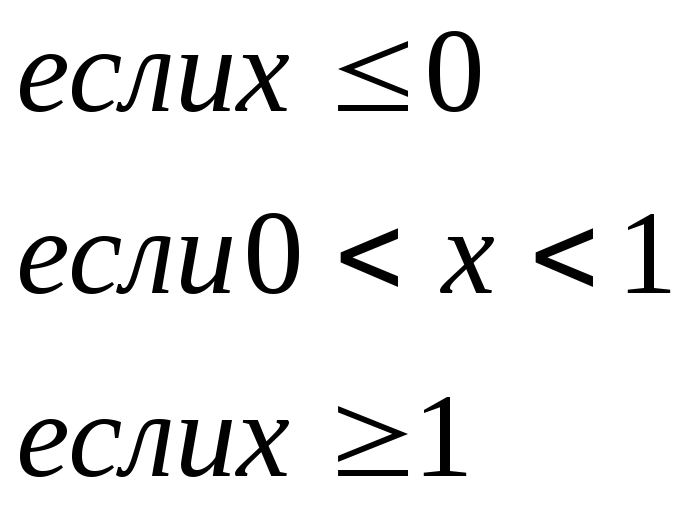
155.


156.


157.


158.


159.


160.


Контрольная работа №3
161
- 170. Найти
производные
![]() данных функций.
данных функций.
|
161. |
|
162. |
|
|
163. |
|
164. |
|
|
165. |
|
166. |
|
|
167. |
|
168. |
|
|
169. |
|
170. |
|
171
- 180. Найти
![]() и
и
![]()
171.
![]()
![]()
![]()
172.
![]()
![]()
![]()
173.
![]()
![]()
![]()
174.
![]()
![]()
![]()
175.
![]()
![]()
![]()
176.
![]()
![]()
![]()
177.
![]()
![]()
![]()
178.
![]()
![]() ,
,
![]()
179.
![]()
![]()
![]()
180.
![]()
![]()
![]() .
.
181
- 190. Найти
наибольшее и наименьшее значения
функции у =
f(x)
на отрезке
![]()
181.
![]()
182.
![]()
183.
![]()
184.
![]()
185.
![]()
186.
![]()
187.
![]()
188.
![]()
189.
![]()
190.
![]()
191 - 210. Исследовать методами дифференциального исчисления функцию и, используя результаты исследования, построить ее график.
191. у = 4х/(4+х2) 192. y = (x2-1)/(x2 +1)
193. y = (x2+1)/(x2-1) 194. y = x2/(x-1)
195. y = x3/(x2+1) 196. y = (4x3+5)/x
197. y = (x2-5)/(x-3) 198. y = x4/(x3-1)
199. y = 4x3/(x3-1) 200. y = (2-4x2)/(1-4x2)
201.
y
=
(1nx)/![]() 202.
y
=
x
202.
y
=
x![]()
203.
y
=
![]() 204.
y
=
x2-21nx
204.
y
=
x2-21nx
205. y = 1n (x2-4) 206. y = e1/(2-x)
207.
y
=
1n
(x2+1)
208.
y
=
(2+x2)![]()
209. y = 1n (9-x2) 210. y = (x-1)e3x+1.
211.
Дана функция z
= y/(x2-
y2)5.
Показать, что
![]()
212.
Дана функция z
= y2/(3x)+arcsin(xy).
Показать, что
![]()
213.
Дана функция z
= 1n(x2+y2+2x+1).
Показать, что
![]()
214.
Дана функция z
= exy.
Показать, что
![]()
215.
Дана функция z
= 1n(x+e-y).
Показать, что
![]()
216.
Дана функция z
= x/y.
Показать, что
![]()
217.
Дана функция z
= xy.
Показать, что
![]()
218.
Дана функция z
= xey/x.
Показать, что
![]()
219.
Дана функция z
= sin(x+ay).
Показать, что
![]()
220.
Дана функция z
= cosy+(y
- x)siny.
Показать, что
![]()
221
- 230. Дана
функция z
= f(x,y)
и две точки А(х0,
у0)
и В(х1,
у1).
Требуется: вычислить значение z1
функции в точке В;
2) вычислить приближенное значение
![]() функции в точке В,
исходя из значения z0
функции в точке А,
заменив приращение функции при переходе
от точки А
к точке В
дифференциалом, и оценить в процентах
относительную погрешность, возникающую
при замене приращения функции ее
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
z
= f(x,y)
в точке С(х0,
у0,
z0).
функции в точке В,
исходя из значения z0
функции в точке А,
заменив приращение функции при переходе
от точки А
к точке В
дифференциалом, и оценить в процентах
относительную погрешность, возникающую
при замене приращения функции ее
дифференциалом; 3) составить уравнение
касательной плоскости к поверхности
z
= f(x,y)
в точке С(х0,
у0,
z0).
221. z = x2+xy+y2; А(1;2), В(1,02;96)
222. z = 3x2-xy+x+y; А(1;3), В(1,06;2,92)
223. z = x2+3xy-6y; А(4;1), В(3,96;1,03)
224. z = x2-y2+6x+3y; А(2;3), В(2,02;2,97)
225. z = x2+2xy+3y2 ; А(2;1), В(1,96;1,04)
226. z = x2+y2+2x+y-1; А(2;4), В(1,98;3,91)
227. z = 3x2+2y2-xy; А(-1;3), В(-0,98;2,97)
228. z = x2-y2+5x+4y; А(3;3), В(3,02;2,98)
229. z = 2xy+3y2-5x; А(3;4), В(3,04;3,95)
230. z = xy+2y2-2x; А(1;2), В(0,97;2,03).
231 - 240. Найти наименьшее и наибольшее значения функции z = f(x,y) в замкнутой области D, заданной системой неравенств. Сделать чертеж.
231.
z
= x2+y2-9xy+27;
![]()
![]() .
.
232.
z
= x2+2y2+1;
![]()
![]() .
.
233.
z
= 3-2x2-xy-y2;
![]()
![]() .
.
234.
z
= x2+3y2+x-y;
![]()
![]()
235.
z
= x2+2xy+2y2;
![]()
![]() .
.
236.
z
= 5x2-3xy+y2+4;
![]()
![]()
237.
z = 10+2xy-x2;
![]()
238.
z
= x2+2xy-y2+4x;
![]()
![]() .
.
239.
z
= x2+xy-2;
![]()
240.
z
= x2+xy;
![]()
![]() .
.
241 - 250. Даны функции z = z(x,y), точка А(х0,у0) и вектор а. Найти; 1) grad z в точке А; 2)производную в точке А по направлению вектора а.
241. z = x2+xy+y2; А(1;1), а = 2i-j.
242. z = 2x2+3xy+y2; А(2;1), a = 3i-4j.
243. z = 1n(5x2+3y2); А(1;1), a = 3i+2j.
244. z = 1n(5x2+4y2); А(1;1), a = 2i-j.
245. z = 5x2+6xy; А(2;1), a = i+2j.
246. z = arctg(xy2); А(2;3), a = 4i-3j.
247. z = arcsin (x2/y); А(1;2), a = 5i-12j.
248. z = 1n(3x2+4y2); А(1;3), a = 2i-j.
249. z = 3x4+2x2y3; А(-1;2), a = 4i-3j.
250. z = 3x2y2+5y2x; А(1;1), a = 2i+j.
251 - 260. Экспериментально получены пять значений искомой функции y = f(x) при пяти значениях аргумента, которые записаны в таблице. Методом наименьших квадратов найти функцию y = f(x) в виде у = ах + b.
251.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
4,3 |
5,3 |
3,8 |
1,8 |
2,3 |
252.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
4,5 |
5,5 |
4,0 |
2,0 |
2,5 |
253.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
4,7 |
5,7 |
4,2 |
2,2 |
2,7 |
254.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
4,9 |
5,9 |
4,4 |
2,4 |
2,9 |
255.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
5,1 |
6,1 |
4,6 |
2,6 |
3,1 |
256.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
3,9 |
4,9 |
3,4 |
1,4 |
1,9 |
257.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
5,2 |
6,2 |
4,7 |
2,7 |
3,2 |
258.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
5,5 |
6,5 |
5,0 |
3,0 |
3,5 |
259.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
5,7 |
6,7 |
5,2 |
3,2 |
3,7 |
260.
|
х |
1 |
2 |
3 |
4 |
5 |
|
у |
5,9 |
6,9 |
5,4 |
3,4 |
3,9 |
Контрольная работа №4
261 - 270. Найти неопределенные интегралы. В двух первых примерах а) и б) проверить результаты дифференцированием.
261.
![]()
![]()
![]()
![]()
262.
![]()
![]()
![]()
![]()
263.
![]()
![]()
![]()
![]()
264.
![]()
![]() ;
;
![]()
![]()
265.
![]()
![]() ;
;
![]()
![]()
266.
![]()
![]()
![]()

267.
![]()
![]()
![]()
![]()
268.
![]()
![]()
![]()
![]()
269.
![]()
![]()
![]()
![]()
270.
![]()
![]()
![]()
![]()
271
- 280. Вычислить
приближенное значение определенного
интеграла
![]() с помощью формулы Симпсона, разбив
отрезок интегрирования на 10 частей.
Все вычисления производить с округлением
до третьего десятичного знака.
с помощью формулы Симпсона, разбив
отрезок интегрирования на 10 частей.
Все вычисления производить с округлением
до третьего десятичного знака.
271.
![]()
273.
![]()
272.
![]()
274.
![]()
275.
![]()
277.
![]()
279.
![]()
276.
![]()
278.
![]()
280.
![]()
281 - 290. Вычислить несобственный интеграл или доказать его расходимость.
281.
![]()
283.
![]()
285.
![]()
287.
![]()
289.

282.
![]()
284.
![]()
286.
![]()
288.
![]()
290.
![]()
291. Вычислить площадь фигуры, ограниченной параболой у = 3х2 + 1 и прямой у = 3х + 7.
292.
Вычислить площадь фигуры, ограниченной
одной аркой циклоды х
= а(t
- sin
t),
y
= a(1
- cos
t),
![]() и осью Ох.
и осью Ох.
293. Вычислить площадь фигуры, ограниченной кардиоидой r = 3(1 + cos φ).
294. Вычислить площадь фигуры, ограниченной четырехлепестковой розой r = 4sin 2φ.
295.
Вычислить объем тела, образованного
вращением вокруг оси Ох фигуры,
ограниченной параболами у
= х2
и у =![]() .
.
296.
Вычислить объем тела, образованного
вращением вокруг оси Ох фигуры,
ограниченной полуэллипсом у
=
![]() ,
параболой х
=
,
параболой х
=
![]() и осью Оу.
и осью Оу.
297. Вычислить объем тела, образованного вращением вокруг оси Оу фигуры, ограниченной кривыми у = 2/(1 + х2)4 и у = х2.
298.
Вычислить длину дуги полукубической
параболы у
=![]() от
точки А
(2;0) до точки В
(6;8).
от
точки А
(2;0) до точки В
(6;8).
299. Вычислить длину кардиоиды r = 3(1 - cosφ).
300.
Вычислить длину одной арки циклоиды х
= 3(t
- sint),
y
= 3(1 - cost),
![]() .
.
301 - 320. Найти общее решение дифференциального уравнения.
301.
![]()
302.
![]()
303.
![]()
304.
![]()
305.
![]()
306.
![]()
307.
![]()
308.
![]()
309.
![]()
310.
![]()
311.
![]()
312.
![]()
313.
![]()
314.
![]()
315.
![]()
316.
![]()
317.
![]()
318.
![]()
319.
![]()
320.
![]()
В задачах 321 - 330 даны дифференциальные уравнения второго порядка, допускающие понижение порядка. Найти частное решение, удовлетворяющее указанным начальным условиям.
321. у΄΄- еуу΄= 0, у(0) = 0, у΄(0) = 1.
322. у΄у΄΄= 2у, у(0) = 0, у΄(0) = 0.
323. уу΄΄= (у΄)2, у(0) = 1, у΄(0) = 3.
324. у3у΄΄= 3, у(1) = 1, у΄(1) = 1.
325. у΄΄-12у2= 0, у(0) =1/2, у΄(0) = 1.
326. 2у΄΄=е4у, у(0) = 0, у΄(0) = ½.
327. (у – 2)у΄΄ = 2(у΄)2, у(0) = 3, у΄(0) = 1.
328. 2уу΄΄= 3 + (у΄)2, у(1) = 1, у΄(1) = 1.
329.
у΄΄=
![]() у(2) = 0, у΄(2) = 2.
у(2) = 0, у΄(2) = 2.
330. (у + 1)2у΄΄= (у΄)3, у΄(0) = 1.
331
- 340. Найти
частное решение дифференциального
уравнения
![]() ,
удовлетворяющее начальным условиям
у(0)=у0,
,
удовлетворяющее начальным условиям
у(0)=у0,
![]()
331.
![]()
![]()
332.
![]()
![]()
333.
![]()
![]()
334.
![]()
![]()
335.
![]()
![]()
336.
![]()
![]()
337.
![]()
![]()
338.
![]()
![]()
339.
![]()
![]()
340.
![]()
![]()
В задачах 441 - 450 даны линейные неоднородные дифференциальные уравнения второго полрядка с постоянными коэффициентами. Найти частное решение, удовлетворяющее указанным начальным условиям.
441. y΄΄-2y΄-8y=16x2+2, y(0)=0, y΄(0)=5.
442. y΄΄+4y=3cos x, y(0)=1, y΄(0)=2.
443. y΄΄-y΄-2y=3e2x, y(0)=2, y΄(0)=5.
444. y΄΄-2y΄=2x+1, y(0)=1, y΄(0)=1.
445. y΄΄-2y΄+y=9e-2x+2x-4, y(0)=1, y΄(0)=1.
446. y΄΄-4y=4sin 2x, y(0)=2, y΄(0)=7.
447. y΄΄+y΄=3cos x – sin x, y(0)=0, y΄(0)=1.
448. y΄΄-y΄-6y=6x2-4x-3, y(0)=3, y΄(0)=5.
449. y΄΄-3y΄=3e3x, y(0)=2, y΄(0)=4.
450. y΄΄-4y΄+5y=5x – 4, y(0)=0, y΄(0)=3.
351 - 360. Дана система линейных дифференциальных уравнений с постоянными коэффициентами

Требуется найти общее решение системы.
351.

353.

355.

357.

359.

352.

354.

356.

358.

360.

Контрольная работа №5
361.
Вычислить площадь фигуры, ограниченной
параболами
![]() и
и
![]() .
.
362. Вычислить площадь фигуры, ограниченной эллипсом x = acos t, y = bsint.
363. Вычислить площадь фигуры, ограниченной астроидой x = 4cos3t, y = 4sin3t.
364.
Найти объем тела, образованного вращением
вокруг оси Ох фигуры, ограниченной
параболой
![]() ,
х = 4
и осью Ох.
,
х = 4
и осью Ох.
365. Найти объем тела, полученного вращением вокруг оси Оу фигуры, ограниченной гиперболой у = 6/х, осью Оу и прямыми у = 1 и у = 6.
366. Найти объем тела, полученного вращением вокруг оси Ох эллипса х = аcost, y = bsint.
367.
Найти длину дуги кривой
![]() от х1
= 0 до
х2
= 12.
от х1
= 0 до
х2
= 12.
368. Найти длину дуги кривой у = lnx от х1= ¾ до х2 = 2,4.
369. Найти длину одной арки циклоиды х = а(t - sint), y = a(1-cost).
370. Найти длину кардиоиды r = 2a(1-cosφ).
В задачах 371 - 380 вычислить объем тела, ограниченного указанными поверхностями. Данное тело и область интегрирования изобразить на чертеже.
371.
![]()
372.
![]()
373.
![]()
374.
![]()
375.
![]()
376.
![]()
377.
![]()
378.
![]()
379.
![]()
380.
![]()
381 - 390. Вычислить с помощью тройного интеграла объем тела, ограниченного указанными поверхностями. Сделать чертежи данного тела и его проекции на плоскость хОу.
381.
z = 0, z
= x,
у = 0, y
= 4, x
=
![]() .
.
382. z = 0, z = 9 - y2, x2 + y2 = 9.
383. z = 0, z = 4 – x - y, x2 + y2 = 4.
384. z = 0, z = y2, x2 + y2 = 9.
385. z = 0, y + z = 2, x2 + y2 = 4.
386. z = 0, 4z = y2, 2x – y = 0, x + y = 9.
387. z = 0, x2 + y2 = z, x2 + y2 = 4.
388. z = 0, z = 1 - y2, x = y2, x = 2y2 + 1.
389. z = 0, z = 1 - x2, y = 0, y = 3 - x.
390.
z
= 0, z
= 4![]() ,
x
= 0, x
+ y
= 4.
,
x
= 0, x
+ y
= 4.
391. Вычислить криволинейный интеграл
![]()
вдоль дуги L окружности х = 5cos t, y =5sin t, обходя ее против хода часовой стрелки от точки А(5;0) до точки В(0;5). Сделать чертеж.
392. Вычислить криволинейный интеграл
![]()
вдоль ломаной L = OAB, где О(0;0), А(2;0), В(4;5). Сделать чертеж.
393. Вычислить криволинейный интеграл
![]()
вдоль границы L треугольника АВС, обходя ее против хода часовой стрелки, если А(1;0), В(1;1), С(0;1). Сделать чертеж.
394. Вычислить криволинейный интеграл
![]()
вдоль дуги L параболы у = х2 от точки А(-1;1) до точки В(1;1). Сделать чертеж.
395. Вычислить криволинейный интеграл
![]()
вдоль
верхней половины L
эллипса х =
3cos
t,
y
= 2sin
t
![]() .
Сделать чертеж.
.
Сделать чертеж.
396. Вычислить криволинейный интеграл
![]()
вдоль ломаной L = ABC, где А(1;2), В(1;5), С(3;5). Сделать чертеж.
397. Вычислить криволинейный интеграл
![]()
вдоль дуги L кривой у = е-х от точки А(0;1) до точки В(-1;е). Сделать чертеж.
398. Вычислить криволинейный интеграл
![]()
вдоль отрезка L = AB прямой от точки А(1;2) до точки В(2;4). Сделать чертеж.
399. Вычислить криволинейный интеграл
![]()
вдоль дуги L параболы у = 2х2 от точки А(0;0) до точки В(1;2). Сделать чертеж.
400. Вычислить криволинейный интеграл
![]()
вдоль дуги L кривой у =1n x от точки А(1;0) до точки В(е;1). Сделать чертеж.
В задачах 401 - 410 найти функцию U(x, y) по ее полному дифференциалу dU.
401.
![]()
402.
![]()
403.
![]()
404.
![]()
405.
![]()
406.
![]()
407.
![]()
408.
![]()
409.
![]()
410.
![]()
411 - 420. Исследовать сходимость числового ряда.
411.
![]()
412.
![]()
413.
![]()
415.
![]()
417.
![]()
419.
![]()
414.
![]()
416.
![]()
418.
![]()
420.
![]()
421 - 430. Найти интервал сходимости степенного ряда.
421.
![]() 422.
422.
![]()
423.
![]() 424.
424.
![]()
425.
![]() 426.
426.
![]()
427.
![]() 428.
428.
![]()
429.
![]() 430.
430.
![]()
431
- 440. Вычислить
определенный интеграл
![]() с точностью до 0,001, разложив подынтегральную
функцию в ряд и затем проинтегрировав
его почленно.
с точностью до 0,001, разложив подынтегральную
функцию в ряд и затем проинтегрировав
его почленно.
431.
![]()
433.
![]()
432.
![]()
434.
![]()
435.
![]()
437.
![]()
439.
![]()
436.
![]()
438.
![]()
440.
![]()
Контрольная работа №6
441
- 450. Методом
Даламбера найти уравнение и
= и(х, t)
формы однородной бесконечной струны,
определяемой волновым уравнением
![]() ,
если в начальный момент tо
= 0
форма струны и скорость точки струны
с абсциссой х определяются соответственно
заданными функциям
,
если в начальный момент tо
= 0
форма струны и скорость точки струны
с абсциссой х определяются соответственно
заданными функциям
![]()
441. f(x)=x(2-x), F(x)=e-x.
442. f(x)=x2, F(x)= sin x.
443. f(x)=ex, F(x)=ωx.
444. f(x)=cos x, F(x)=ωx.
445. f(x)=sin x, F(x)=υ0.
446. f(x)=x, F(x)= cos x.
447. f(x)= sin x, F(x)= cos x.
448. f(x)=x(x-2), F(x)= ex .
449. f(x)= cos x, F(x)= υ0.
450. f(x)=e-x, F(x)= sin x.
451-460. Методом Фурье
найти решение
![]()
![]() уравнения теплопроводности
уравнения теплопроводности![]() ,
если в начальный момент времени
,
если в начальный момент времени
![]() температура стержня длины
температура стержня длины
![]() определяется заданной функцией
определяется заданной функцией
![]() ,
а на границах стержня температура
задается постоянной и равной, т.е.
,
а на границах стержня температура
задается постоянной и равной, т.е.
![]() .
.
451. f(x)=x
452. f(x)=1
453. f(x)=x-1
454. f(x)=x+1
455. f(x)=2x-1
456. f(x)=2x+1
457. f(x)=1-3x
458. f(x)=![]()
459.
f(x)=![]()
460. f(x)=1-2x
461 - 470. Методом операционного исчисления найти частное решение дифференциального уравнения, удовлетворяющее заданным начальным условиям.
461.
![]() ,
,
![]()
462.
![]() ,
,
![]()
463.
![]() ,
,
![]()
464.
![]() ,
,
![]()
465.
![]() ,
,
![]()
466.
![]() ,
,
![]()
467.
![]() ,
,
![]()
468.
![]() ,
,
![]()
469.
![]() ,
,
![]()
470.
![]() ,
,
![]()
471 - 480. Методом операционного исчисления найти частное решение системы дифференциальных уравнений, удовлетворяющее начальным условиям.
471.
 x(0)=1,
y(0)=0.
x(0)=1,
y(0)=0.
472.
 x(0)=1,
y(0)=1, z(0)=1.
x(0)=1,
y(0)=1, z(0)=1.
473.
 x(0)=2,
y(0)=3.
x(0)=2,
y(0)=3.
474.
 x(0)=2, y(0)=1/2, z(0)=5/2.
x(0)=2, y(0)=1/2, z(0)=5/2.
475.
 x(0)=1, y(0)=1.
x(0)=1, y(0)=1.
476.
 x(0)=2, y(0)=2, z(0)=-1.
x(0)=2, y(0)=2, z(0)=-1.
477.
 x(0)=0, y(0)=0.
x(0)=0, y(0)=0.
478.
 x(0)=1,
y(0)=2, z(0)=3.
x(0)=1,
y(0)=2, z(0)=3.
479.
 x(0)=1,
y(0)=-1.
x(0)=1,
y(0)=-1.
480.
 x(0)=1,
y(0)=1.
x(0)=1,
y(0)=1.
481. Студент знает 45 из 60 вопросов программы. Каждый экзаменационный билет содержит три вопроса. Найти вероятность того, что: а) студент знает все три вопроса; б) только два вопроса; в) только один вопрос экзаменационного билета.
482. В каждой из двух урн находятся 5 белых и 10 черных шаров. Из первой урны во вторую переложили неудачу один шар, а затем из второй урны вынули наугад один шар. Найти вероятность того, что вынутый шар окажется черным.
483. Три стрелка в одинаковых и независимых условиях производили по одному выстрелу по одной и той же целию Вероятность поражения цели первым стрелком равна 0,9, вторым – 0,8, третьим – 0,7. Найти вероятность того, что: а) только один из стрелков попадает в цель; б) только два стрелка попадут в цель; в) все три стрелка попадут в цель.
484. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 1600 испытаниях событие наступит 1200 раз.
485. Для сигнализации об аварии установлены три независимо работающих устройства. Вероятность того, что при аварии сработает первое устройство, равна 0,9, второе – 0,95, третье – 0,85. Найти вероятность того, что при аварии сработает: а) только одно устойство; б) только два устройства; в) все три устройства.
486. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,02. Найти вероятность того, что в 150 испытаниях событие наступит 5 раз.
487. В партии из 1000 изделий имеются 10 дефектных. Найти вероятность того, что среди 50 изделий, наудачу взятых из этой партии, ровно три окажутся дефектными.
488. Вероятность наступления события в каждом из одинаковых и независимых испытаний равна 0,8. Найти вероятность того, что в 125 испытаниях событие наступит не менее 75 и не более 90 раз.
489. На трех станках при одинаковых и независимых условиях изготовляют детали одного наименования. На первом станке изготовляют 10%, на втором – 30, на третьем – 60% всех деталей. Вероятность каждой детали быть бездефектной равна 0,7, если она изготовлена на первом станке, 0,8, - если на втором станке, и 0,9, - если на третьем станке. Найти вероятность того, что наугад взятая деталь окажется бездефектной.
490. Два брата входят в состав двух спортивных команд, состоящих из 12 человек каждая. В двух урнах имеются по 12 билетов с номерами от 1до 12. Члены каждой команды вынимают наудачу по одному билету из определенной урны (без возвращения). Найти вероятность того, что оба брата вытащат билет номер 6.
491 - 500. Задан закон распределения случайной величины X – размер деталей, выпускаемых заводом ( в первой строке таблицы даны возможные значения измеренной детали, а во второй строке указаны вероятности p этих возможных значений).
Найти: 1)
математическое ожидание M(X);
2) дисперсию D(X);
3) среднее квадратическое отклонение
![]() .
.
|
491. |
X |
23 |
25 |
28 |
29 |
|
P |
0.3 |
0.2 |
0.4 |
0.1 |
|
|
|
|
|
|
|
|
|
492. |
X |
17 |
21 |
25 |
27 |
|
P |
0.2 |
0.4 |
0.3 |
0.1 |
|
|
|
|
|
|
|
|
|
493. |
X |
24 |
26 |
28 |
30 |
|
P |
0.2 |
0.2 |
0.5 |
0.1 |
|
|
|
|
|
|
|
|
|
494. |
X |
12 |
16 |
19 |
21 |
|
P |
0.1 |
0.5 |
0.3 |
0.1 |
|
|
|
|
|
|
|
|
|
495. |
X |
25 |
27 |
30 |
32 |
|
P |
0.2 |
0.4 |
0.3 |
0.1 |
|
|
|
|
|
|
|
|
|
496. |
X |
30 |
32 |
35 |
40 |
|
P |
0.1 |
0.5 |
0.2 |
0.2 |
|
|
|
|
|
|
|
|
|
497. |
X |
12 |
14 |
16 |
20 |
|
P |
0.1 |
0.2 |
0.5 |
0.2 |
|
|
|
|
|
|
|
|
|
498. |
X |
21 |
25 |
28 |
31 |
|
P |
0.1 |
0.4 |
0.2 |
0.3 |
|
|
|
|
|
|
|
|
|
499. |
X |
60 |
64 |
67 |
70 |
|
P |
0.1 |
0.3 |
0.4 |
0.2 |
|
|
|
|
|
|
|
|
|
500. |
X |
45 |
47 |
50 |
52 |
|
P |
0.2 |
0.4 |
0.3 |
0.1 |
|
|
|
|
|
|
|
|
|
501. |
X |
46 |
49 |
51 |
55 |
|
|
P |
0,2 |
0,3 |
0,1 |
0,4
|
|
502. |
X |
18 |
22 |
23 |
26 |
|
|
P |
0,2 |
0,3 |
0,4 |
0,1
|
|
503. |
X |
78 |
80 |
84 |
85 |
|
|
P |
0,2 |
0,3 |
0,1 |
0,4 |
|
|
|
|
|
|
|
|
504. |
X |
37 |
41 |
43 |
45 |
|
|
P |
0,2 |
0,1 |
0,5 |
0,2 |
|
|
|
|
|
|
|
|
505. |
X |
25 |
28 |
30 |
33 |
|
|
P |
0,1 |
0,2 |
0,4 |
0,3 |
|
|
|
|
|
|
|
|
506. |
X |
56 |
58 |
60 |
64 |
|
|
P |
0,2 |
0,3 |
0,4 |
0,1 |
|
|
|
|
|
|
|
|
507. |
X |
31 |
34 |
37 |
40 |
|
|
P |
0,3 |
0,5 |
0,1 |
0,1 |
|
|
|
|
|
|
|
|
508. |
X |
17 |
20 |
23 |
27 |
|
|
P |
0,1 |
0,4 |
0,3 |
0,2 |
|
|
|
|
|
|
|
|
509. |
X |
28 |
32 |
34 |
36 |
|
|
P |
0,1 |
0,2 |
0,2 |
0,5 |
|
|
|
|
|
|
|
|
510. |
X |
35 |
39 |
42 |
46 |
|
|
P |
0,1 |
0,3 |
0,2 |
0,4 |
|
|
|
|
|
|
|
511
- 520. Найти
доверительный интеграл для оценки
математического ожидания а
нормального распределения с надежностью
0,95 зная выборочную среднюю
![]() ,
объем выборки n
и среднее квадратическое отклонение
σ.
,
объем выборки n
и среднее квадратическое отклонение
σ.
511.
![]()
![]()
![]()
512.
![]()
![]()
![]()
513.
![]()
![]()
![]()
514.
![]()
![]()
![]()
515.
![]()
![]()
![]()
516.
![]()
![]()
![]()
517.
![]()
![]()
![]()
518.
![]()
![]()
![]()
519.
![]()
![]()
![]()
520.
![]()
![]()
![]()