Элементы операционного исчисления

Пусть функция f(x) обладает следующими свойствами:

1⁰. f(x) ≡0 при t < 0.

2⁰. |f(x)| < Ме^Sot при t > 0 , где М > 0 и S₀ – некоторые действительные постоянные.

3⁰. На любом конечном отрезке [а, в] положительной полуоси Ot функция f(x) удовлетворяет условием Дирихле, т.е.:

а) ограниченна;

б) либо непрерывна, либо имеет лишь конечное число точек разрыва I рода;

в) имеет конечное число экстремумов.

Такие функции в операционном исчислении называются изображаемыми по Лапласу, или оригиналами.

Пусть р = α + βi - комплексный параметр.

При сформированных условиях интегралсходится и является функцией от р.

Этот интеграл называется интегралом Лапласа, а определяемая им функция комплексного аргумента р называется преобразованием Лапласа от функции f(t) или лапласовым изображением f(t) или просто изображением f(t) .

Таблица изображений основных элементарных функций

№	f (t) при t > 0		№	f (t) при t > 0
1	1		7	eαtcos βt
2			8	eαtsin βt
3	еαt		9
4	at		10	t cos βt
5	cos βt		11	t sin βt
6	sin βt

Тот факт, что функция является изображением оригинала f(t), обозначается следовательно символом f(t).

Если дано линейное дифференцированное уравнение n-го порядка с постоянными коэффициентами

y⁽ⁿ⁾ + a₁y^(n-1) +…+ a_ny = f(t),

правая часть которого f(t) является оригиналом, то и решение этого уравнения, удовлетворяющее произвольным начальным условиям вида:

y (0) = y₀, у΄(0) = y΄₀ , y΄΄=y₀΄΄, … ,y^(n-1)(0) = y^(n-1)₀

(т.е. решение задачи Коши, поставленной для этого уравнения, с начальными условиями при t = 0, служит оригиналом. Обозначая изображение этого решения через , находим изображение левой части исходного дифференцированного уравнения и, приравнивая его к изображению функции f(t) ,приходим к так называемому изображающему уравнению, которое всегда является линейным алгебраическим уравнением относительно . Определив из этого уравнения , находим оригинал у(t).

Пусть оригинал f(t) дифференцируем n раз и его производные до n-го порядка в свою очередь являются оригиналами. Тогда справедлива теорема дифференцирования оригинала:

если f(t), то

f^(k)(t) p^k _-{p^k-1_{· f(0) +p}^k-2_{· f΄(0) + … + f}^k-1_(0)} , (k 1, 2, … , n).

_{В частности :}

_f΄ p · - f(0),

f΄΄(t) p² · - p f(0) - f΄(0),

f΄΄΄(t) p³ · - p² f (0) – p f΄ (0) - f΄΄(0).

Пример 1. Решить дифференциальное уравнение

y΄΄΄-6y΄΄+11y΄-6y=0, если у(0) = 0, у΄(0) = 1, у΄΄(0) = 0.

Решение.

Переходя к изображениям по теореме дифференцирования оригинала, получим:

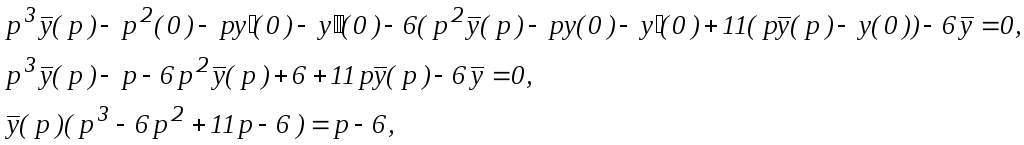
или

Используем элементарные приемы для разложения этой дроби на сумму, таких простейших дробей, оригиналы которых известны:

Полагая р=1, находим –5 = 2А, откуда А = -5/2.

Полагая р=2, находим –4 = -В, откуда В = 4.

При р = 3, находим –3 = 2С, откуда С = -3/2.

Следовательно,

Отсюда, используя формулу (3) таблицы изображений, находим:

Пример 2. Решить систему уравнений: 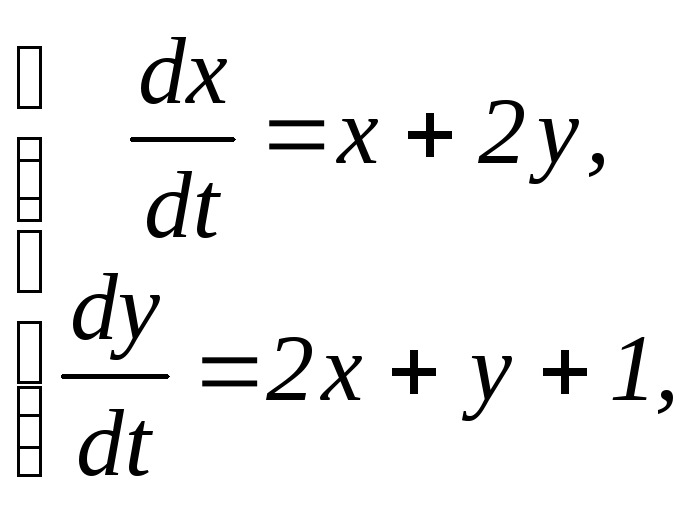если х(0) =0, у (0) = 5.

Решение.

Перейдем к изображениям:

х΄

Система уравнений примет вид:

Из первого уравнения системы выразим , подставим во 2-ое уравнение:

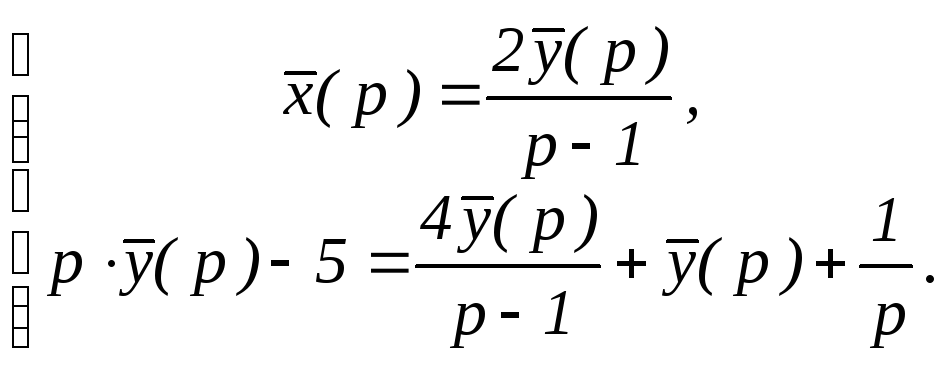
Выразим из 2-го уравнения и подставим в 1-ое:

или

Осталось найти оригинал для и . Разложим дробь на простейшие дроби:

Полагая р =-1 получаем –8 = 4В, откуда В= -2.

Полагая р = 0, получаем 2 = -3А, откуда А =-

Полагая р = 3, получаем 32 = 12 С, откуда С =

Следовательно:

.

Тогда

Аналогично поступим с дробью для отыскивания оригинала для .

При р = -1, 8 = 4В, откуда В = 2.

При р = 0, -1 = -3А, откуда А =

При р = 3, получаем 32 = 12 С, откуда С =

Следовательно:

Тогда

Пример 3. Решить дифференциальное уравнение методом операционного исчисления

у΄΄-2у΄-3у = е^3t, если у(0) = 0, у΄(0) = 0.

Решение

Перейдем к изображениям:

y΄΄

y΄

y

е^3t Тогда данное дифференциальное уравнение примет вид:

или, учитывая начальные условия:

откуда

квадратный трехчлен р²- 2р – 3 можно разложить на два множителя, так как его корни р₁= 3, р₂ = -1: р² – 2р – 3 = (р -3)(р+1).

Окончательно имеем: Осталось найти оригинал данной функции. Разложим полученную рациональную дробь на простейшие дроби:

Полагая р = -1, получаем 1 = 16С, т.е. ;

При р = 3, имеем 1 = 4А, т.е.

Сравнивая коэффициенты при р², получим О = В +С, т. е. Следовательно,

откуда, используя таблицу изображений, находим искомый оригинал и решение данного дифференциального уравнения:

или

Пример 4. Решить систему уравнений: если х(0) = у (0) =1.

Решение.

Перейдя к изображениям имеем:

Из 1-го уравнения системы выразим , подставим во 2-ое уравнение системы:

Из 2-го уравнения системы выразим , подставим в 1-ое уравнение:

Таким образом:

Таким образом:

Разложив, полученные дроби на простейшие, по таблице изображений найдем оригинал:

При р = 5 : 12 = 10А, А = 1, 2. При р =5 : 6 = 10С, С = 0,6.

При р = -5 : 2 =-10В, В = -0,2. При р = -5 : -4 = -10Д, Д = 0,4.

Следовательно, и

Откуда