Занятие 9. Решение уравнений 3-й и 4-й степени

9.1. Решение уравнений 3-й степени

Рассмотрим уравнение

(разделив, если надо, на ). Заменим

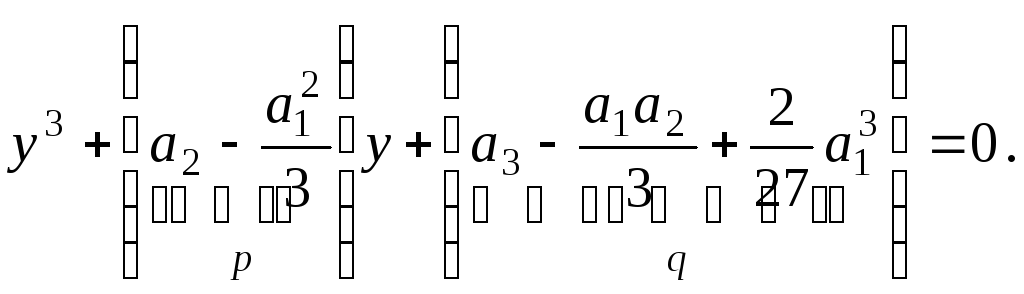
Пусть 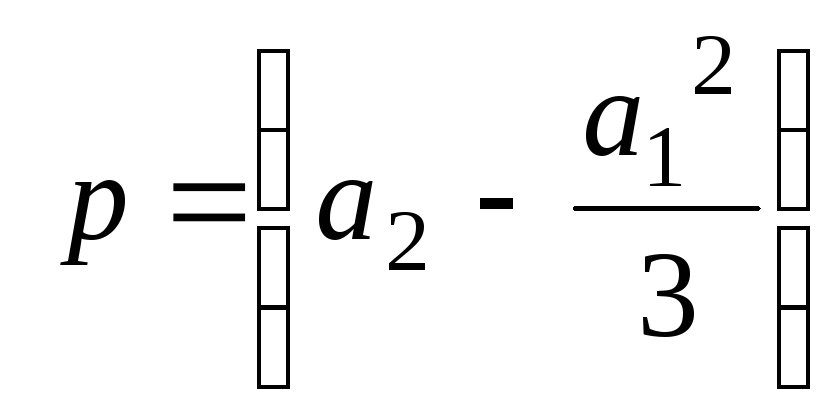и

Обозначим

(9.1)

Положим , где пока неизвестные величины

(9.2)

Пусть удовлетворяют уравнению

(9.3)

Тогда из (9.2)

По теореме Виета неизвестные и удовлетворяют квадратному уравнению:

Решая его, получим

Отсюда

(9.4)

Определение 9.1. Величина называется дискриминантом кубического полинома (9.1)

Формула Кардано

Так как в этой формуле может принимать три значения и тоже три значения, то всевозможных комбинаций может быть девять, а может быть всего три, в силу дополнительной связи (9.3). Если определим из (9.4), то

Тогда

Вспоминая, что

(9.5)

получим

(9.6)

т. е. равно произведению какого-то корня на всё множество кубических корней из 1: где

Соответствующие значения для :

Так как

и

то, подставив полученное значение и в соответствующие значения для , получим:

.

Тогда

где

Пример 9.1. П 75 о).

Таким образом,

Упражнение 9.1. П 75 j), n).

9.2. Решение уравнений 4-й степени

Общий вид уравнения 4-ой степени

Первые два члена можно преобразовать:

Сделаем замену _, тогда

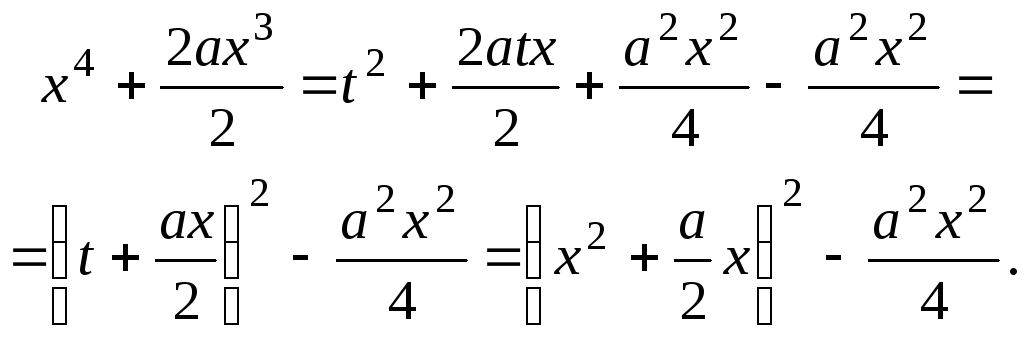
Введем вспомогательную переменную :

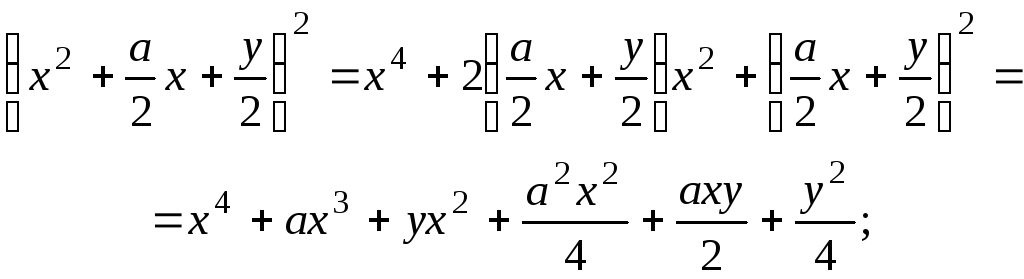
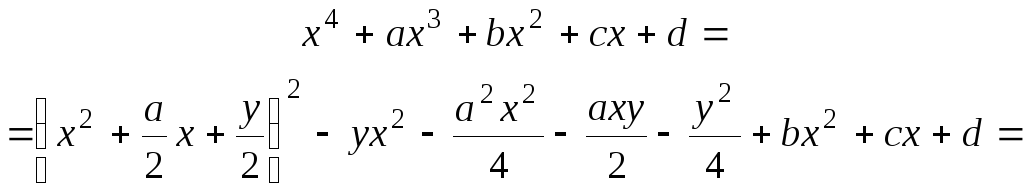
Для того чтобы получить разность квадратов, достаточно воспользоваться введенной переменной так, чтобы получить из второго слагаемого квадрат, а это возможно тогда и только тогда, когда

Пусть - один из корней кубического уравнения. Тогда наше уравнение можно переписать так:

при некоторых и

Приравнивая к нулю каждый из сомножителей, найдем 4етыре корня исходного уравнения.

Уравнение 9.2. П 75j), n); 79 i), j).

Д/з: П 75 (а, b, c), 79 a), 80.

Занятие 12. Полиномы над полем . Приводимость. Полиномы над полем

12.1. Решение уравнений -й степени

Теорема №1

Если f(x) имеет корень равный , такой, что , то f(x) имеет сопряжённый корень.

Упражнение №587(a)

1. (x-1)²*(x-2)*(x-3)*(x-(1+i))*(x-(1-i)) =

= (x²-2x+1)*(x²-5x+6)((x-1)+i)*((x-1)-I )=

= (x⁴-2x²+x²-5x³+10x²-5x+6x²-12x+6)*((x-1)²-i²) =

= (x⁴-7x³+17x²-17x+6)*(x²-2x+1+1) =

= ( x⁴-7x³+17x²-17x+6)*( x²-2x+2) =

= x⁶-7x⁵+17x⁴-17x³+6x²-2x⁵+14x⁴-34x³+34x²-12x+2x⁴-14x³+34x²+12 =

= x⁶-9x⁵+33x⁴-65x³+74x²-46x+12.

Приводимость. Полиномы над полем Q.

Определение №1

f(x) над полем А, отличный от константы, называется непрерывным над полем А, если его нельзя представить в виде произведения двух многочленов меньшей степени с коэффициентов из поля А. Полином, отличный от константы и не являющийся неприводимым называется приводимым. См. Замечание №1 в занятии 9.

Примеры неприводимых полиномов:

1. многочлены первой степени.

2. x²-2 неприводим над полем Q , но приводим над полем R.

3. Ax²+Bx+C или полиномы второй степени. Неприводимы над полем Q.

Границы корней полиномов.

Теорема №2

Пусть f(x)=, . Верхняя граница положительных корней полинома f(x)может быть принята равной одному из чисел.

(Макларен)

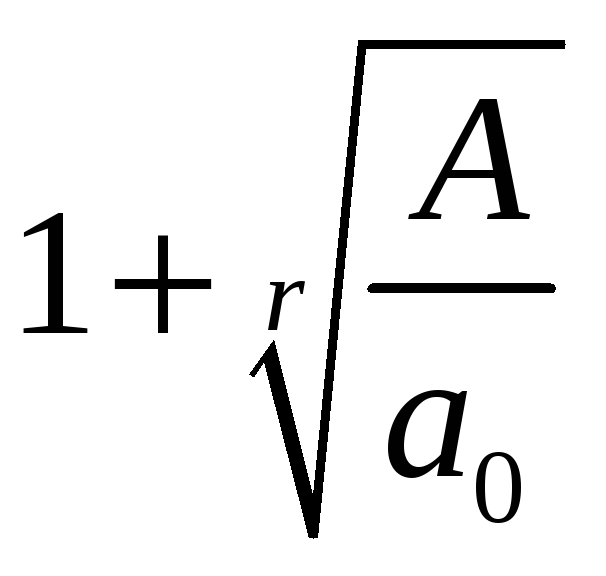(Лагранж),

где А – max из mod отрицательных коэффициентов.

- индекс первого отрицательного коэффициентов.

Теорема №3(Ньютона)

Число а есть верхняя граница положительных корней полинома f(x), если f(a)>0, f’(a)>0,…,

Замечание №1

Чтобы получать оценку снизу, следует … (-1)ⁿ f(-x) и оценить его корни сверху.

Замечание №2

Если все коэффициенты f(x)0, то f(x) не имеет положительных корней.

Упражнение №693

3	1	-4	4		-8		3
3	1	-1	7		4		15
3	1	2	25		34		>0
3	1	5	10		>0
3	1	8	>0
3	1	>0

Пусть , ,

Теорема №4.

Если f(x) имеет корень , то

Упражнение №664(а)

	1	-6	15	-14
1	1	-5	10	-4
2	1	-4	7	0
7	1	1	22	140

Следовательно , т.е. .

И тогда мы делим на x-2. В результате деления мы получим следующее выражение: .

Прировняем его к нулю и решим как квадратное уравнение:

.

Пусть , .

Теорема №5

Если f(x) имеет корень и при этом является несократимой дробью, то:

1) делитель , т.е.

2) p делитель , т.е.

3) p-mq делитель f(m), т.е.

Замечание №3

В частности, ; .

Упражнение 664(а)

	6	19	-7	-26	12
3/2	6	28	35	26,5	51,75
2/3	6	28	8,3	-20,4
4/3	6	27	29	12,6	28,8
½	6	22	4	-24	0
-3	6	4	-8	0

D=4+48=52=4*13;

/

Замечание №4

Если в f(x) , то f(x) можно свести f(x) c .

Замечание №5

Уравнение с целочисленными коэффициентами чаще всего не имеет рациональных корней.

Возвратные полиномы.

Определение №2

называется возвратным, если , , …,, …, по (сравнивать) коэффициенты симметрично относительно середины.

Пример.

- бином.

Обозначим

Утверждение №1

f возвратен тогда и только тогда, когда .

Но , следовательно возвратные полиномы удовлетворяют функциональному соотношению .

Теорема №6

Если n- нечётная, то возвратный полином имеет корень .

Доказательство:

Вычислим Следовательно f(x) нечётной степени можно представить в виде f(x)=(x+1)g(x), где g(x) – возвратный полином чётной степени.

Упражнение №582.

;

Поделим его на х²:

;

Пусть

D=24;

Следовательно

D=

Упражнение №1

Поделим на х³:

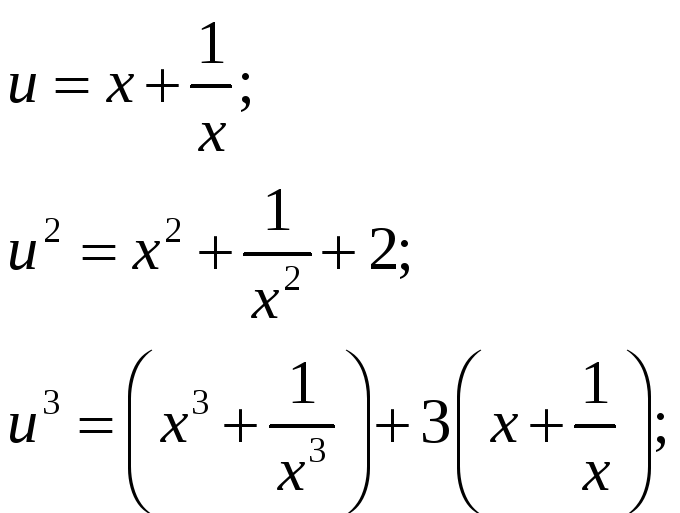
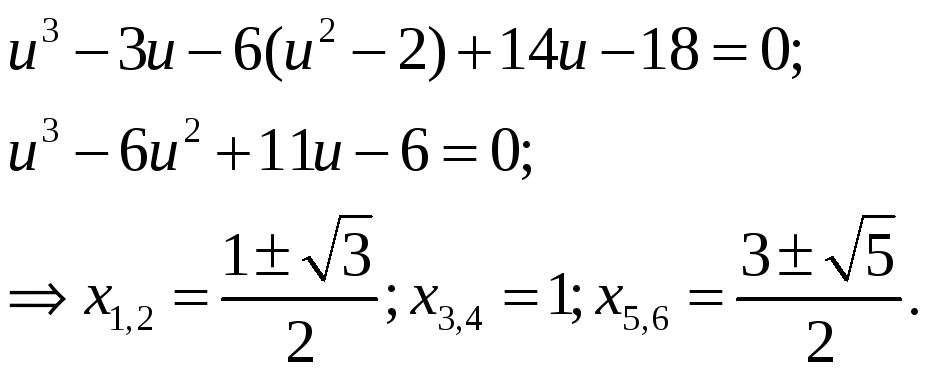
Теорема №7 Признак неприводимости Эйзенштейна.

Пусть p – просто число.

, ;

f не приводим над полем .