Оглавление
Оглавление 1
Занятие 8. Полиномы. Действия над полиномами. Схема Горнера 2
8.1.Полиномы. Определение 2
8.1.Действия над полиномами 2
8.2.Схема Горнера. Вычисление значения полинома в точке 2
8.3.Схема Горнера. Вычисление корней полинома и нахождение полинома степени 3
Занятие 9. Деление полиномов. НОД. Алгоритм Евклида. Линейное представление НОД 6
9.1.Деление полиномов. НОД 6
9.2. Алгоритм Евклида 7
9.3. Линейное представление НОД 7
Занятие 10. разложение полинома по степеням через схему Горнера. Кратные корни. Отыскание кратности корня с помощью схемы Горнера 8
10.1. Формула ТеЙлора, разложение полинома по степеням (через схему Горнера) 8
10.2. Кратность корней. Нахождение кратности корня с помощью схемы Горнера 10
10.2. Способ нахождения всех кратных корней 11
Занятие 9. Решение уравнений 3-й и 4-й степени 13
9.1. Решение уравнений 3-й степени 13
9.2. Решение уравнений 4-й степени 16
Занятие 12. Полиномы над полем . Приводимость. Полиномы над полем 18
12.1. Решение уравнений -й степени 18
Занятие 8. Полиномы. Действия над полиномами. Схема Горнера
-
Полиномы. Определение
Определение 8.1. Многочленом (полиномом) называется функция
Определение 8.2.
Говорят, что полином
имеет степень
n,
если
.
Обозначение:
.
Определение 8.3.
Два полинома
называются тождественно равными,
если
при всех
где
и
.
Теорема 8.1.
Два полинома
тождественно равны
тогда и только тогда, когда выполнены
два условия:
-
Действия над полиномами
Для полинома определяются операции сложения и умножения:
Упражнение 8.1.
Найти многочлены
.
-
Схема Горнера. Вычисление значения полинома в точке
Задача 1.
Как вычислить значение
в точке
наискорейшим образом?
При вычислении «в
лоб», т. е.
,
потребуется
раз возводить в степень, потом n
раз умножать на
и n
раз складывать:
действий. Попробуем считать по-другому:
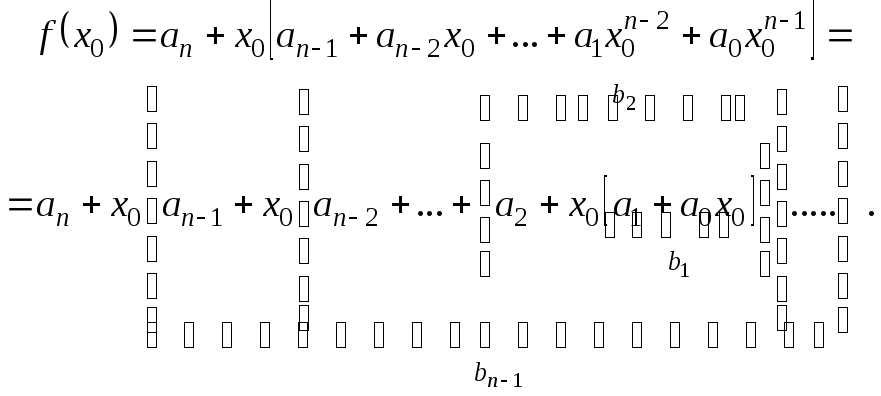
И начинаем вычислять с самой внутренней скобки. Получаем 2n операций. Именно этот алгоритм реализован в схеме Горнера.
где
Легко видеть, что
.
Пример 8.1.
Упражнение 8.2. 544а).
-
Схема Горнера. Вычисление корней полинома и нахождение полинома степени
Основная задача классической высшей алгебры – решение уравнений и систем уравнений. Рассмотрим уравнение
(8.1)
где
Определение 8.4. Уравнение (8.1) называется алгебраическим.
Определение 8.5.
Значение
называется корнем
полинома
(или уравнения (8.1)), если
.
Упражнение 8.3. П
75p),
.
Существует ли у уравнения (8.1) хотя бы один корень?
Теорема 8.2.
(Основная теорема высшей алгебры).
Уравнение (8.1) имеет, по крайней мере,
один корень
,
в общем случае комплексный.
Определение 8.6.
Выражение вида
называется линейным
множителем
для многочлена
.
Теорема 8.3.
(Безу).
Полином
можно представить в виде
где
.
Доказательство.
Пусть
и
.
Тогда
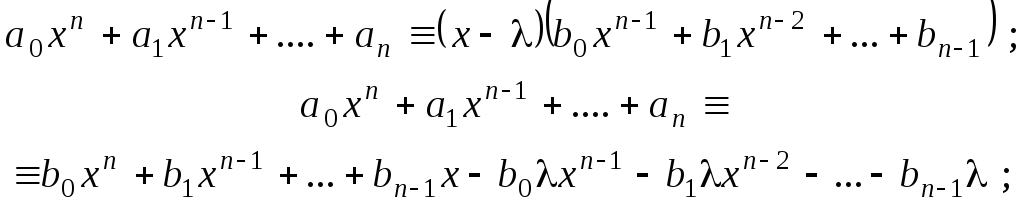
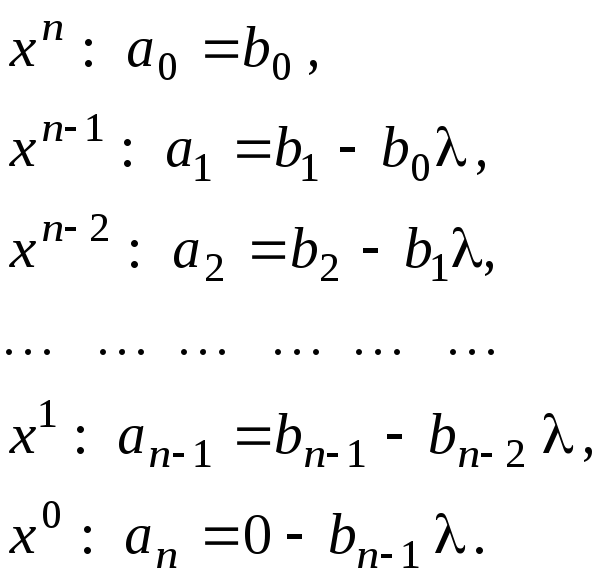
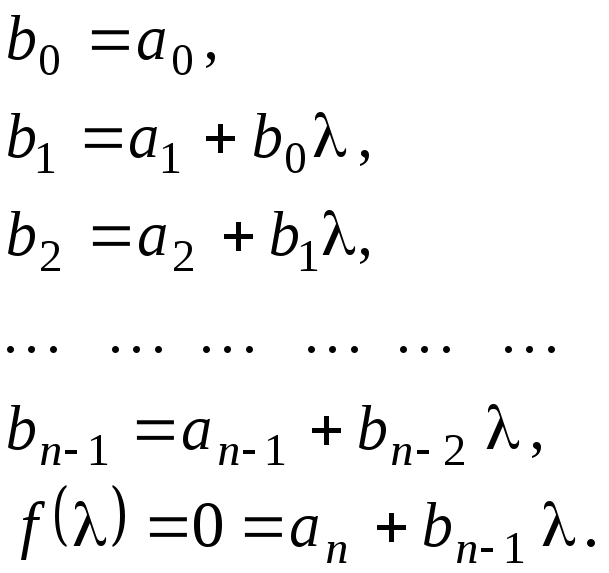
Как видим выражения
для
совпадают с выражениями в первой строке
схемы Горнера
Пример 8.2.
Упражнение 8.4.
Найти
для П 75p),
,
.
Итак, если найден один корень уравнения (8.1), то можно понизить степень на 1 и рассматривать уравнение
Теорема 8.4.
(Следствие
к основной теореме высшей алгебры).
Каждый полином
можно представить в виде
(8.2)
И такое представление единственно.
Определение 8.7. Представление (8.2) называется разложением полинома на линейные множители.
Пример 8.3.
В П 75p)
разложить
на линейные множители. В П 75p)
такое представление
(как видим в таком представлении могут встречаться и одинаковые линейные множители)
Упражнение 8.5. П 582 d).
Теорема 8.5. (Виета). Пусть корни многочлена
равны
,
тогда
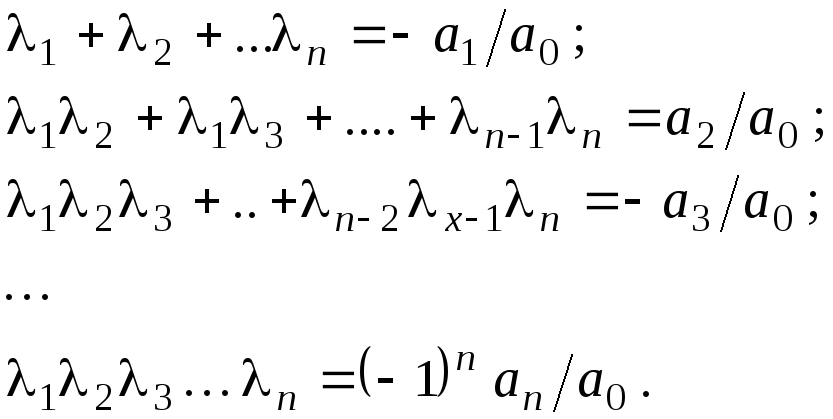
Пример 8.4.
Д/з: 544 b), 582, 618, 624 (а, b), 626.
Занятие 9. Деление полиномов. НОД. Алгоритм Евклида. Линейное представление НОД
-
Деление полиномов. НОД
Теорема
9.1. (О делении с остатком). Для
полиномов
и
существуют
и единственны
полиномы
и
,
такие что:
где
.
Упражнение 9.1. П 539 а).
Имеется полная аналогия между множеством целых чисел и множеством полиномов.
Определение 9.1.
Пусть
.
Тогда
называется общим
делителем
.
Определение 9.2. НОД – полином наибольшей степени из бесконечного множества общих делителей.
9.2. Алгоритм Евклида
Как найти НОД?
-
Разложить оба многочлена на линейные множители.
Упражнение 9.2. П 588 а).