РАБОЧАЯ ТЕТРАДЬ

ПО МАТЕМАТИЧЕСКОЙ

СТАТИСТИКЕ

Студента ____________________________

(Фамилия И.О.)

Группа _________

Вариант № ________

Оценка ________________________

Преподаватель__________________

Оценка ________________________

Преподаватель__________________

План выполнения типового расчёта

1. Построение статистического распределения выборки.

2. Вычисление точечных оценок математического ожидания и дисперсии.

3. Построение гистограммы относительных частот.

4. Проверка гипотезы о нормальном распределении случайной величины.

5. Нахождение доверительных интервалов для математического ожидания и дисперсии.

6. Решение дополнительной задачи.

Перед началом выполнения типового расчёта по математической статистике повторите (или изучите) следующие темы.

1. Дискретные случайные величины. Закон распределения вероятностей дискретной случайной величины. Числовые характеристики дискретной случайной величины.

2. Непрерывные случайные величины. Функция распределения, плотность распределения, их взаимосвязь и свойства. Нормальный закон распределения непрерывных случайных величин, правило «трех сигм». Числовые характеристики непрерывных случайных величин.

3. Генеральная совокупность и выборка. Вариационный ряд. Гистограмма, эмпирическая функция распределения выборки.

4. Статистическое оценивание параметра распределения по выборке. Точечные оценки и их характеристики: несмещённость, эффективность, состоятельность.

5. Интервальные оценки. Доверительные интервалы. Интервальное оценивание параметров нормального распределения.

6. Статистические гипотезы, их виды. Понятие о проверке статистических гипотез. Ошибки 1-го и 2-го рода. Критерий согласия Пирсона.

1. Построение статистического распределения выборки

Данную выборку преобразуйте в вариационный (интервальный) ряд. Для этого:

1. Упорядочите выборку, т.е. запишите все значения случайной величины в возрастающем порядке. Если какое-либо значение повторяется, запишите его столько раз, сколько оно Вам встретилось.

2. Вычислите объем выборки ; минимальное значение ; максимальное значение .

3. Разбейте диапазон изменения случайной величины на интервалы. Число интервалов определяется по формуле с округлением до ближайшего целого: .

Ширину каждого интервала выберите с точностью выборки и округлите в сторону завышения .

Границы интервалов вычислите по формулам , .

; ; ;

;;;

;; .

4. Вычислите частоту каждого интервала – количество элементов , попавших в -й интервал. Если элемент совпадает с границей интервала, то он относится к интервалу с меньшим порядковым номером.

5 Вычислите относительные частоты интервалов по формулам .

Полученные данные занесите в четыре первые столбца таблицы 1.

2. Вычисление точечных оценок математического ожидания и дисперсии

Оценки математического ожидания и дисперсии вычисляются по формулам 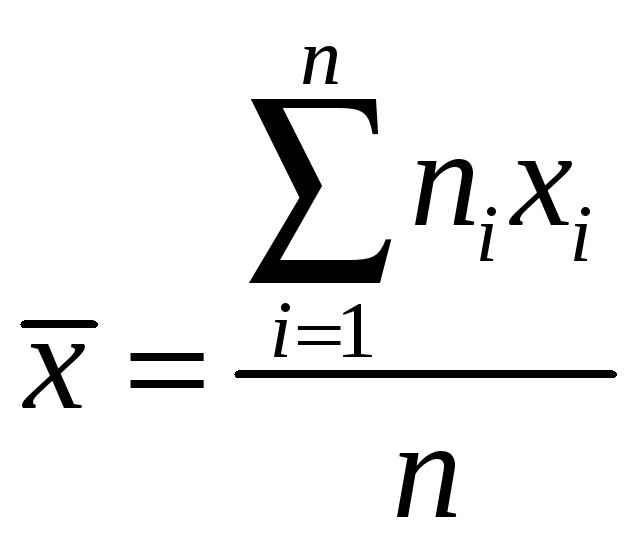, , 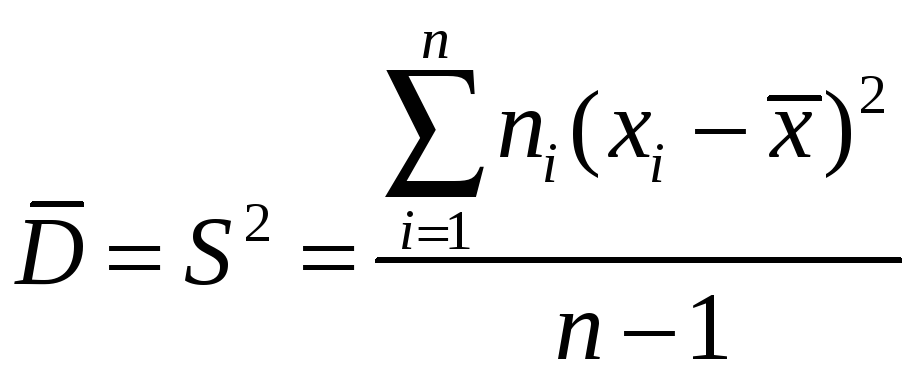где – частота варианты , – объём выборки.

Если объем выборки велик, то вычисление точечных оценок математического ожидания и дисперсии по этим формулам громоздко. Для сокращения вычислений элементам выборки, попавшим в -й интервал, припишем значения, равные серединам интервалов: .

Внесите полученные значения в пятый столбец таблицы 1.

Далее варианты замените на условные варианты по формулам , где – так называемый ложный нуль (новое начало отсчета).

Ложный нуль находим по следующему правилу:

– если число интервалов нечетное, то = середине среднего интервала,

– если число интервалов четное, то = середине того интервала, у которого больше частота .

При этом варианте, которая принята в качестве ложного нуля, соответствует условная варианта, равная нулю.

Значения внесите в таблицу 1.

Вычислите произведения , результаты занесите в таблицу 1.

Суммируя седьмой столбец таблицы 1, вычислите значение .

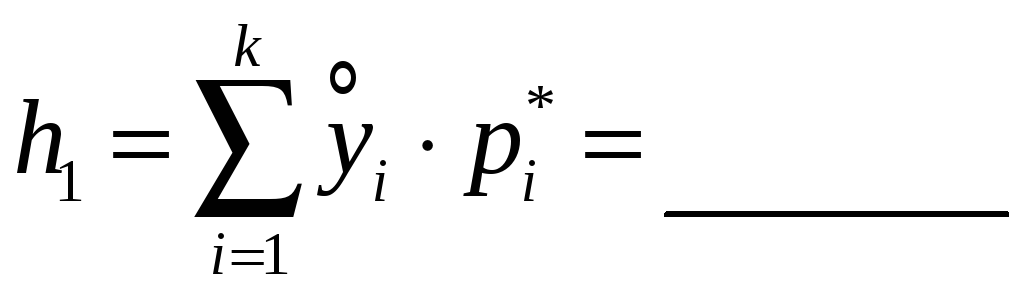Вычислите оценку математического ожидания по формуле .

.

Вычислите произведения , результаты занесите в таблицу 1.

Суммируя восьмой столбец таблицы 1, вычислите значение .

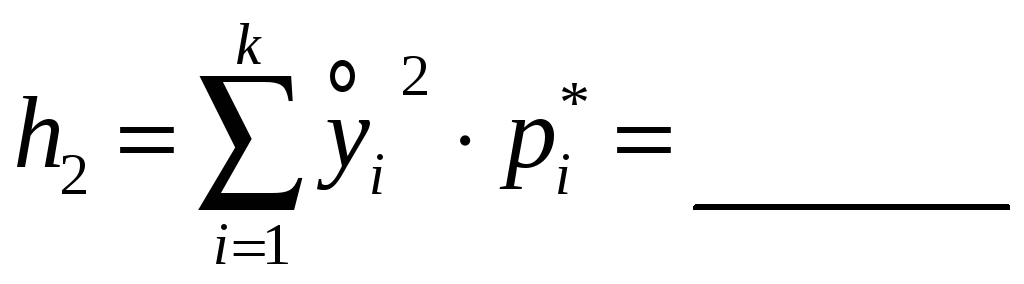Вычислите оценку дисперсии по формуле .

Оценка занижает дисперсию генеральной совокупности, поэтому введя поправочный коэффициент , получим несмещенную оценку дисперсии .

Вычислите оценку среднего квадратического отклонения

.

Таблица 1

№	Границы интервалов
1	2	3	4	5	6	7	8	9
1
2
3
4
5
6
7
8
Σ						h1=	h2=

Для сравнения вычислите по «правилу ».

Так как для случайной величины, имеющей нормальное распределение, почти все значения укладывается на симметричном относительно математического ожидания участке длиной , то с помощью «правила » можно ориентировочно определить оценку среднего квадратического отклонения нормально распределённой случайной величины. Берем максимальное практически возможное отклонение от среднего значения и делим его на три.

; .

.
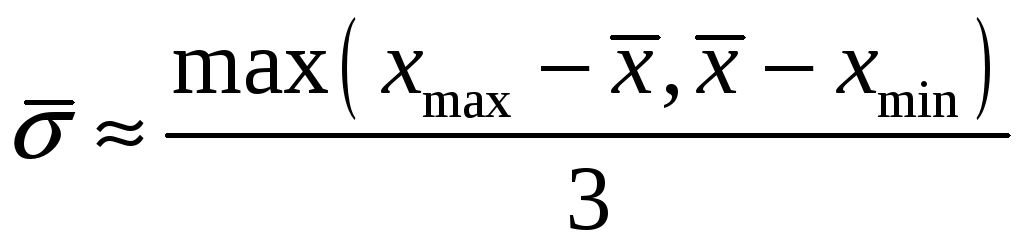